More population genetics… Here, I wanted to look at the process of fixation, that is the process by which a mutant allele comes to take over the entire population. There is a very classic result by Kimura that the chance of fixation depends on population frequency p and the product of the effective population size N and the selective advantage of the mutant allele s, such that

for diploid populations and

for haploid populations. This result is most commonly used to gauge the likelihood that a new mutant entering the population at 1/2N or 1/N frequency will fix.

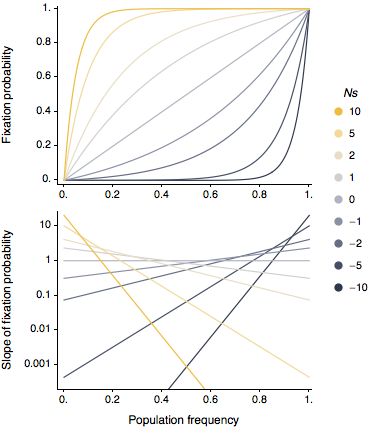
Here, I’m showing the chance that a polymorphism fixes in a haploid population as a function of its frequency in the population p and its scaled selection advantage (or disadvantage) Ns. You can see that when Ns = 0, the chance of fixation is just equal to the mutant’s frequency. If an neutral allele is at 50% frequency in the population, it has a 50% chance of fixing. If a mutation is selectively advantageous, it has a greater chance of fixing than expected from its frequency alone, and likewise, if a mutation is deleterious, it will fix less often than expected from its frequency. A decently advantageous mutant (Ns = 10) is subject to random loss when it’s at low frequency, but will almost certainly fix if it gets to moderate frequency in the population. If it gets to just 3.5% frequency in the population, then it will have a 50% chance of fixing. Conversely, a decently deleterious mutant (Ns = -10) needs to get to high frequency before it has any chance at all of fixing. If it gets to 96.5% frequency, then it will have a 50% chance of fixing.

What’s really striking to me, is that this makes it clear that there’s a snowball effect for advantageous mutants, where getting to some low frequency helps them to get to higher frequency, which in turns helps them to get to even higher frequency and eventually fix. This can be seen as a decreasing slope of the chance of fixation as frequency increases. Every step toward fixation is progressively easier for advantageous alleles. On the other hand, deleterious mutants face an uphill battle. Getting to low frequency is relatively easy, but every step past this gets more and more difficult. This can be seen as in increasing slope as allele frequency increases. Every step toward fixation is progressively harder for deleterious alleles.