Virus evolution, fitness and forecasting
Trevor Bedford
Fred Hutchinson Cancer Center / Howard Hughes Medical Institute
8 Oct 2024
KITP Workshop on Interactions and Co-evolution between Viruses and Immune Systems
University of California Santa Barbara
Slides at: bedford.io/talks
Genetic relationships of globally sampled SARS-CoV-2 to present
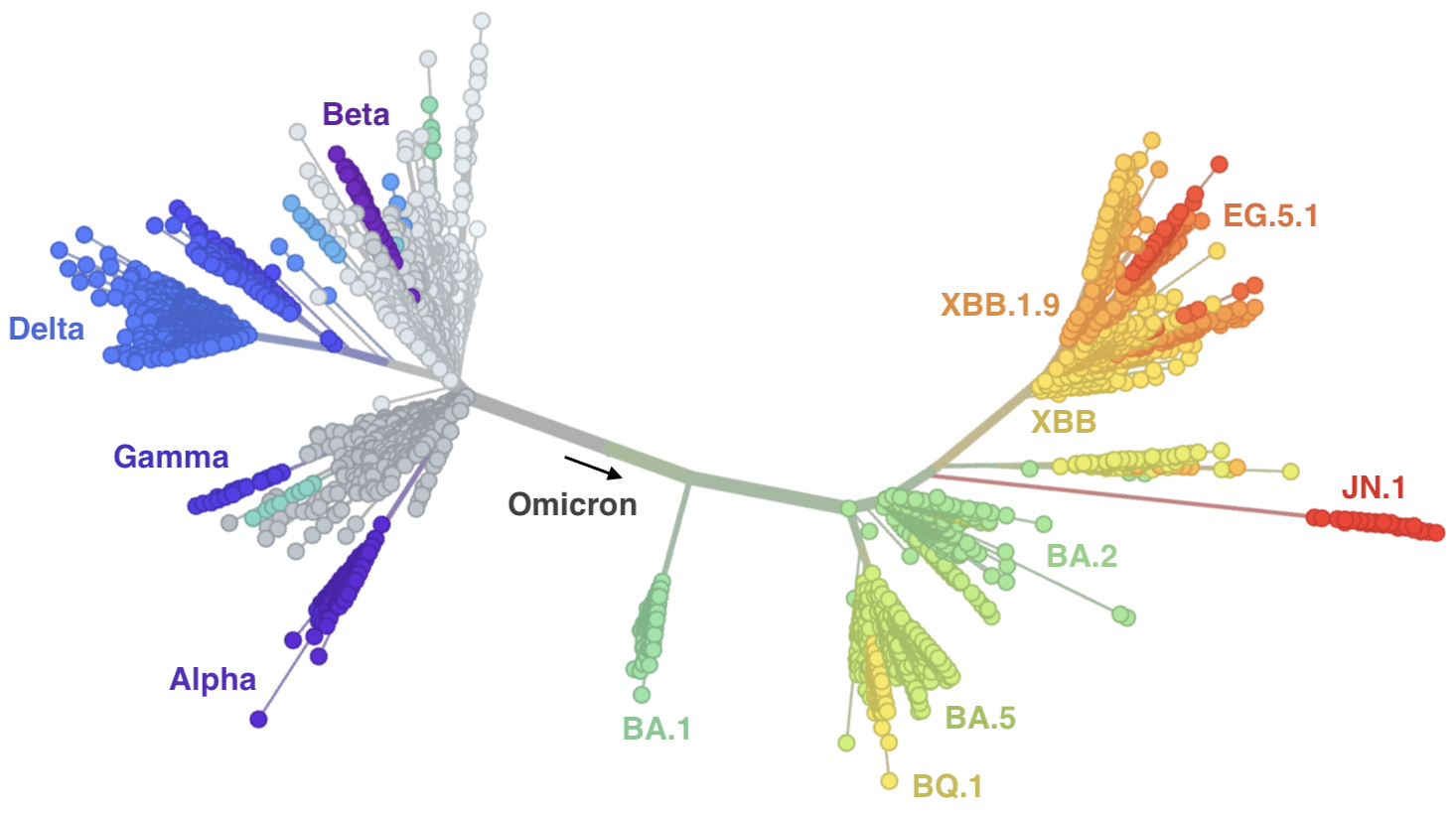
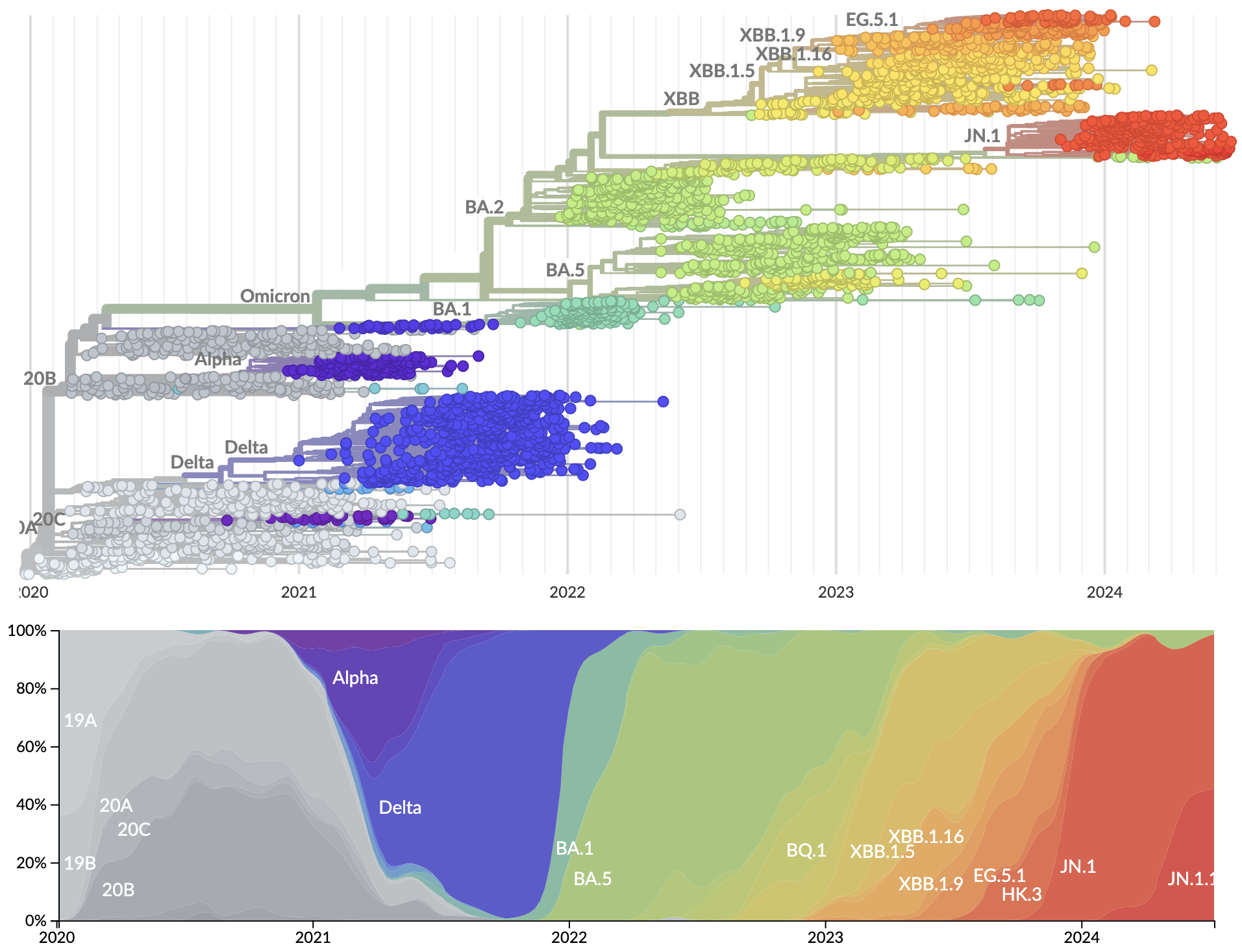
Rapid displacement of existing diversity by emerging variants
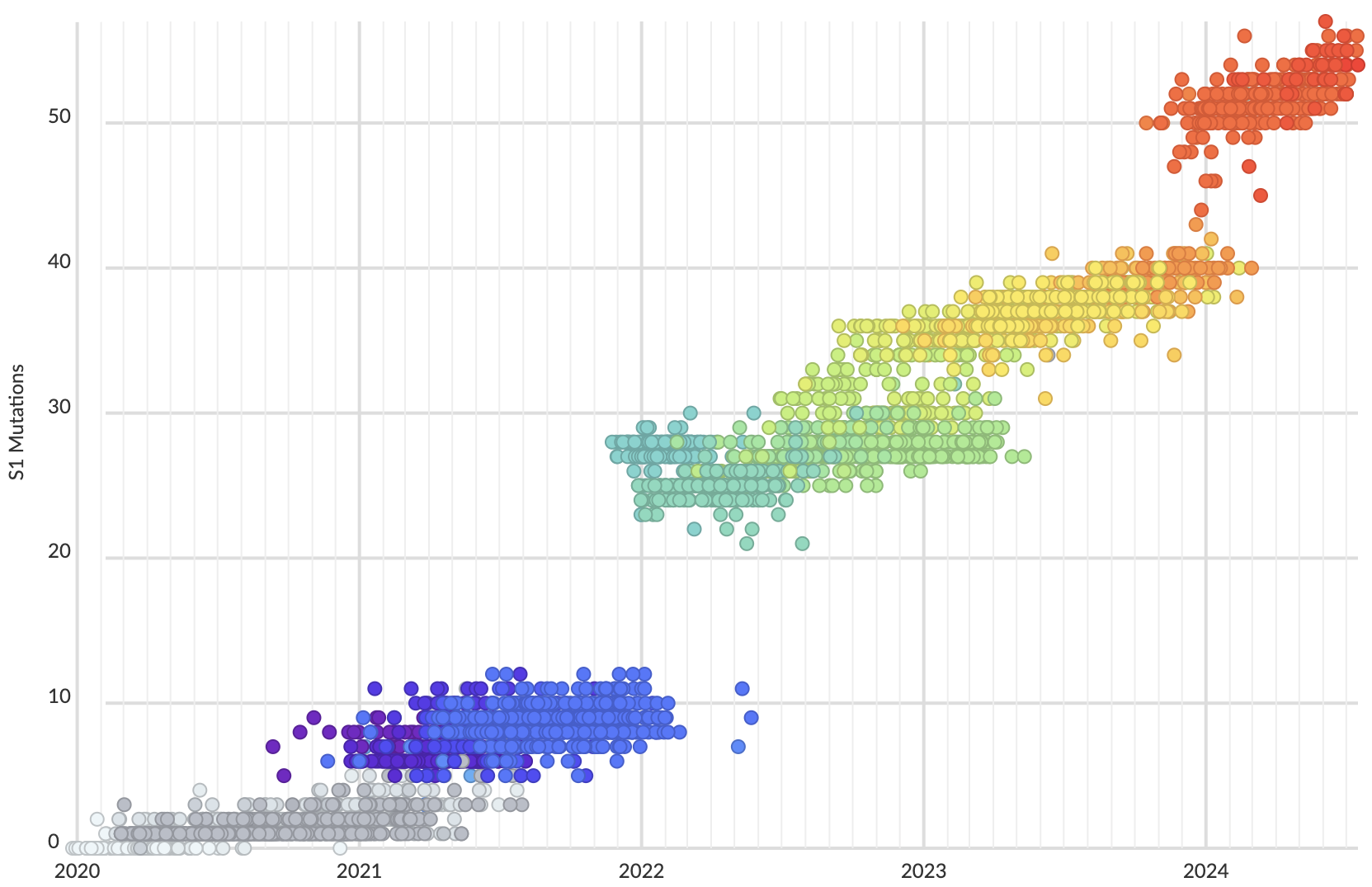
Mutations in S1 domain of spike protein driving displacement
This talk
- Evolutionary patterns across endemic human viruses
- Frequency dynamics and fitness estimation
- Evolutionary forecasting
Evolutionary patterns across endemic human viruses
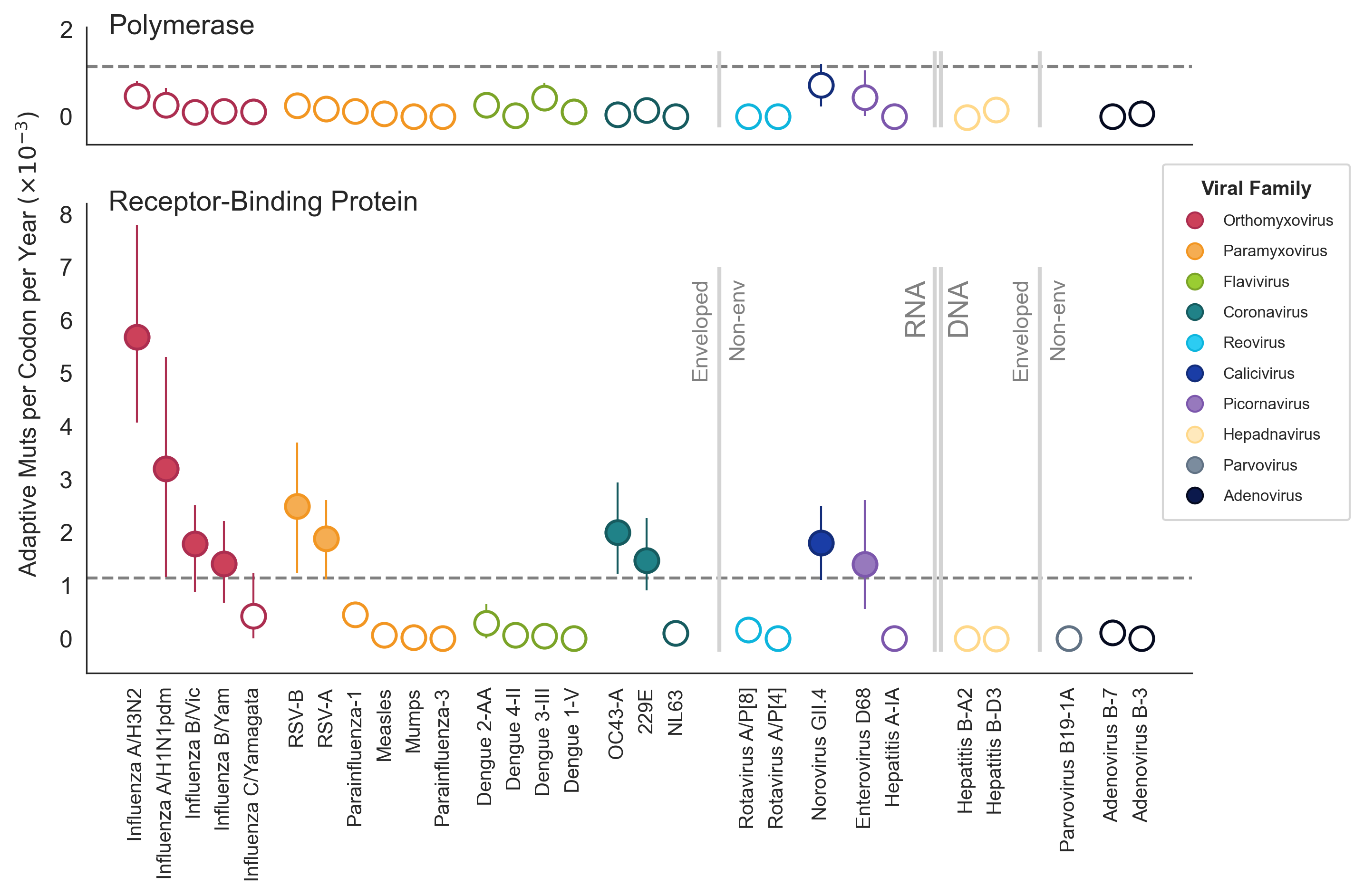
Calculate rates of adaptive evolution across the genomes of 28 endemic human viruses spanning enveloped / non-enveloped and RNA / DNA viruses
Calculate the rate of fixation events through time
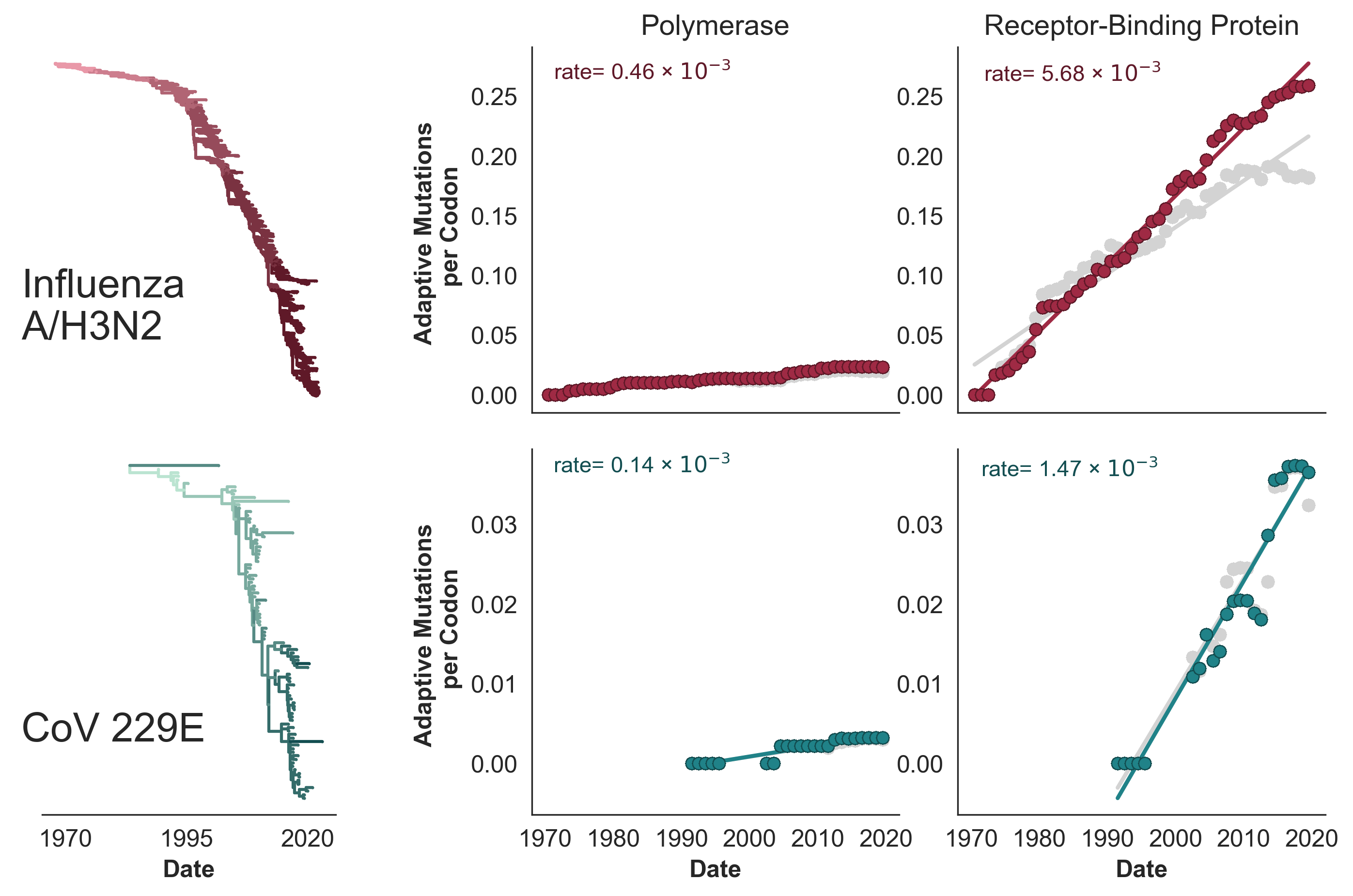
A subset of viruses show adaptive evolution in their surface-located receptor-binding proteins
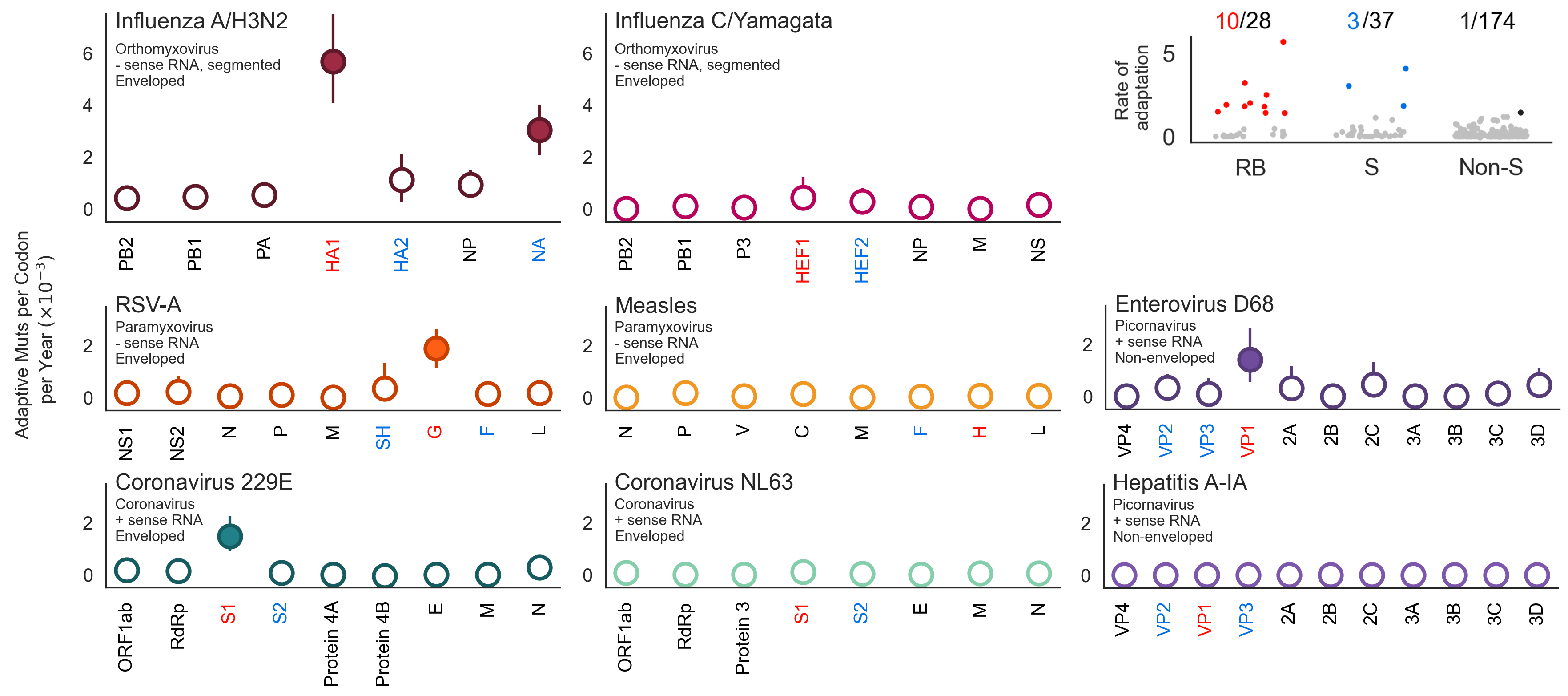
Flu H3N2 is unusually fast, but flu B-like rates are not uncommon
SARS-CoV-2 evolution fast relative to previous endemic viruses
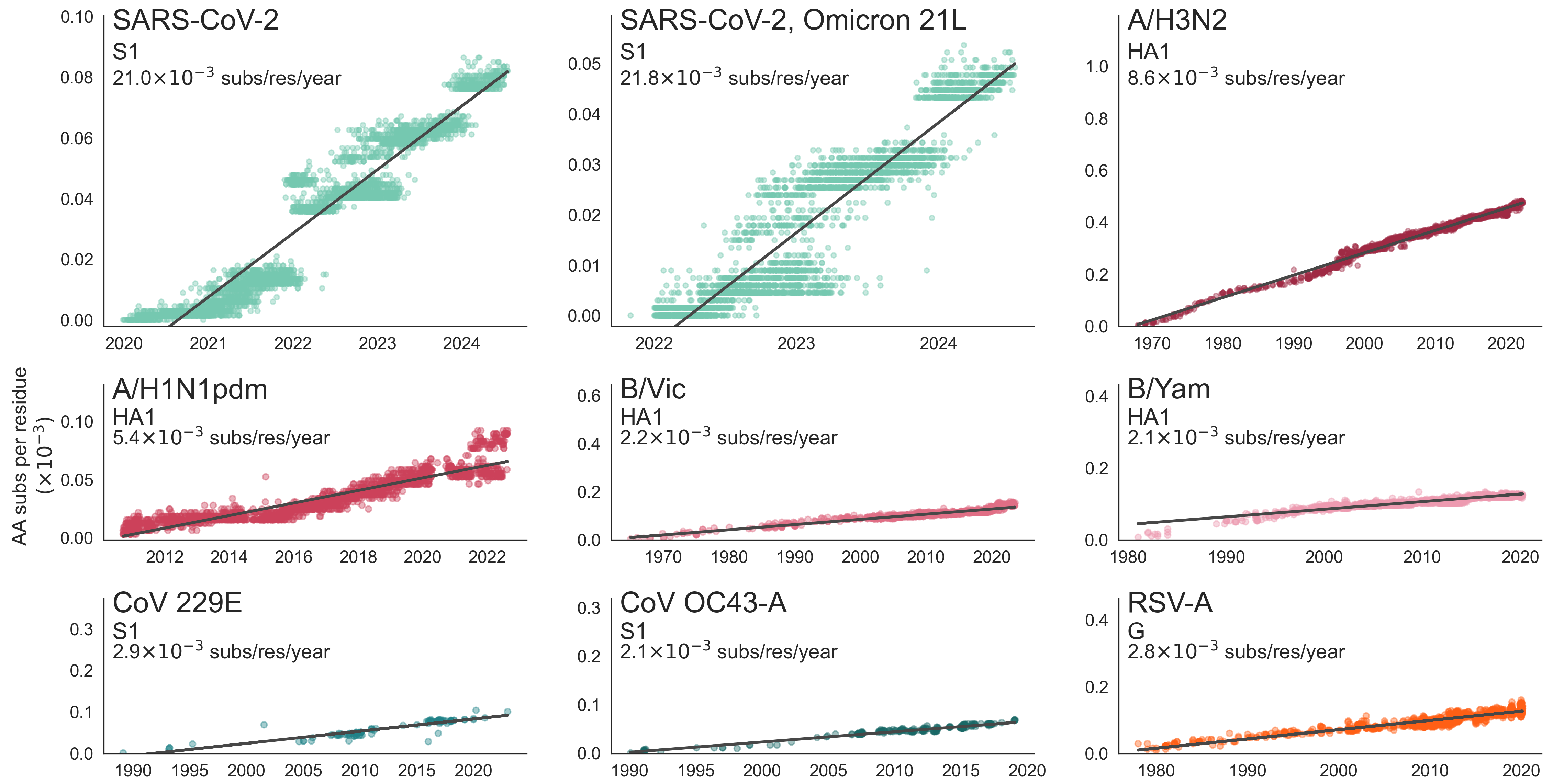
Were transmission enhancing / immune escape variants predictable from spike protein structure or SARS-CoV-2 biology?
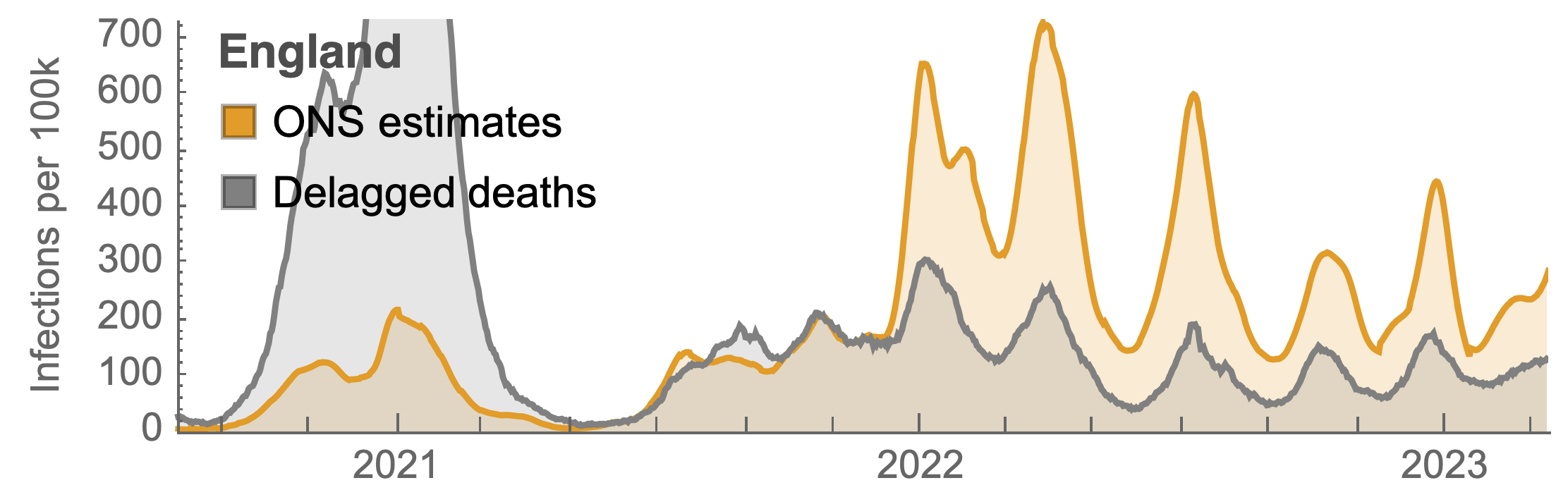
Rapid evolution of SARS-CoV-2 drives high levels of incidence
ONS Infection Survey provides rare source of ground truth, roughly 1 in 3 infections detected in 2021, while 1 in 40 in 2023
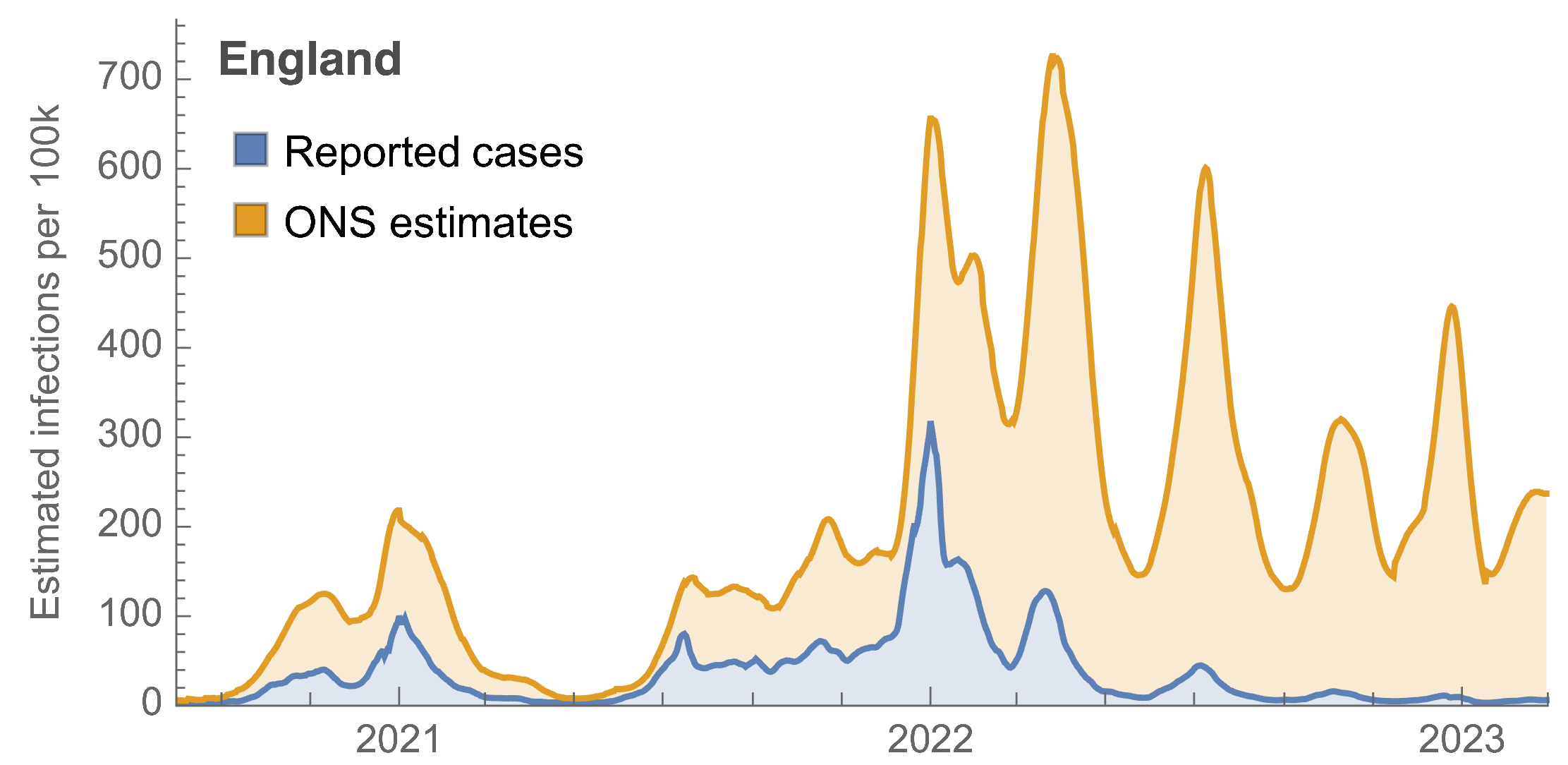
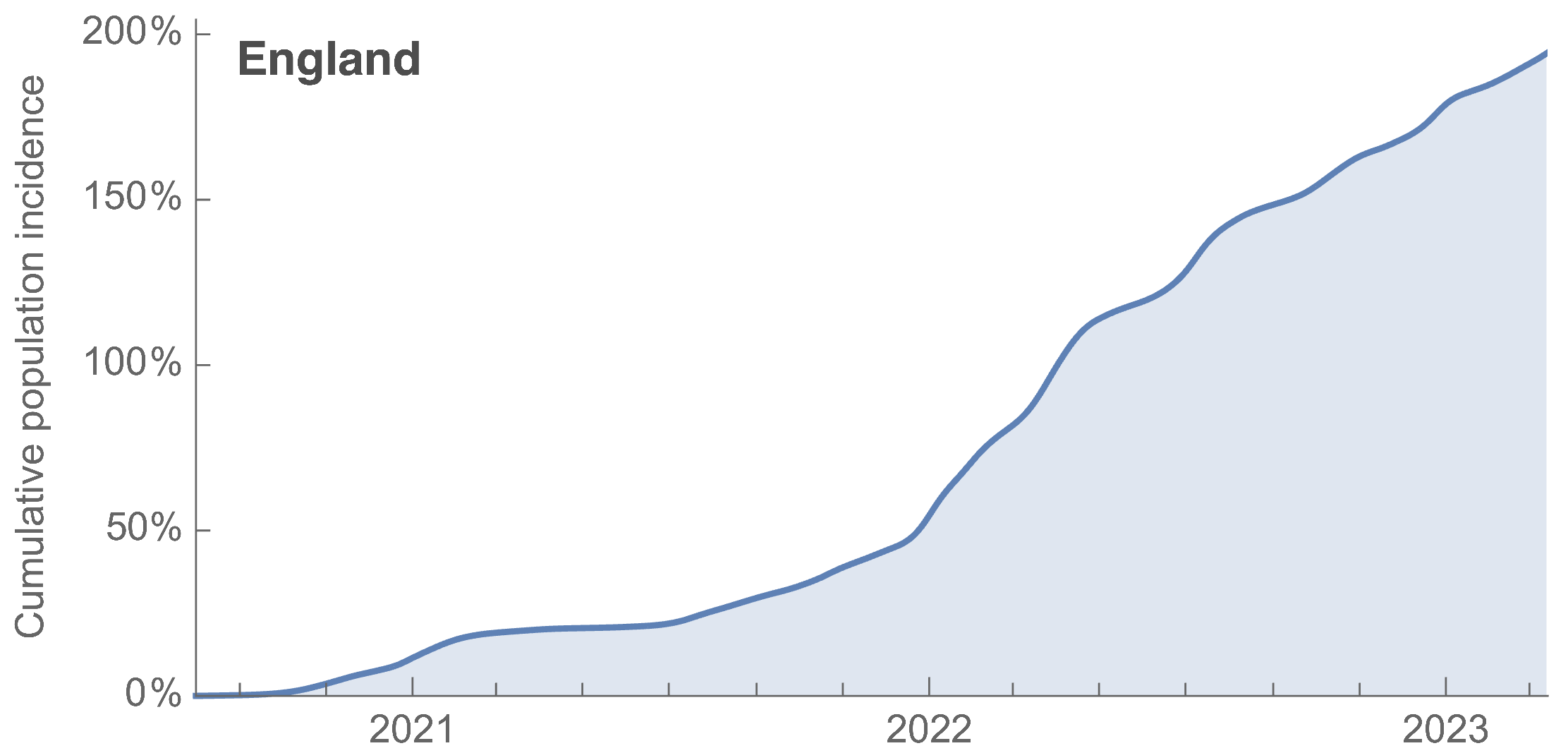
~110% population attack rate from March 2022 to March 2023
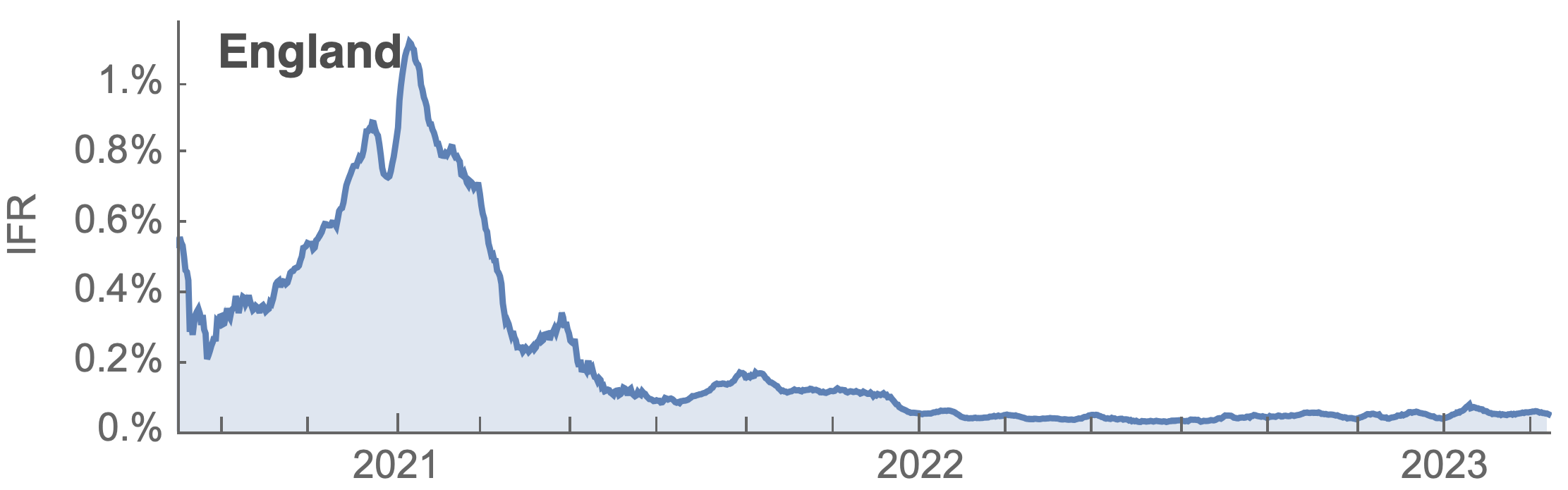
Post-Omicron period shows consistent IFR of 0.04%
Frequency dynamics and fitness estimation
Fitness models to project strain frequencies
Future frequency $x_i(t+\Delta t)$ of strain $i$ derives from strain fitness $f_i$ and present day frequency $x_i(t)$, such that
$$x_i(t+\Delta t) = \frac{1}{Z(t)} \, x_i(t) \, \mathrm{exp}(f_i \, \Delta t)$$
Strain frequencies at each timepoint are normalized by total frequency $Z(t)$. Strain fitness $f_i$ is estimated from viral attributes (primarily number of epitope and non-epitope mutations).
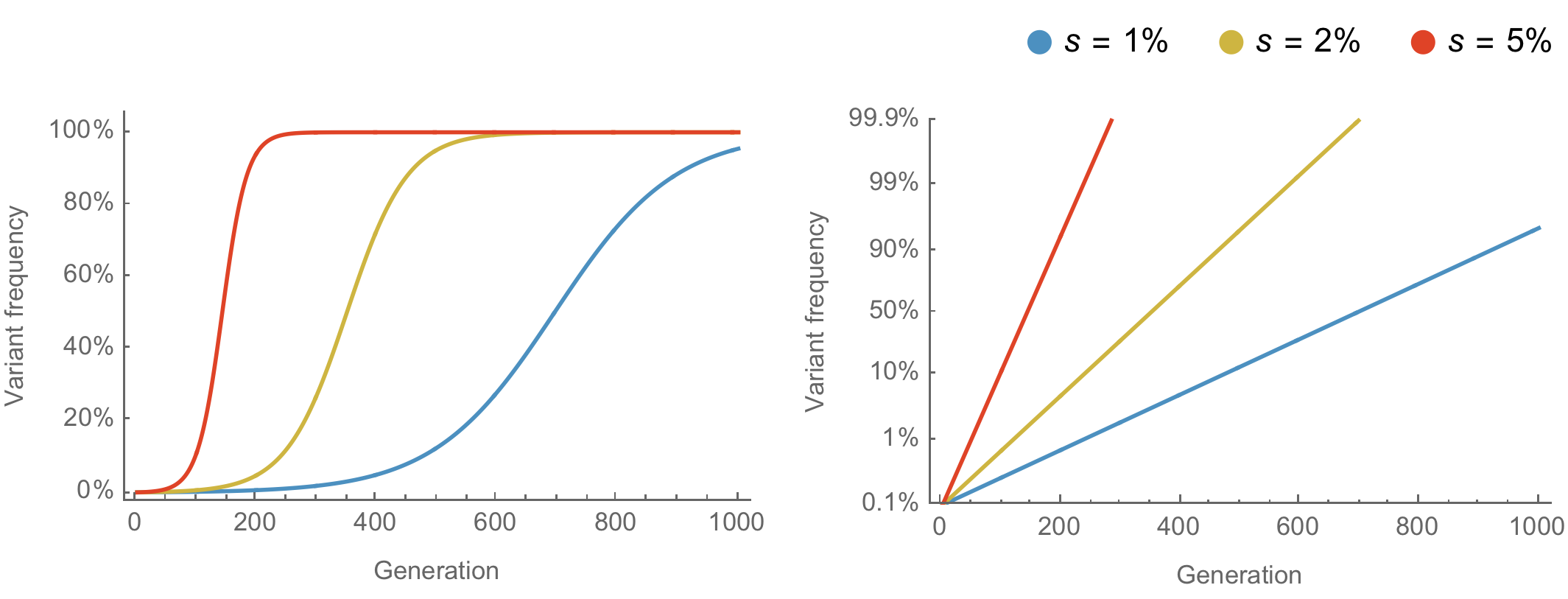
Population genetic expectation of variant frequency under selection
$x' = \frac{x \, (1+s)}{x \, (1+s) + (1-x)}$ for frequency $x$ over one generation with selective advantage $s$
$x(t) = \frac{x_0 \, (1+s)^t}{x_0 \, (1+s)^t + (1-x_0)}$ for initial frequency $x_0$ over $t$ generations
Trajectories are linear once logit transformed via $\mathrm{log}(\frac{x}{1 - x})$
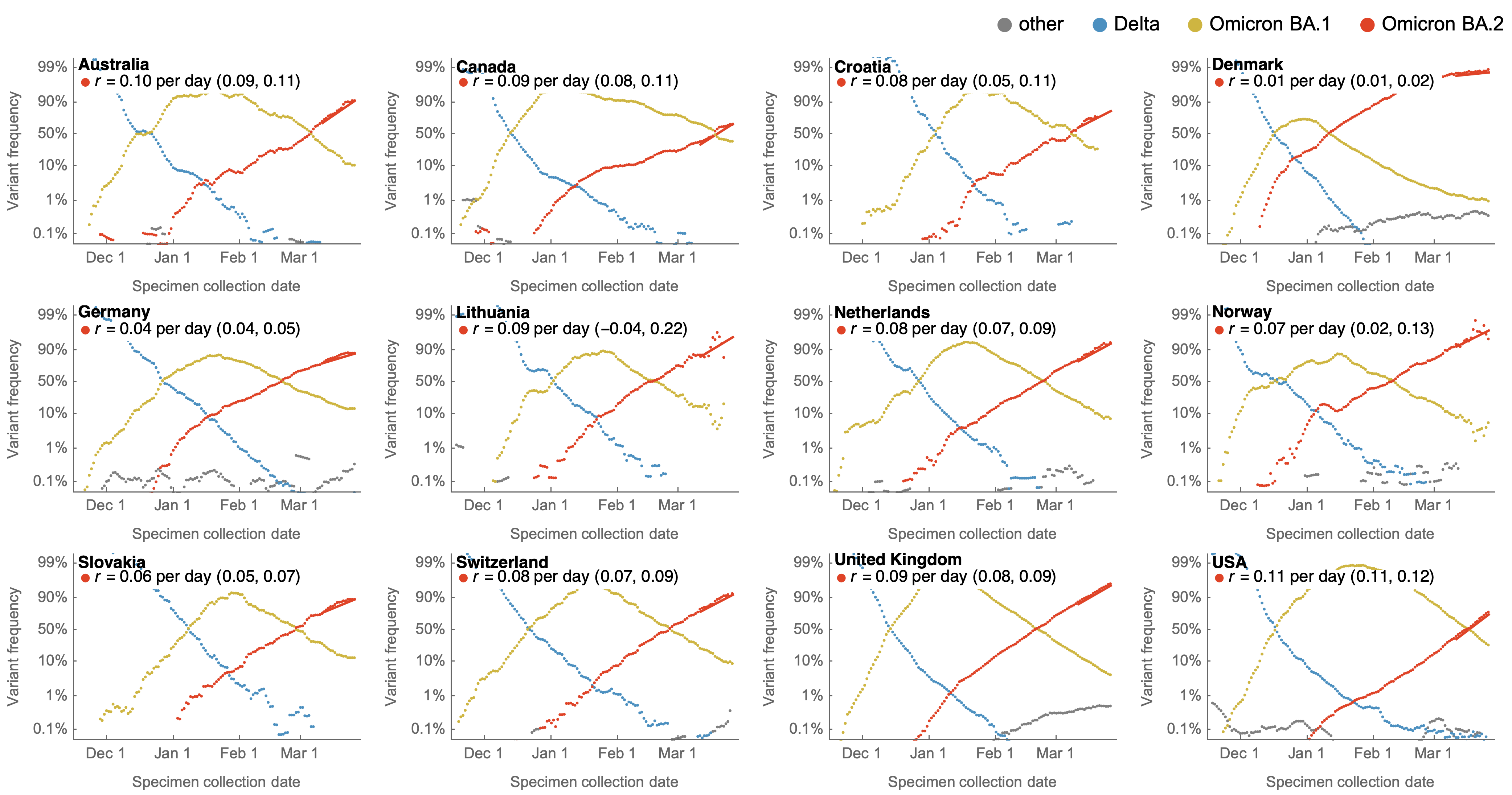
Consistent frequency dynamics in logit space (BA.2 Mar 2022)
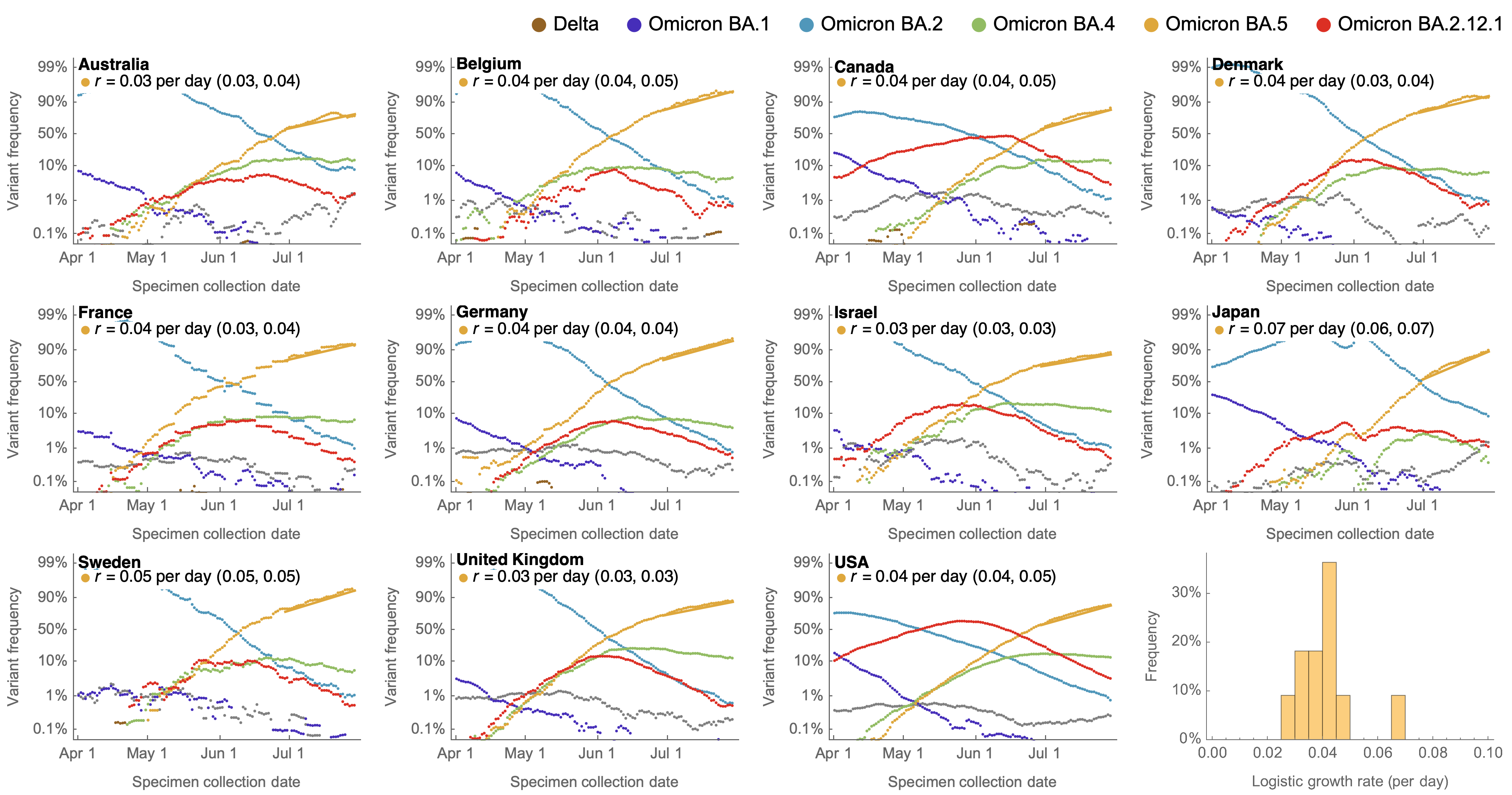
Consistent frequency dynamics in logit space (BA.5 Jul 2022)
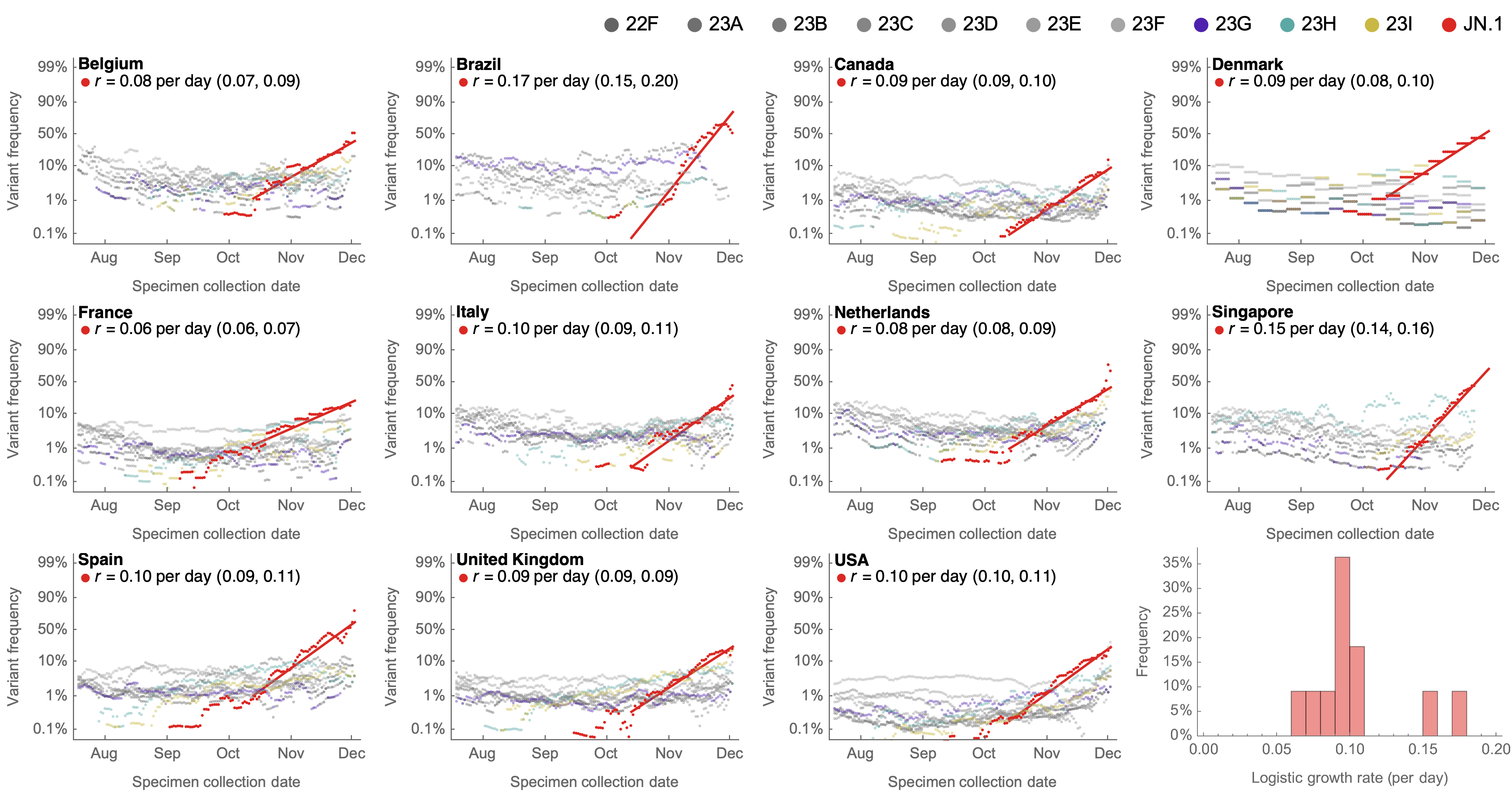
Consistent frequency dynamics in logit space (JN.1 Dec 2023)
Multinomial logistic regression
Multinomial logistic regression across $n$ variants models the probability of a virus sampled at time $t$ belonging to variant $i$ as
$$\mathrm{Pr}(X = i) = x_i(t) = \frac{p_i \, \mathrm{exp}(f_i \, t)}{\sum_{1 \le j \le n} p_j \, \mathrm{exp}(f_j \, t) }$$
with $2n$ parameters consisting of $p_i$ the frequency of variant $i$ at initial timepoint and $f_i$ the growth rate or fitness of variant $i$.
Various flavors of MLR implemented in evofr package
location variant date sequences Japan 22B 2023-02-10 242 Japan 22B 2023-02-11 56 Japan 22B 2023-02-12 70 Japan 22E 2023-02-10 80 Japan 22E 2023-02-11 21 Japan 22E 2023-02-12 27 USA 22B 2023-02-10 41 USA 22B 2023-02-11 23 USA 22B 2023-02-12 23 USA 22E 2023-02-10 368 USA 22E 2023-02-11 236 USA 22E 2023-02-12 246 ...
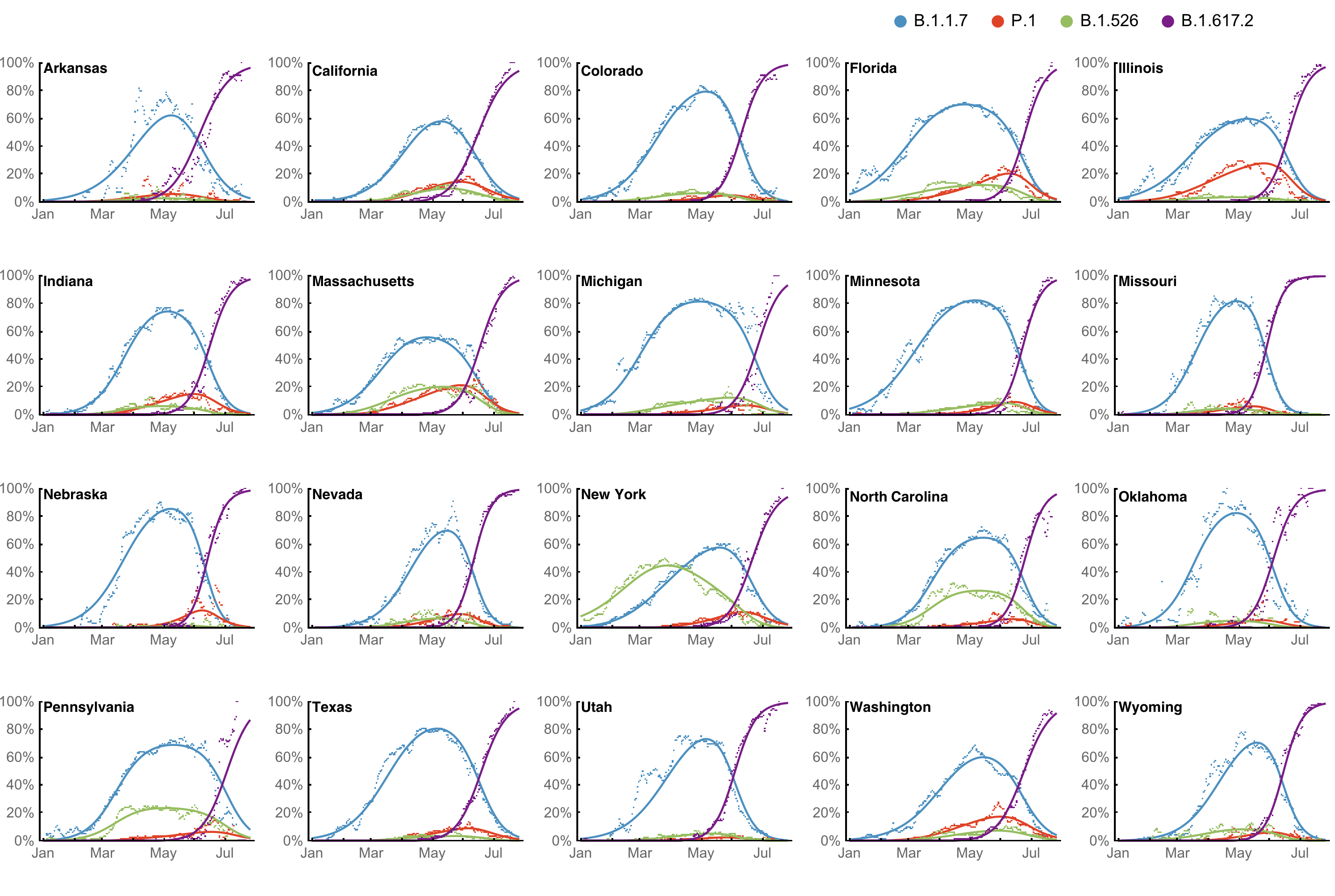
Multinomial logistic regression fits variant frequencies well
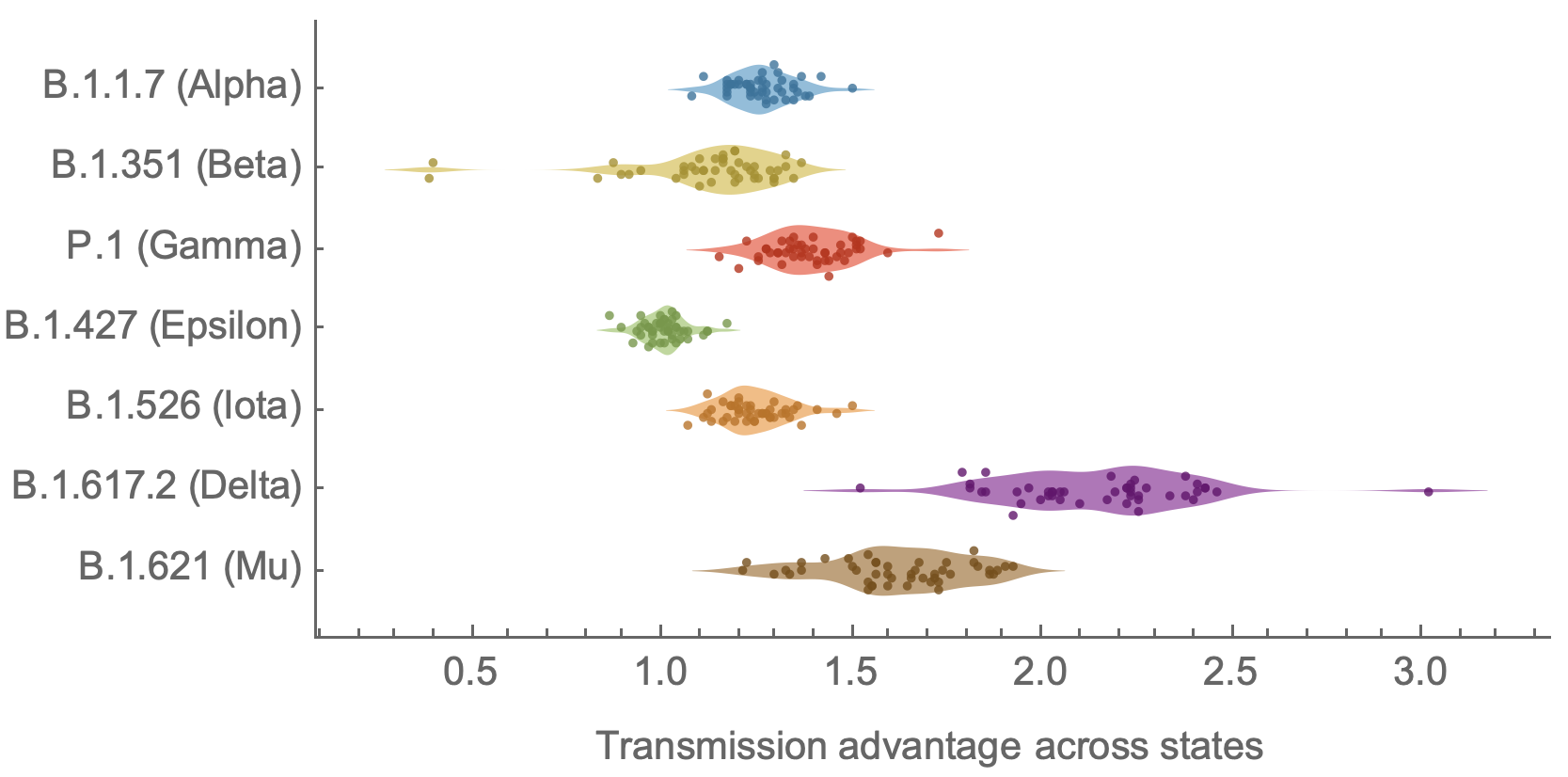
Original VOC viruses had substantially increased transmissibility
Model from Figgins and Bedford. 2022. medRxiv.
Clade-level frequency dynamics and MLR fits in sliding windows
Constant clade fitness within each window, USA data only, ignoring within-clade fitness variation
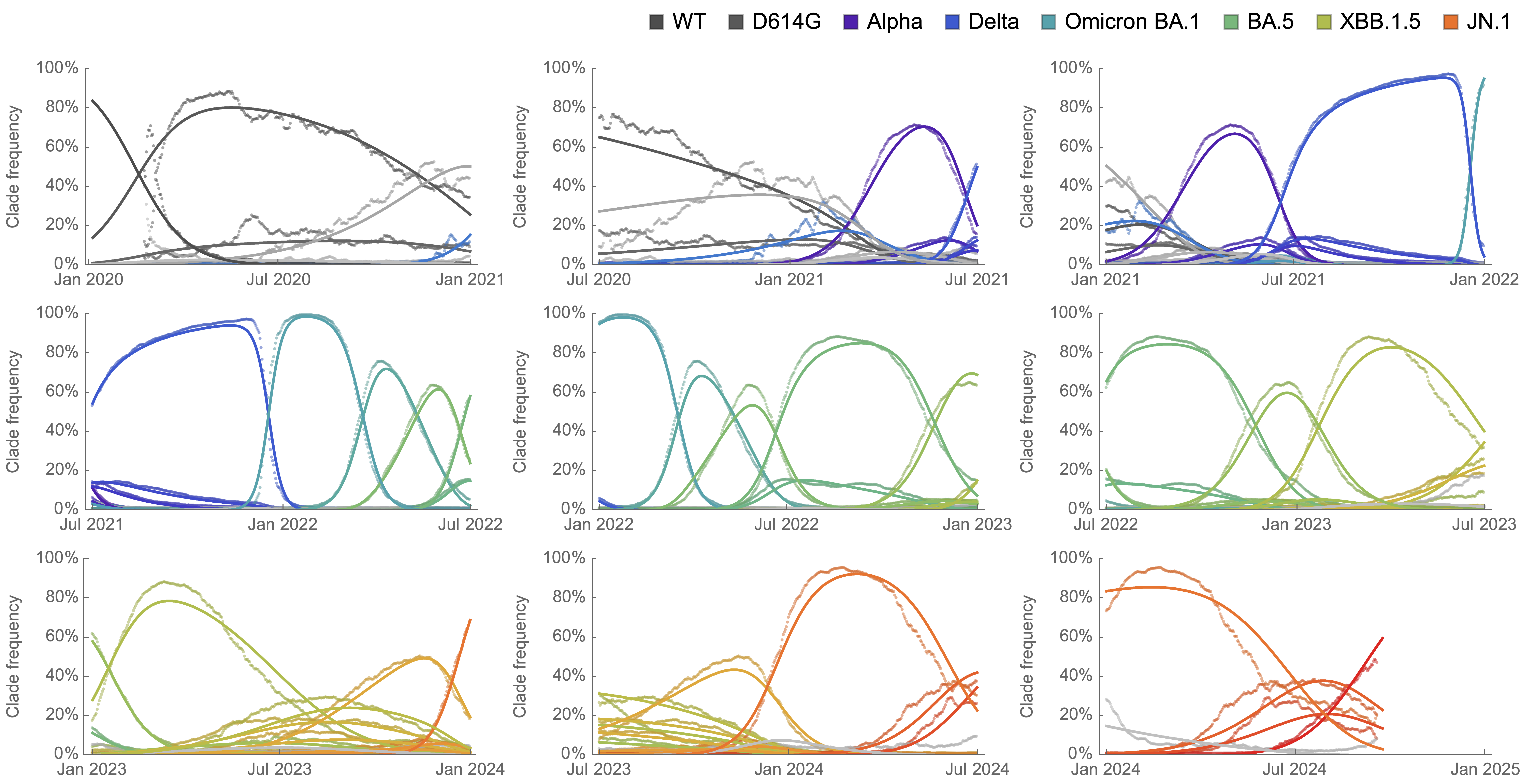
Over the past >4 years, SAR-CoV-2 roughly doubled in fitness every year
Line thickness is proportional to variant frequency
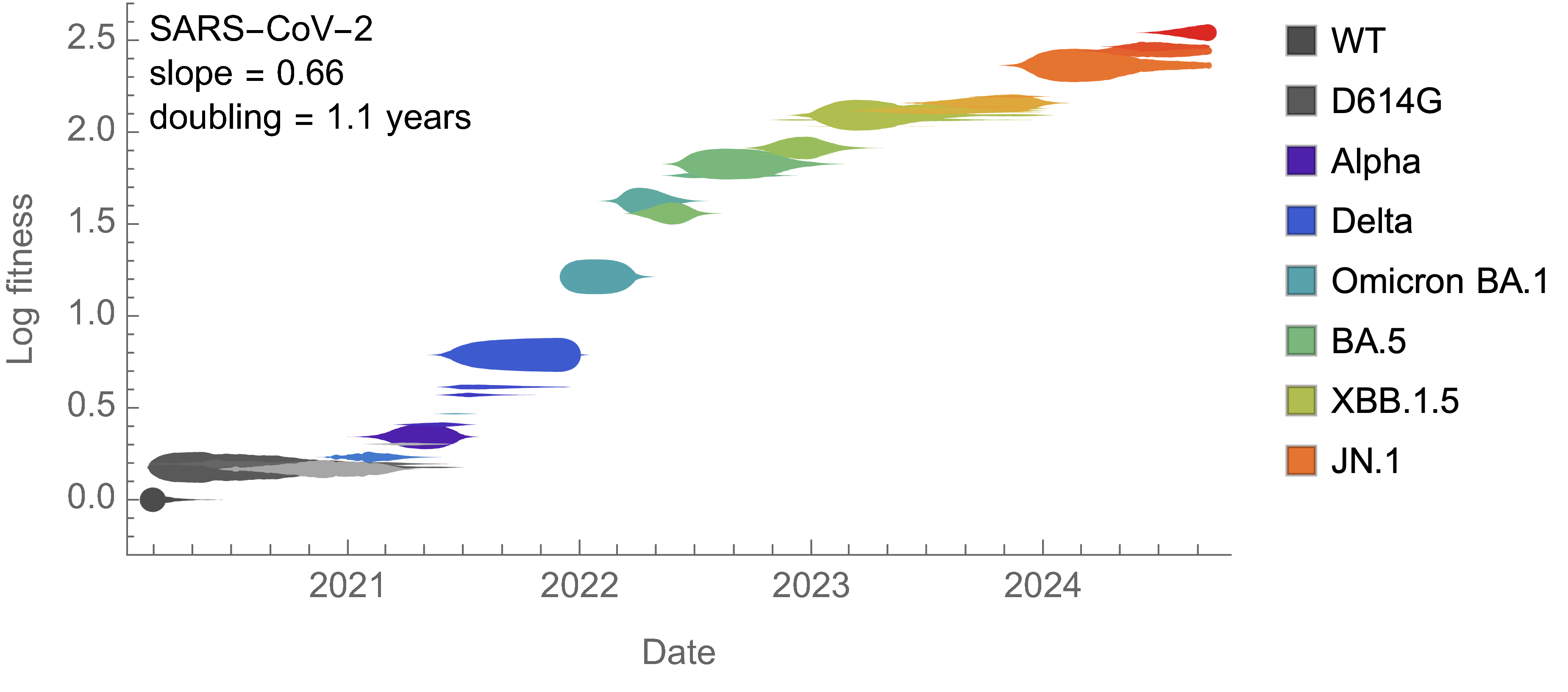
On average, SARS-CoV-2 accumulated 13-14 spike S1 mutations every year
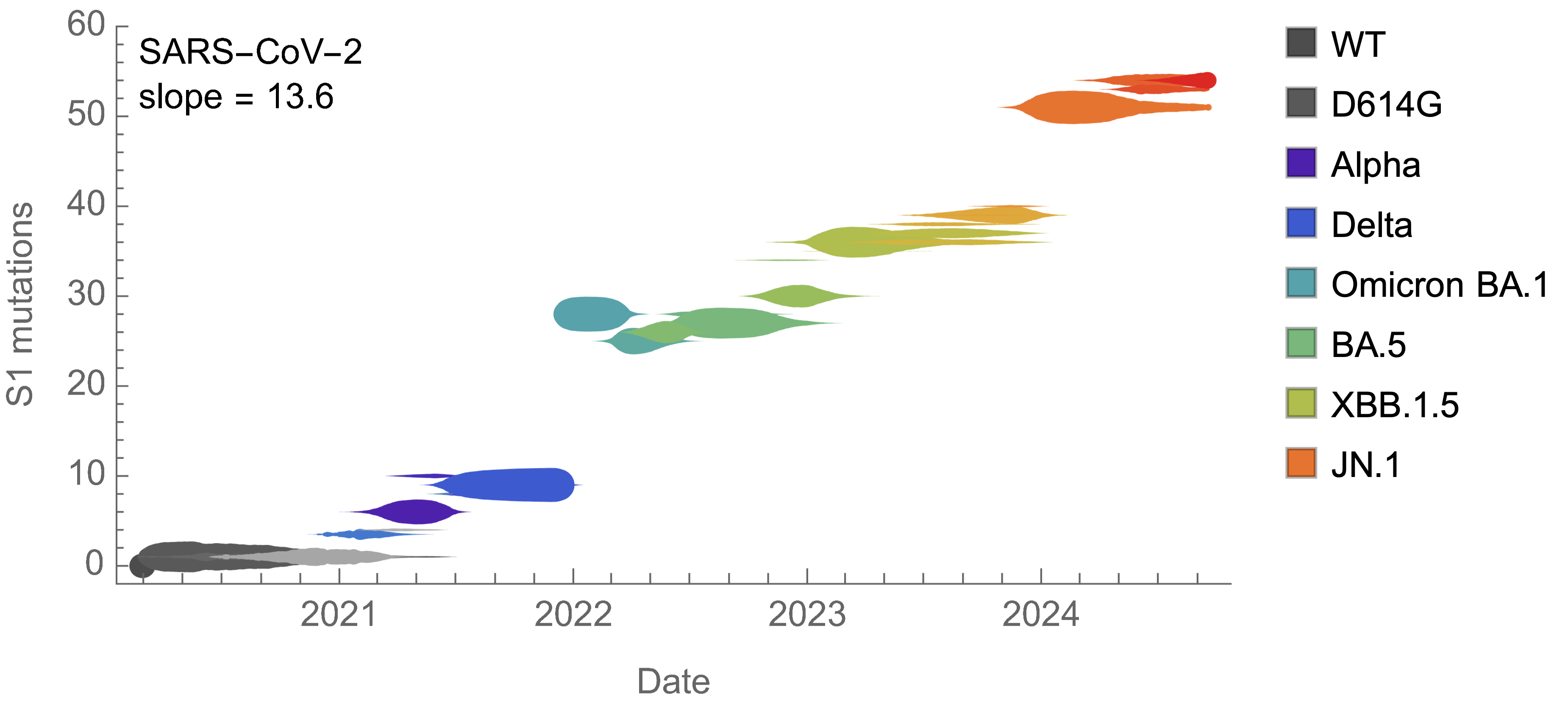
Consequently, we estimate that 14 mutations to spike S1 will result in a doubling of fitness
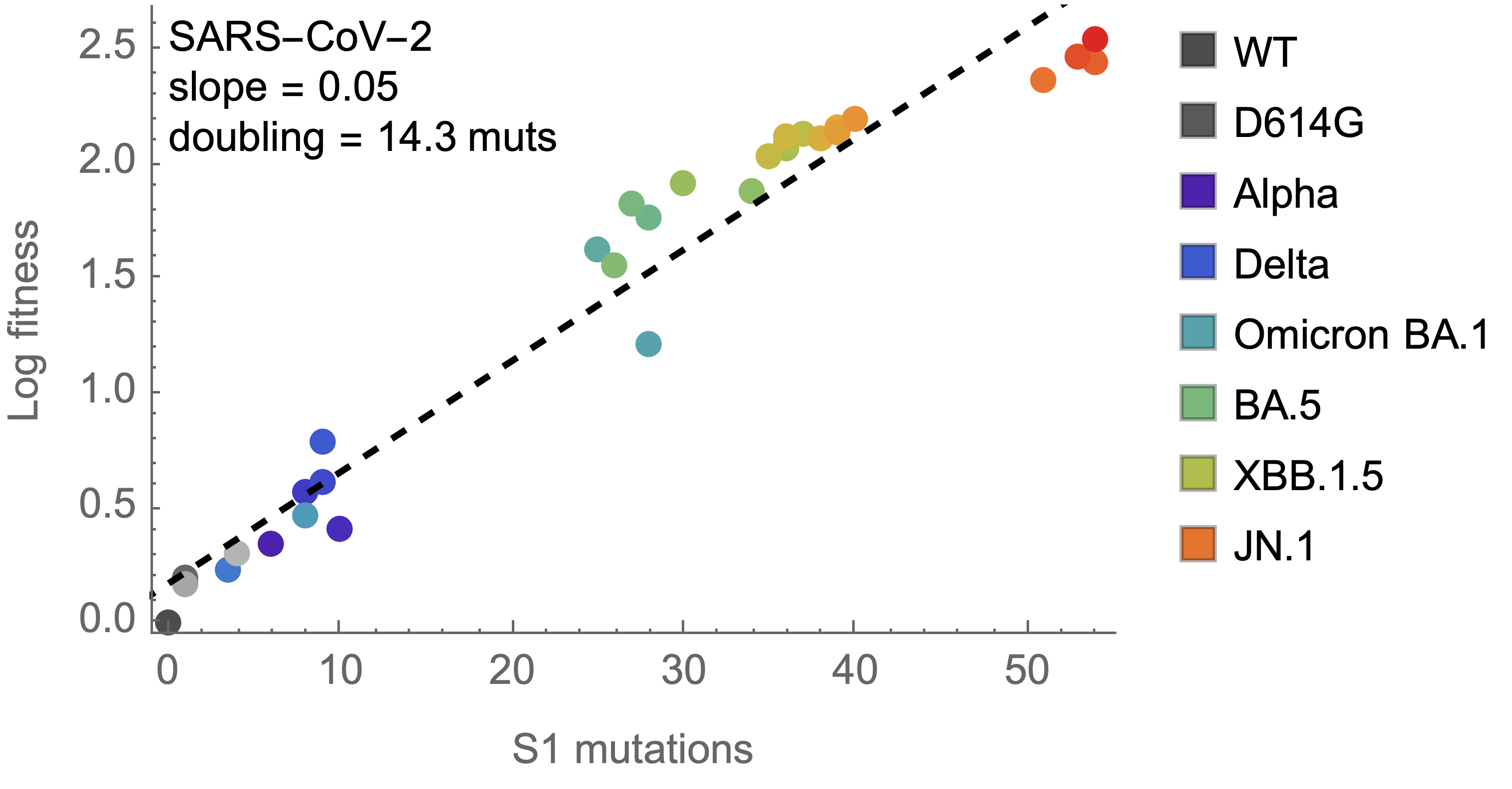
Differences with influenza H3N2 are perhaps instructive
Evolutionary forecasting
Assessing MLR models for short-term frequency forecasting
Retrospective projections twice monthly during 2022
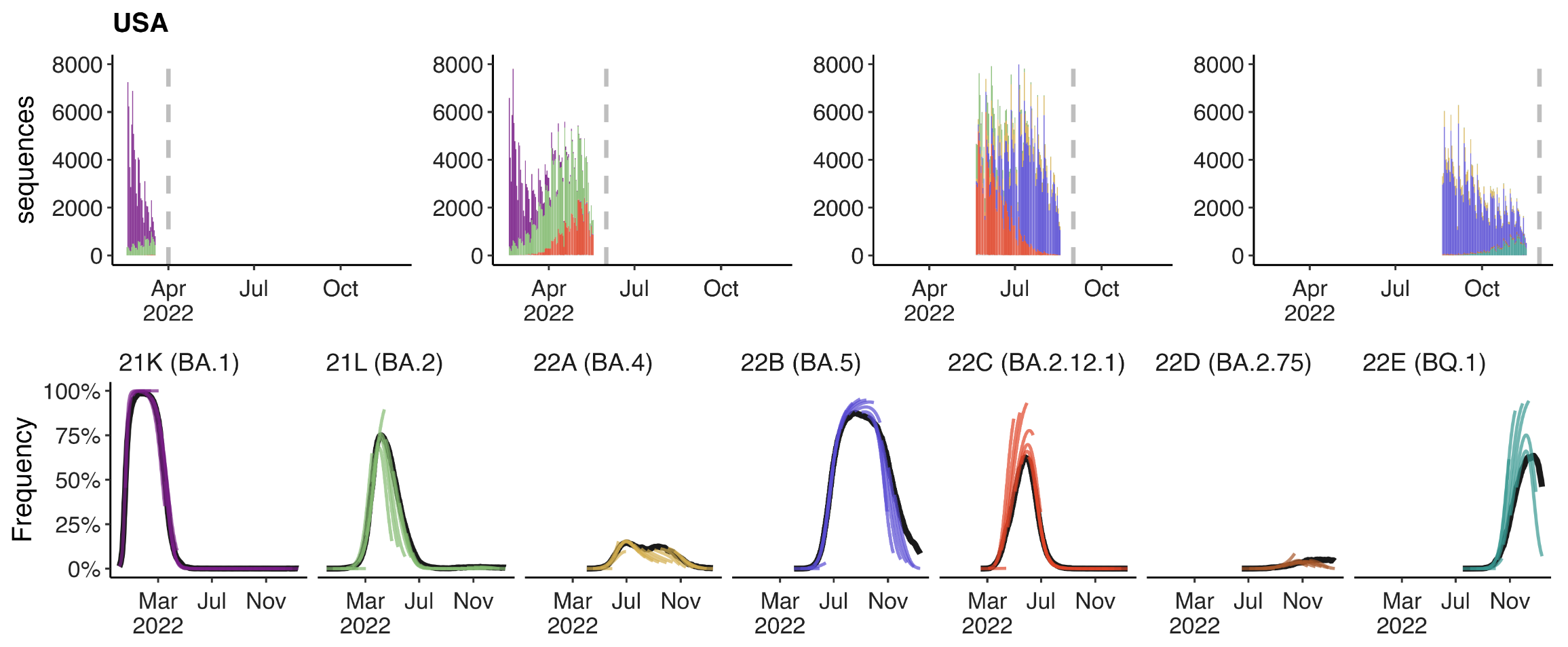
+30 day short-term forecasts across different countries
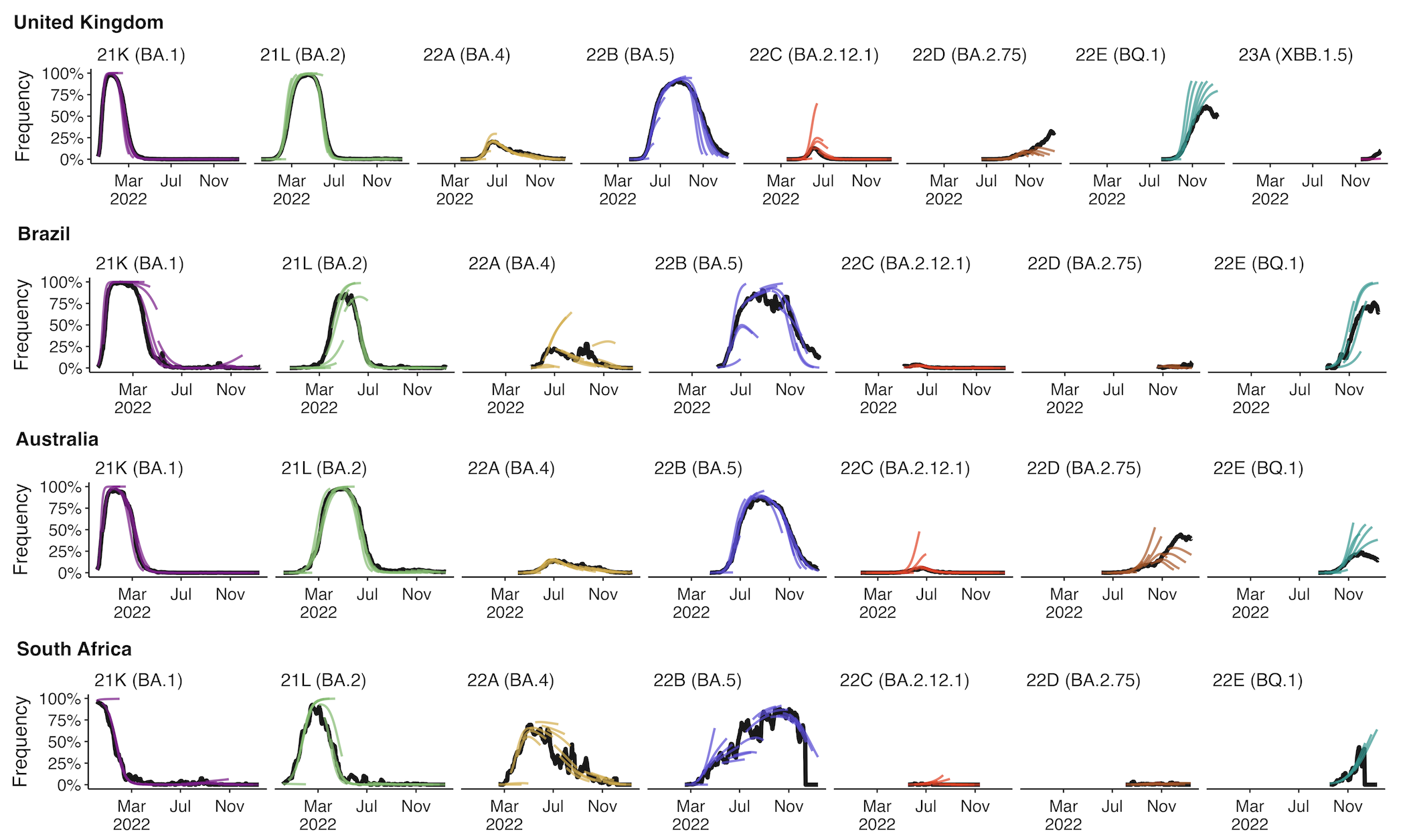
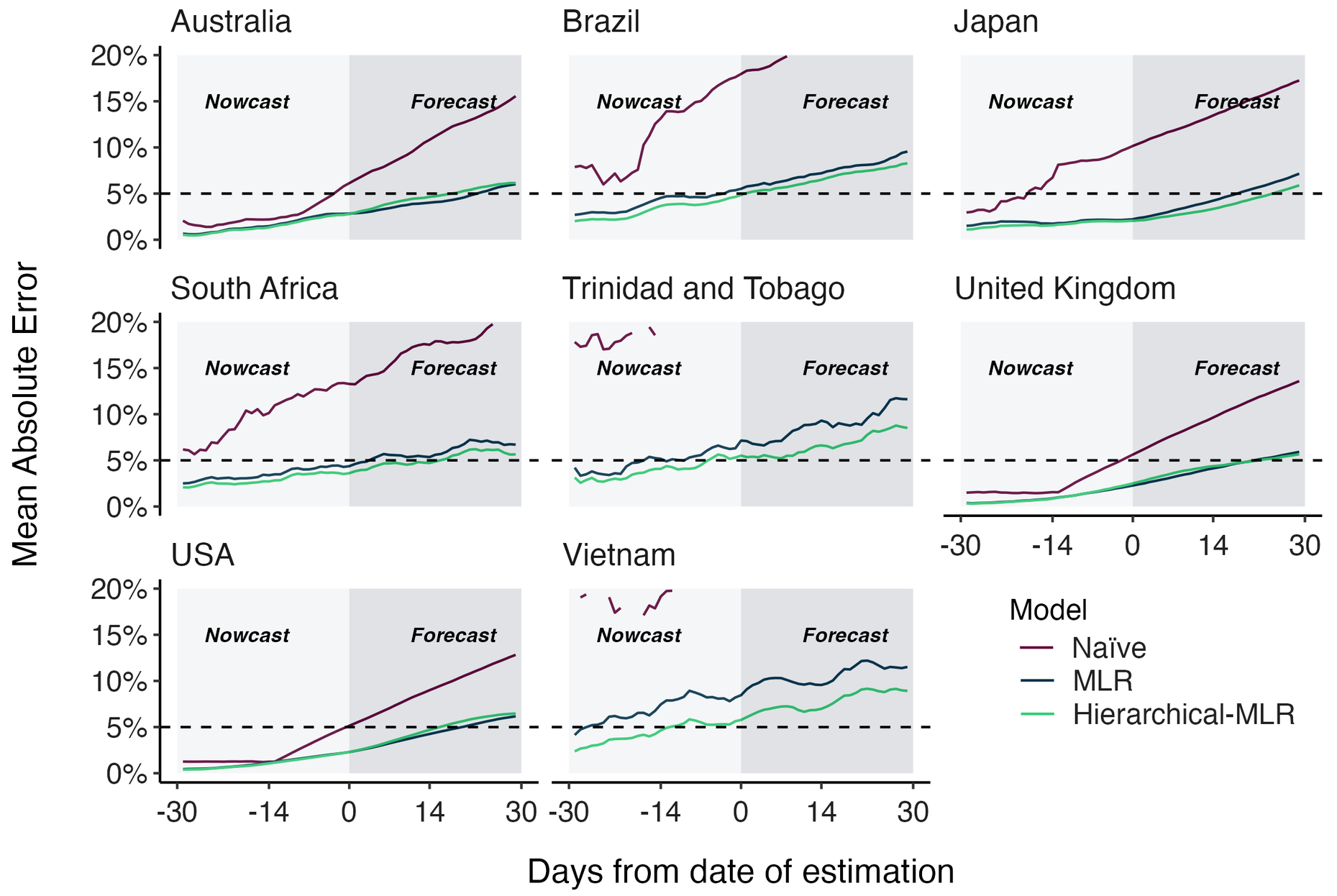
MLR models generate accurate short-term forecasts
30 days out, countries range from 5 to 15% mean absolute error
Correlates with data availability (median number of sequences available from the previous 30 days):
- USA
- ~45k sequences
- Australia
- ~4k sequences
- South Africa
- 170 sequences
- Vietnam
- 30 sequences
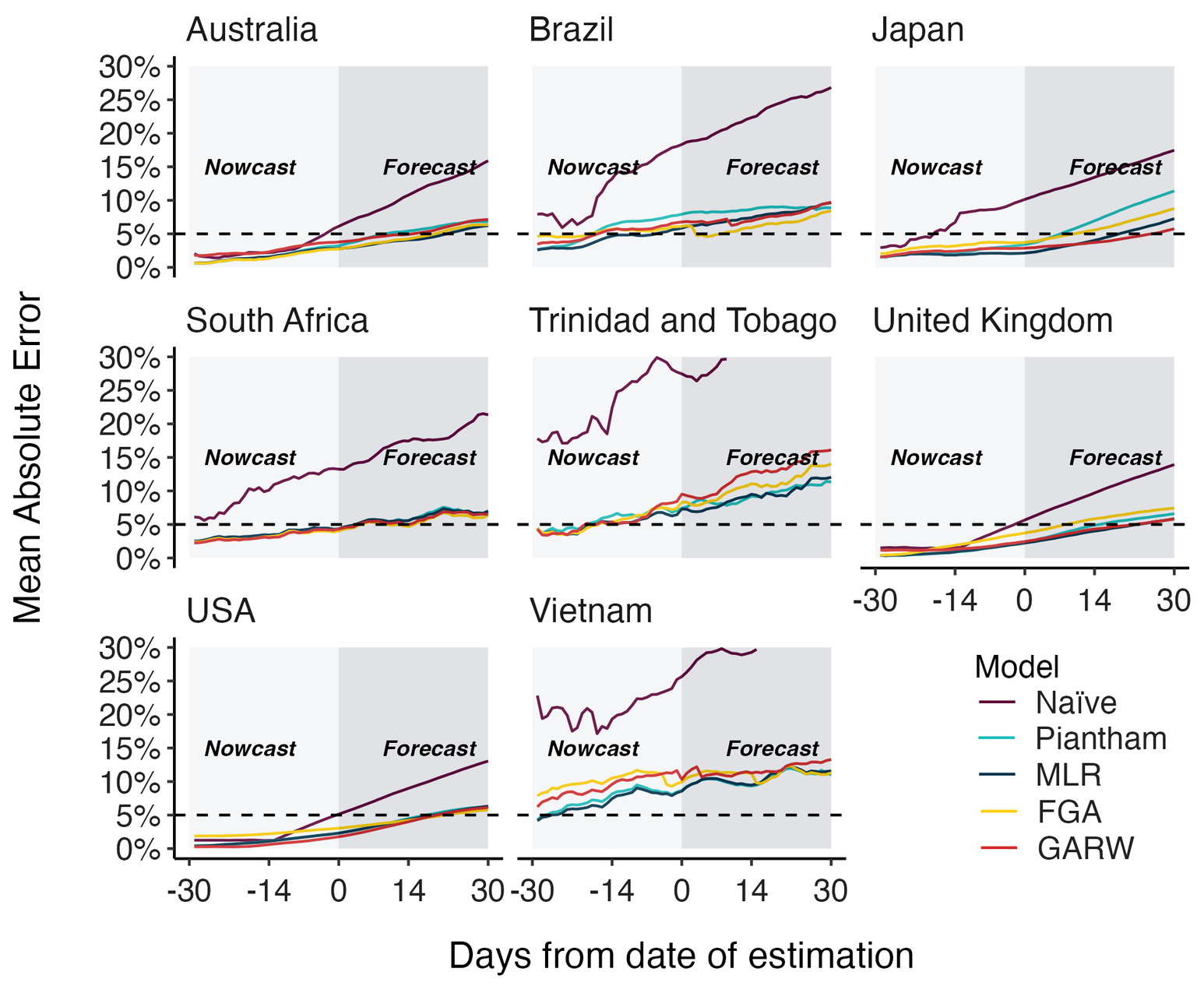
Hierarchical MLR model pools variant fitness estimates across countries
This approach improves poor model accuracy in countries with less intensive genomic surveillance
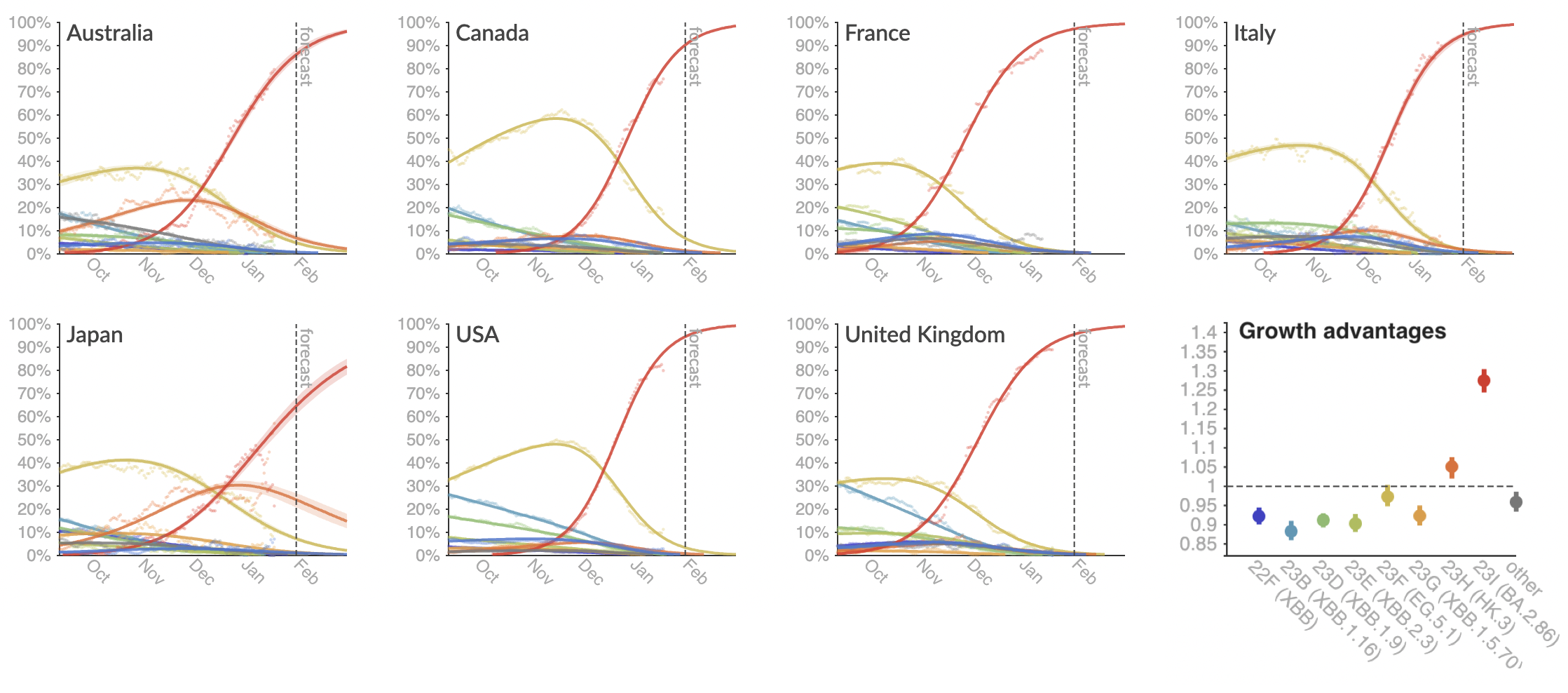
Clade and lineage forecasts continuously updated at nextstrain.org
Rapid sweep of JN.1 over Dec to Jan 2024
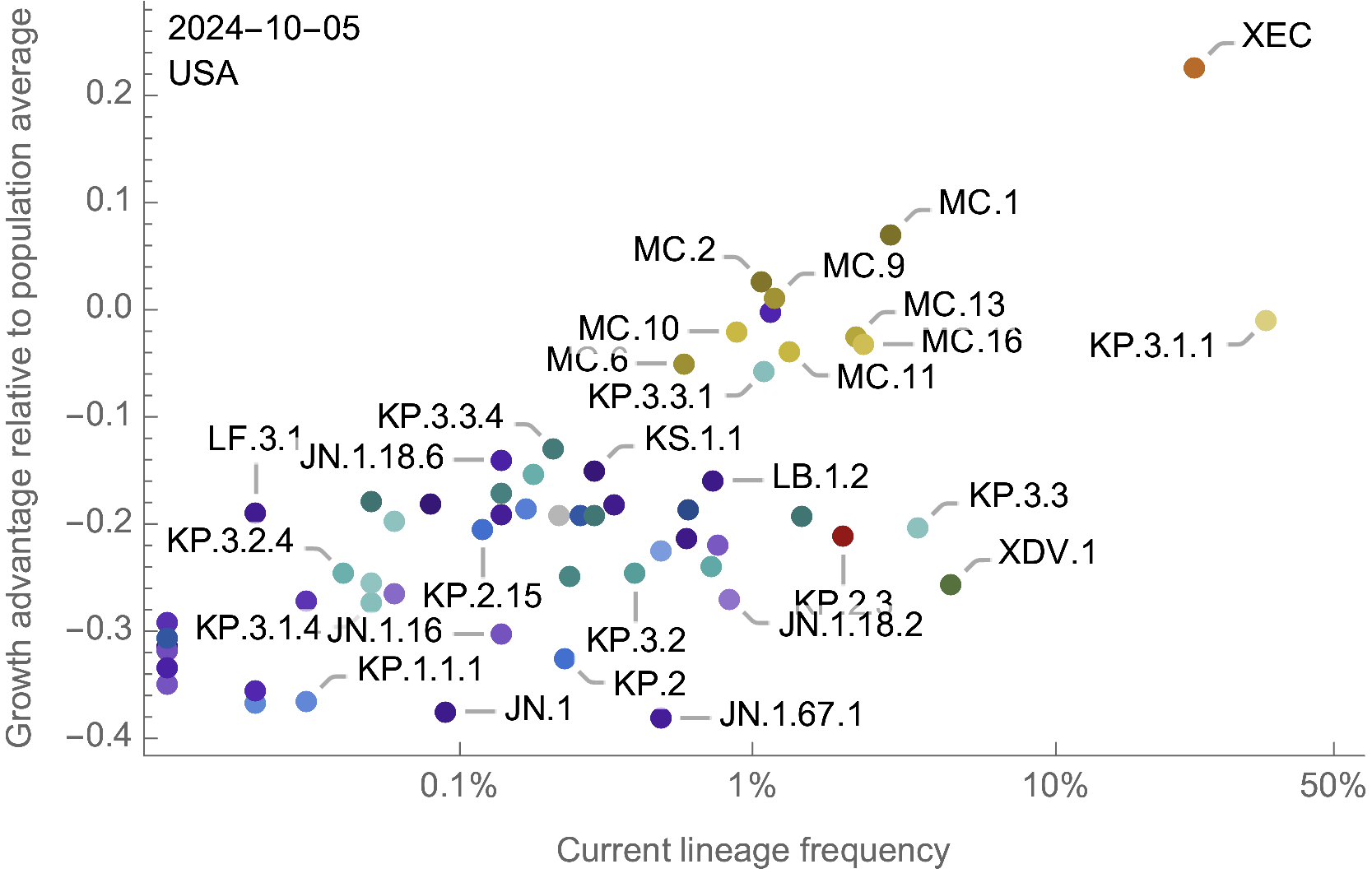
Assess currently circulating lineages by comparing frequency to population weighted growth advantage
Eventual lineage success largely determined by initial fitness
Eventual lineage success largely determined by initial fitness
Eventual lineage success largely determined by initial fitness
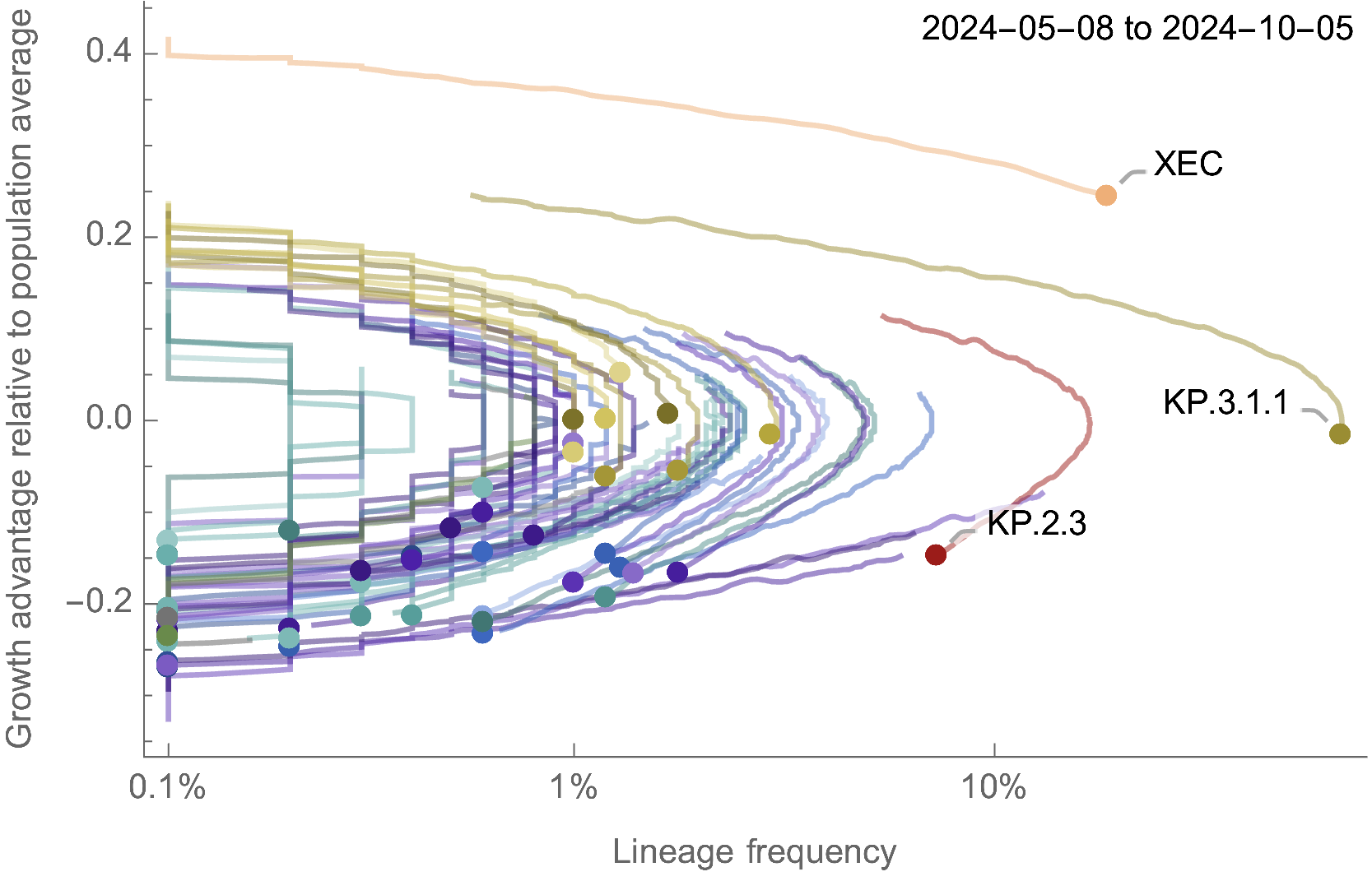
Picking the winner among circulating SARS-CoV-2 variants is a solved problem, but impactful mutations arise fast enough that the prediction horizon is limited to 2-3 months
Ongoing work to lengthen prediction horizon by incorporating high-throughput experimental measurements of ACE2 binding and immune escape
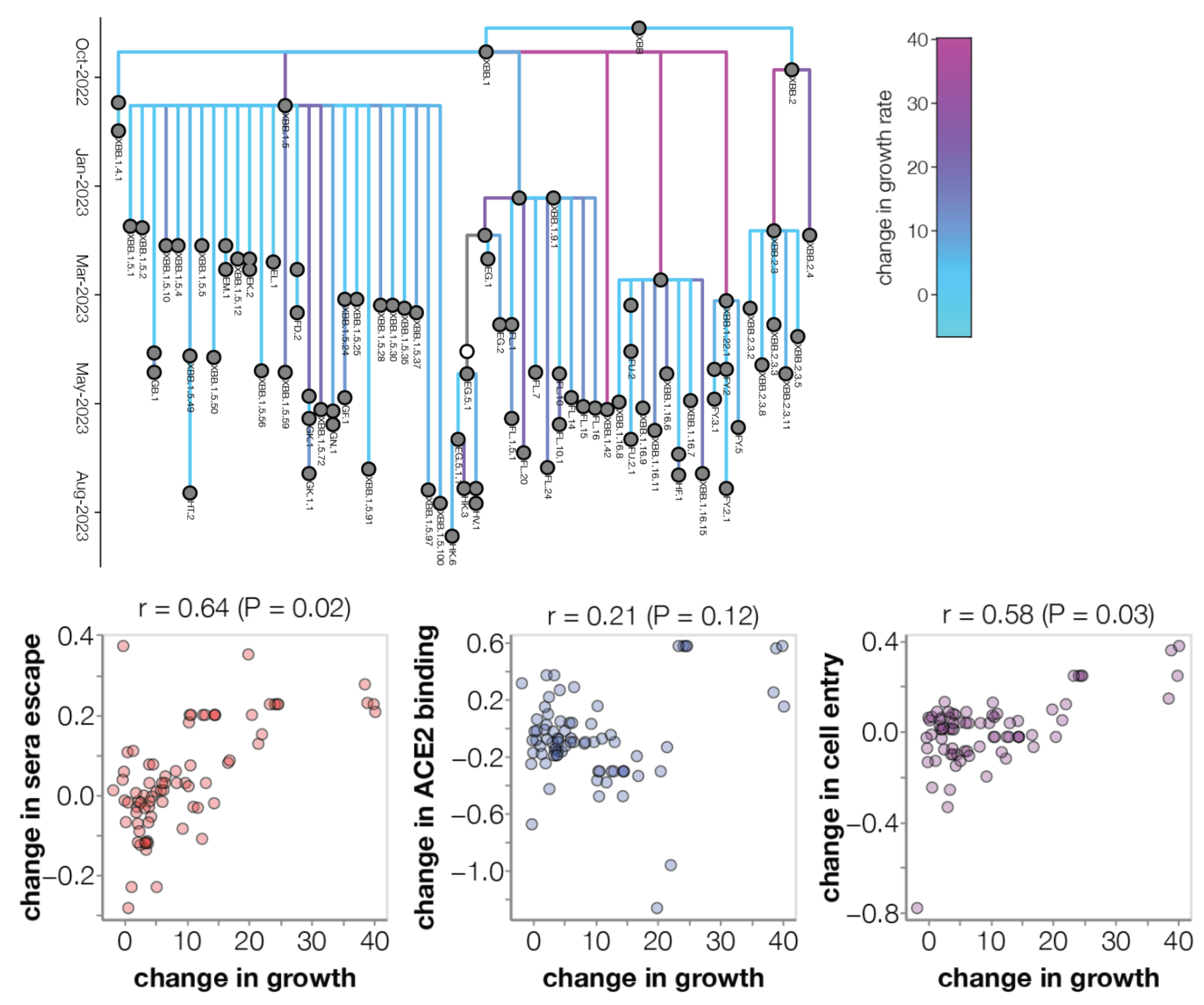
Prediction of variant fitness from empirical priors
Rather than estimate variant specific fitness $f_i$ directly, we instead parameterize as the "innovation" in fitness in going from parent lineage $p$ to child lineage $i$ as $\psi_i = (f_i - f_p)$.
We then compare a non-informative model of $$\psi_i = (f_i - f_p) \sim \mathrm{Normal}(0, \sigma)$$ to a model where each "innovation" value has an informed prior based on a linear combination of predictors such as ACE2 binding, immune escape and S1 mutations, where $z_k$ represents the value of predictor $k$ $$\psi_i = (f_i - f_p) \sim \mathrm{Normal}\left(\sum_k \beta_k \, z_k, \sigma\right)$$
Figgins et al. In prep.
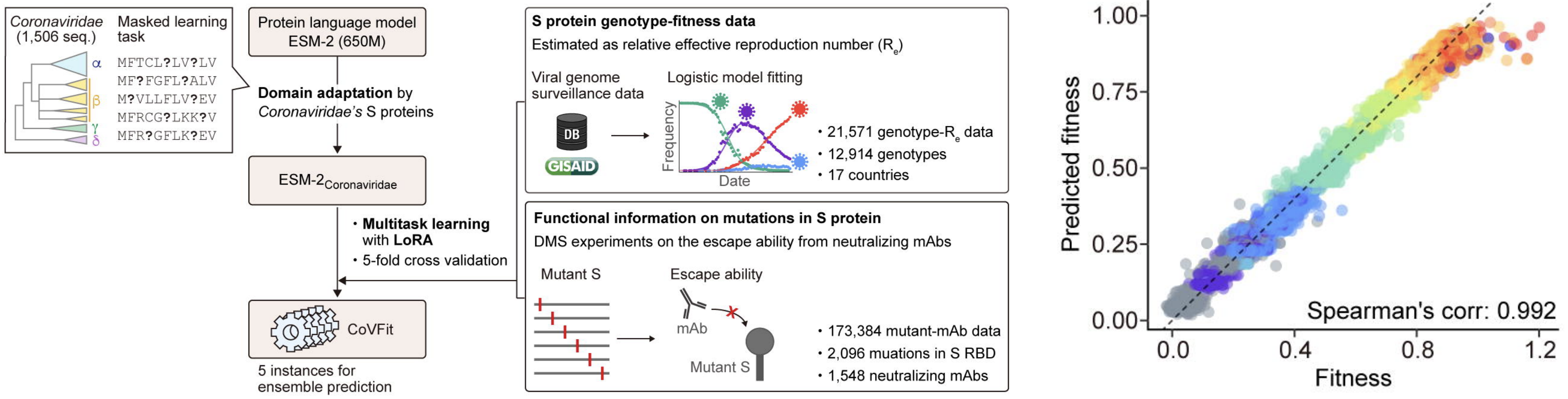
Exciting developments in applying protein language models to estimate sequence-level fitness
It's tough to make predictions,
especially out of sample
Acknowledgements
SARS-CoV-2 genomic epi: Data producers from all over the world, GISAID
Nextstrain: Richard Neher, Ivan Aksamentov, John SJ Anderson, Kim Andrews, Jennifer Chang, James Hadfield, Emma Hodcroft, John Huddleston, Jover Lee, Victor Lin, Cornelius Roemer, Thomas Sibley
Adaptive evolution across human endemic viruses: Katie Kistler
MLR and evolutionary forecasting: Marlin Figgins, Eslam Abousamra, Jover Lee, James Hadfield, John Huddleston, Jesse Bloom, Cornelius Roemer, Richard Neher
Bedford Lab:
John Huddleston,
James Hadfield,
Katie Kistler,
Thomas Sibley,
Jover Lee,
Miguel Paredes,
Marlin Figgins,
Victor Lin,
Jennifer Chang,
Nashwa Ahmed,
Cécile Tran Kiem,
Kim Andrews,
Cristian Ovaduic,
Philippa Steinberg,
Jacob Dodds,
John SJ Anderson
Amin Bemanian
