Fitness flux in SARS-CoV-2 and seasonal influenza H3N2
Trevor Bedford
Fred Hutchinson Cancer Center / Howard Hughes Medical Institute
3 Mar 2025
CEPR Seminar
London School of Hygiene and Tropical Medicine
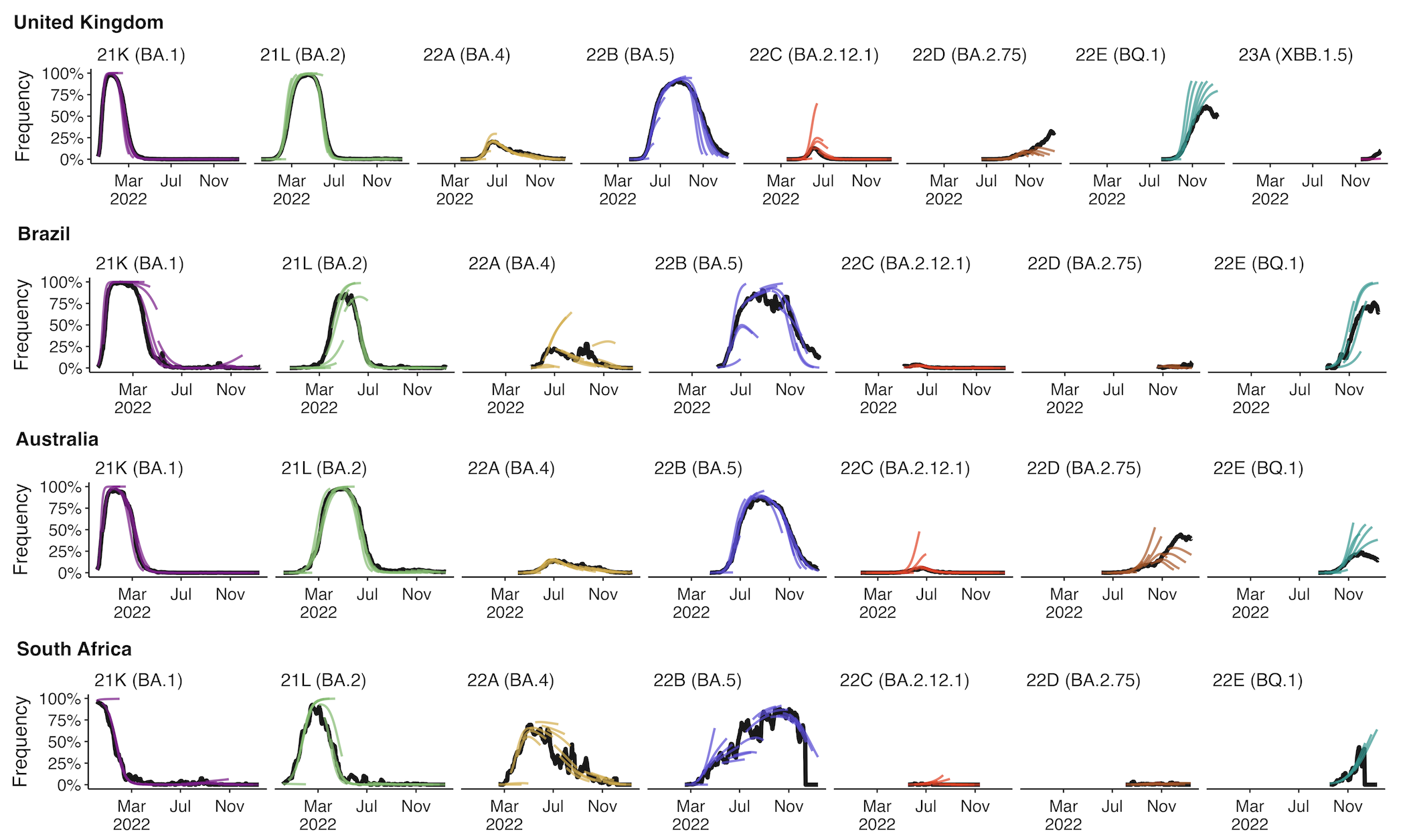
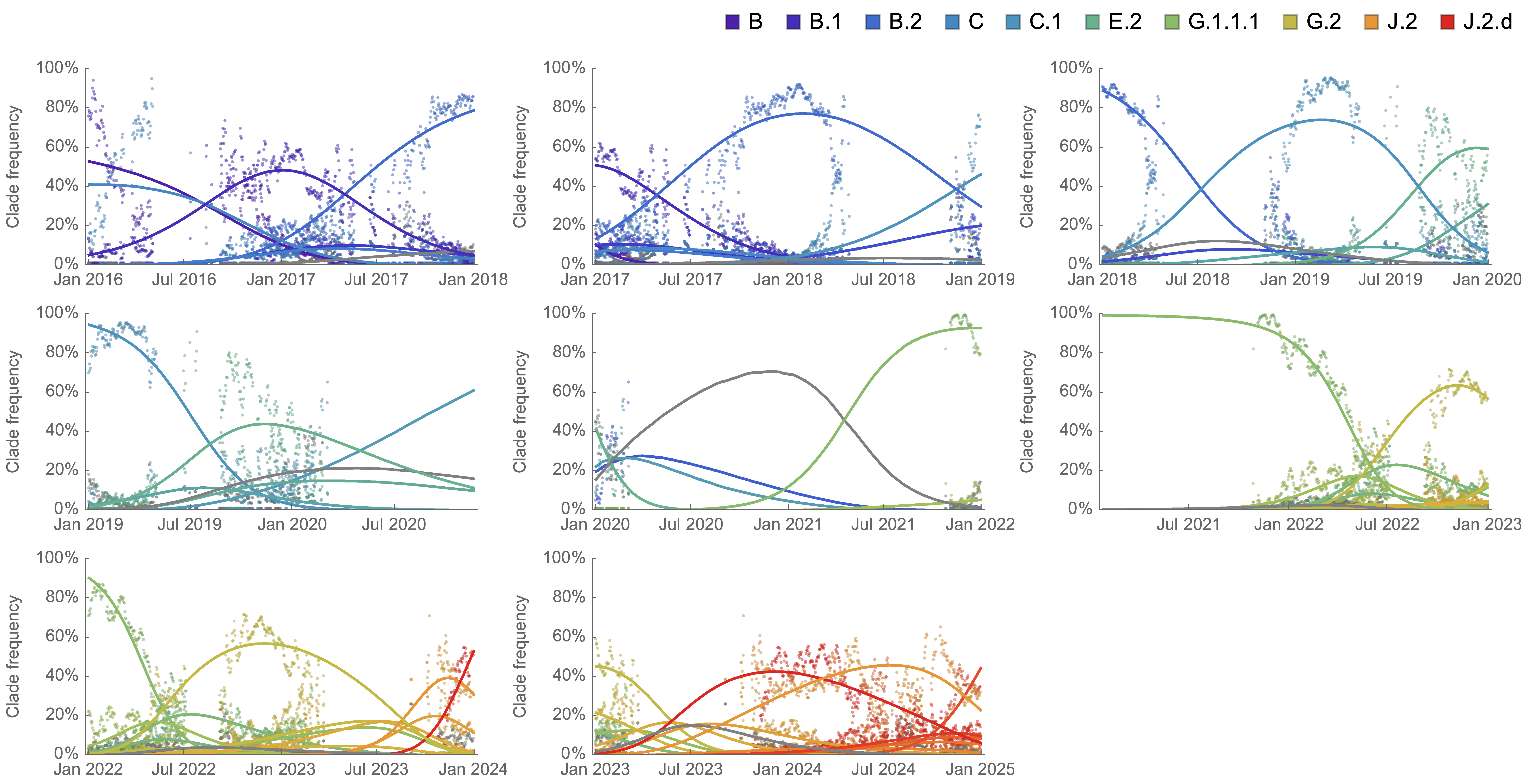
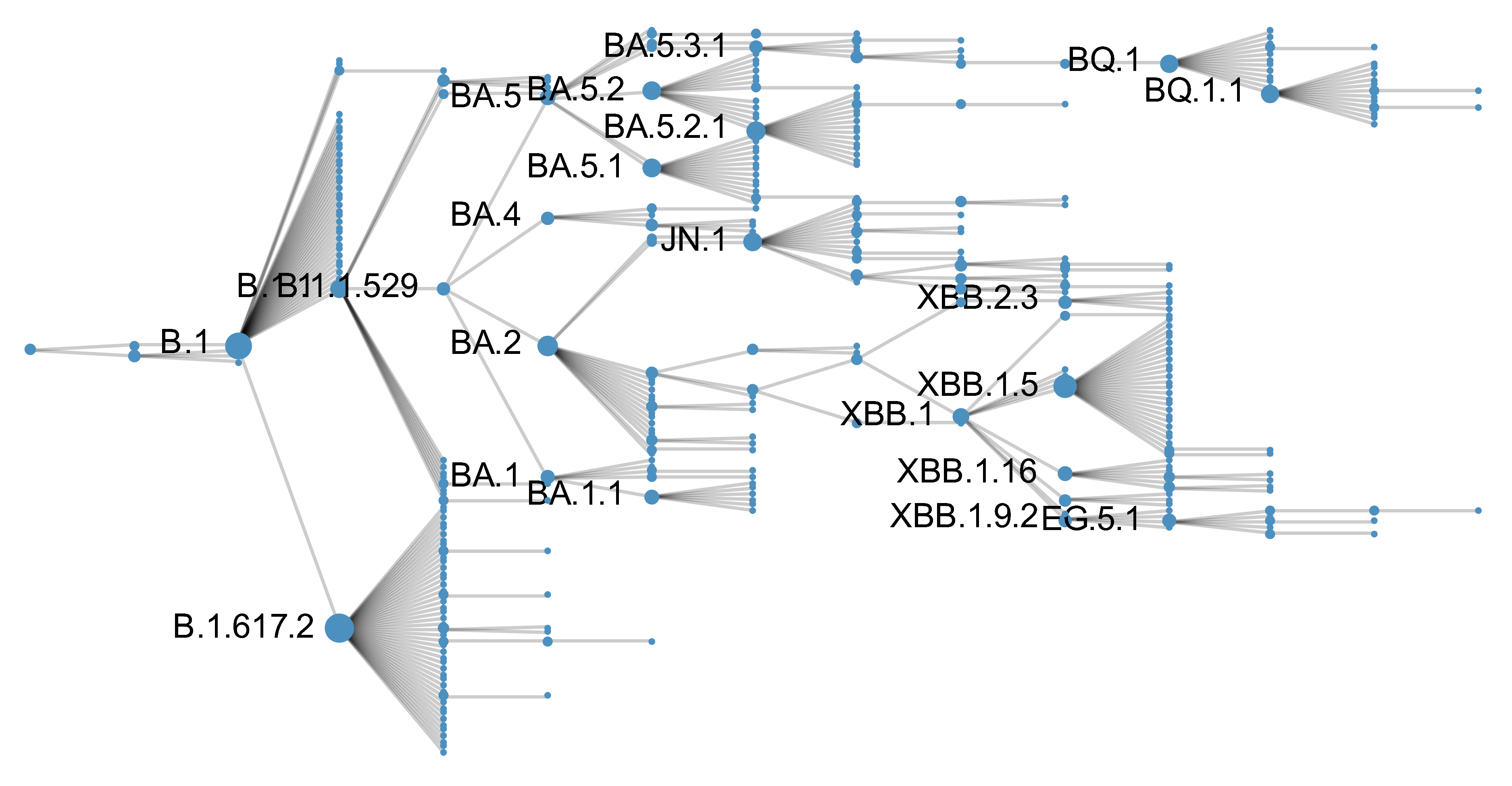
Genetic relationships of globally sampled SARS-CoV-2 from 2020 to present
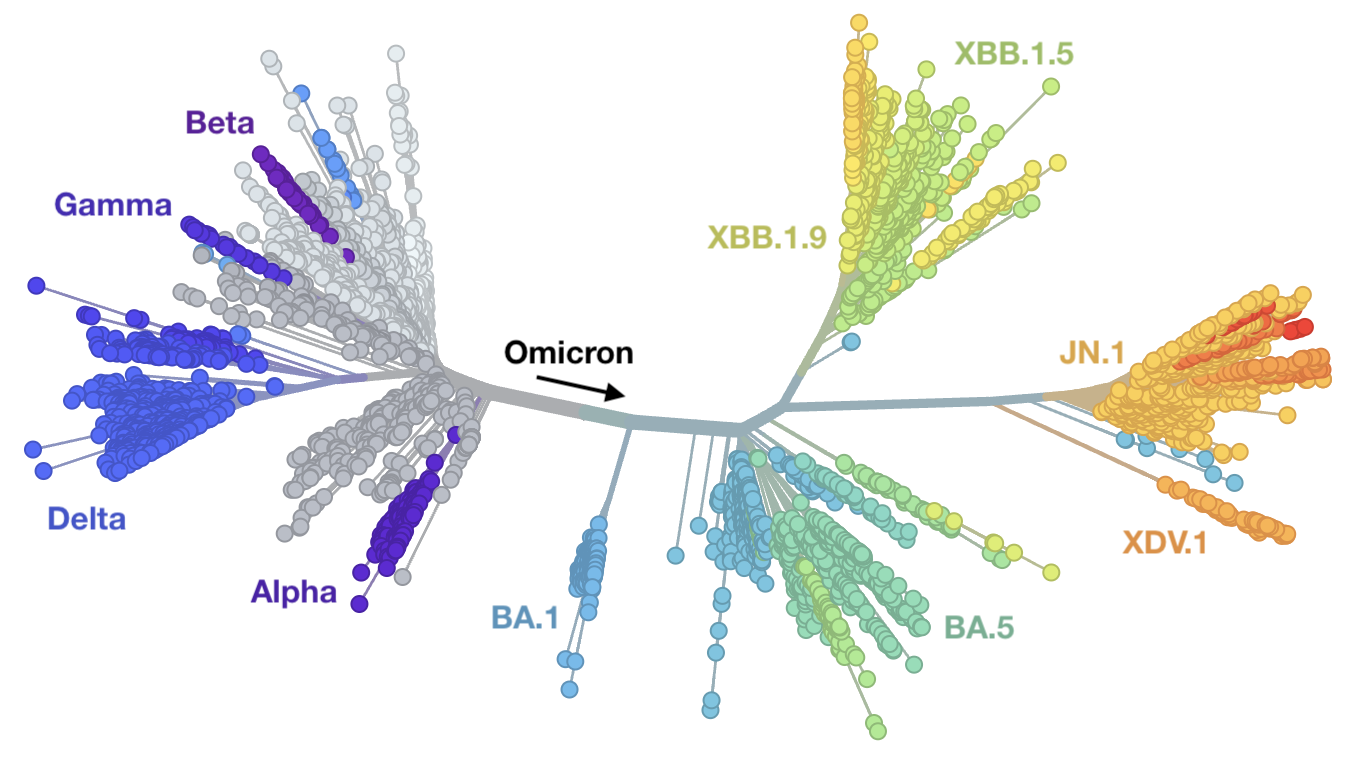
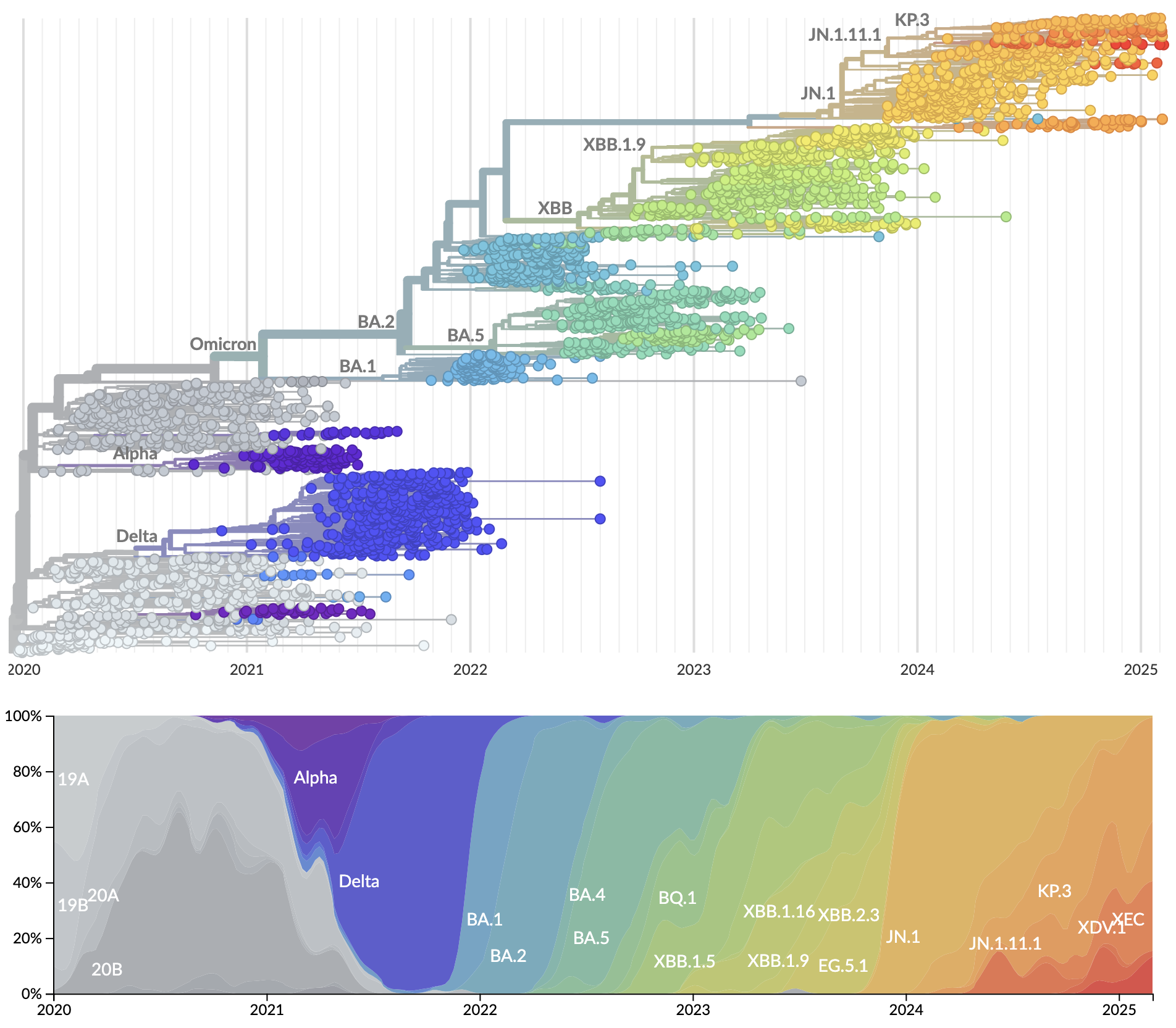
Rapid displacement of existing diversity by emerging variants
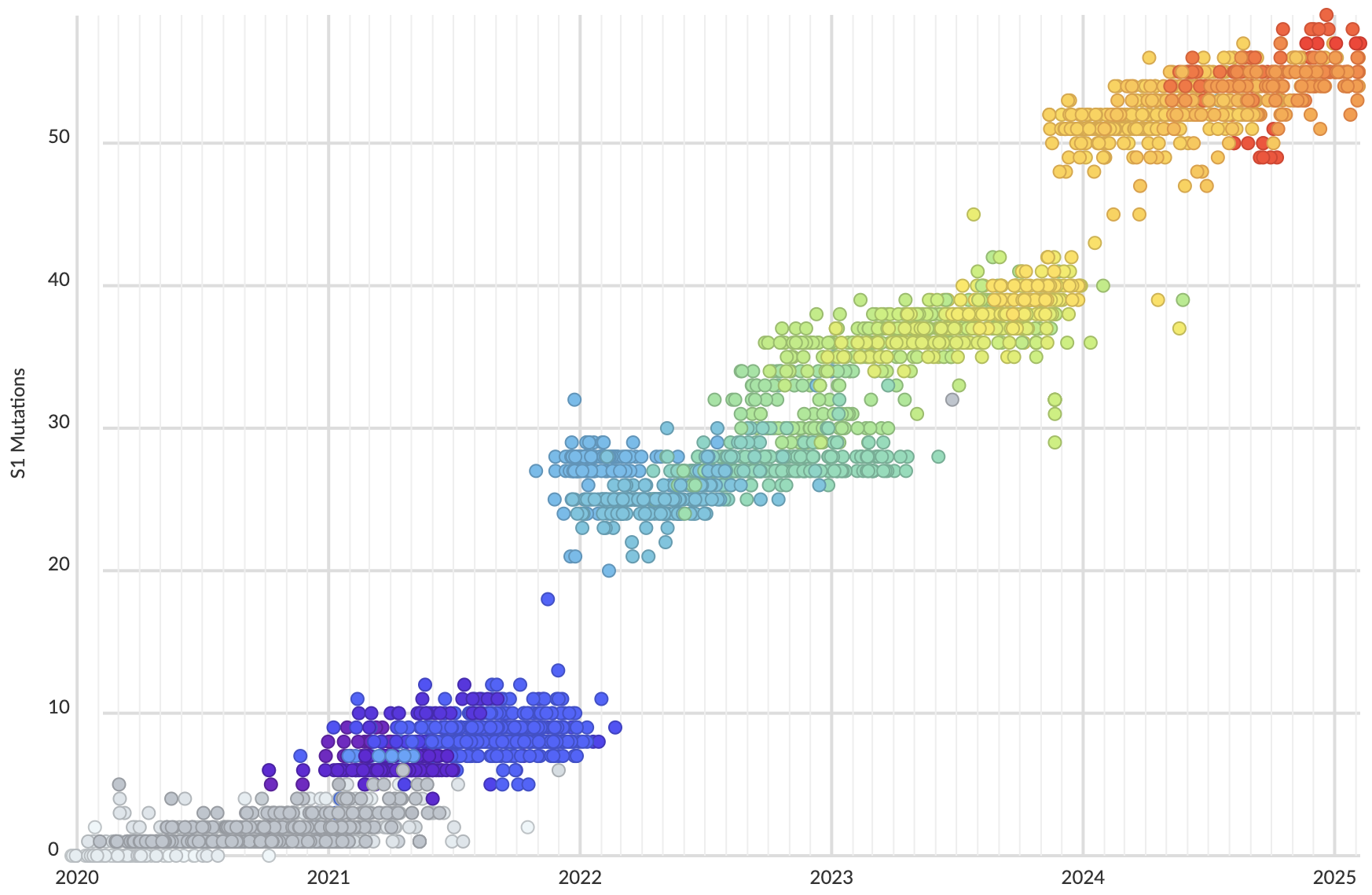
Mutations in S1 domain of spike protein driving displacement
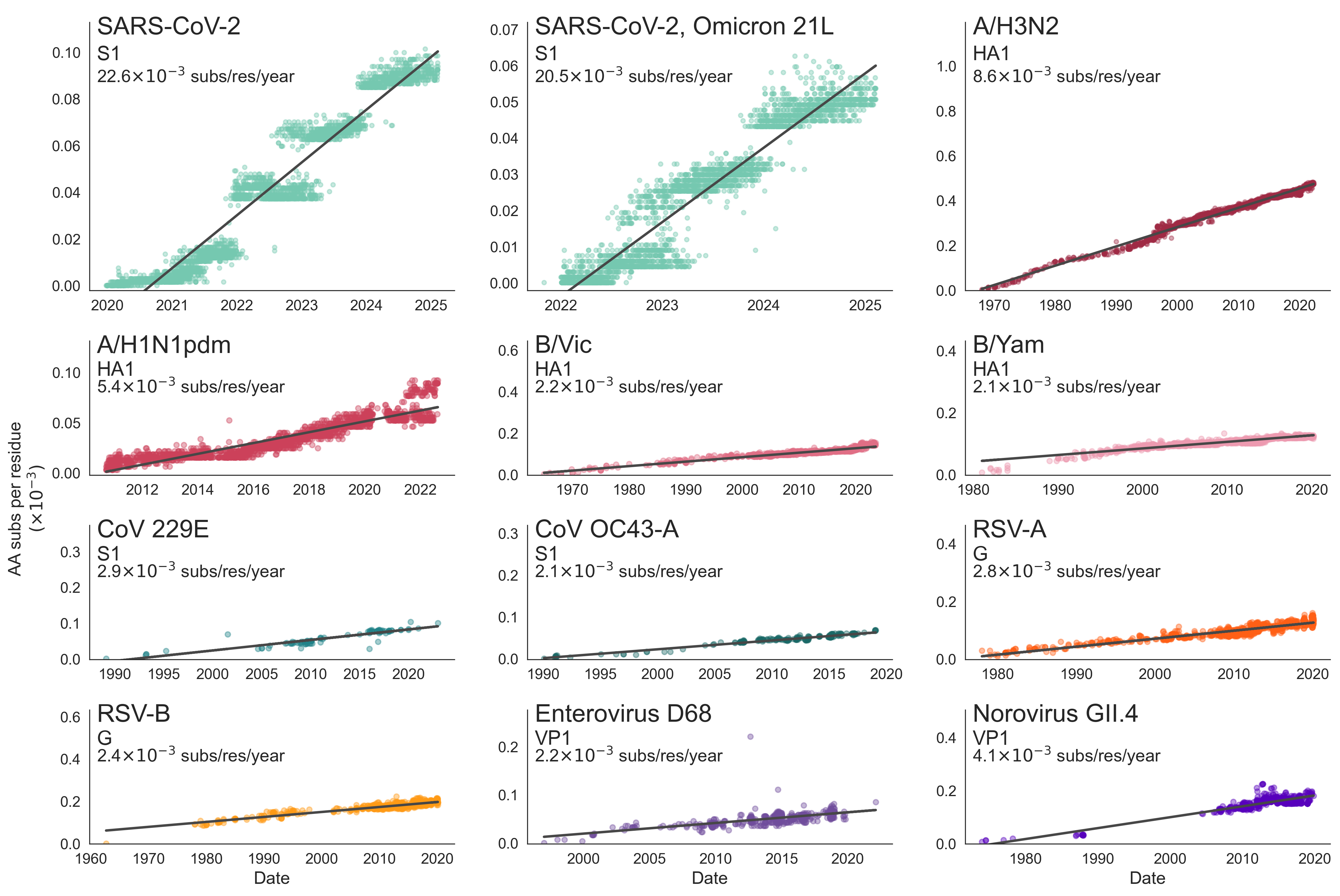
SARS-CoV-2 evolution fast relative to previous endemic viruses
Method from Kistler and Bedford. 2023. Cell Host Microbe.
This talk
- Frequency dynamics and fitness estimation
- Evolutionary forecasting
- Fitness flux
- Mutational fitness effects
Frequency dynamics and fitness estimation
Population genetic expectation of variant frequency under selection
$x' = \frac{x \, (1+s)}{x \, (1+s) + (1-x)}$ for frequency $x$ over one generation with selective advantage $s$
$x(t) = \frac{x_0 \, (1+s)^t}{x_0 \, (1+s)^t + (1-x_0)}$ for initial frequency $x_0$ over $t$ generations
Trajectories are linear once logit transformed via $\mathrm{log}(\frac{x}{1 - x})$
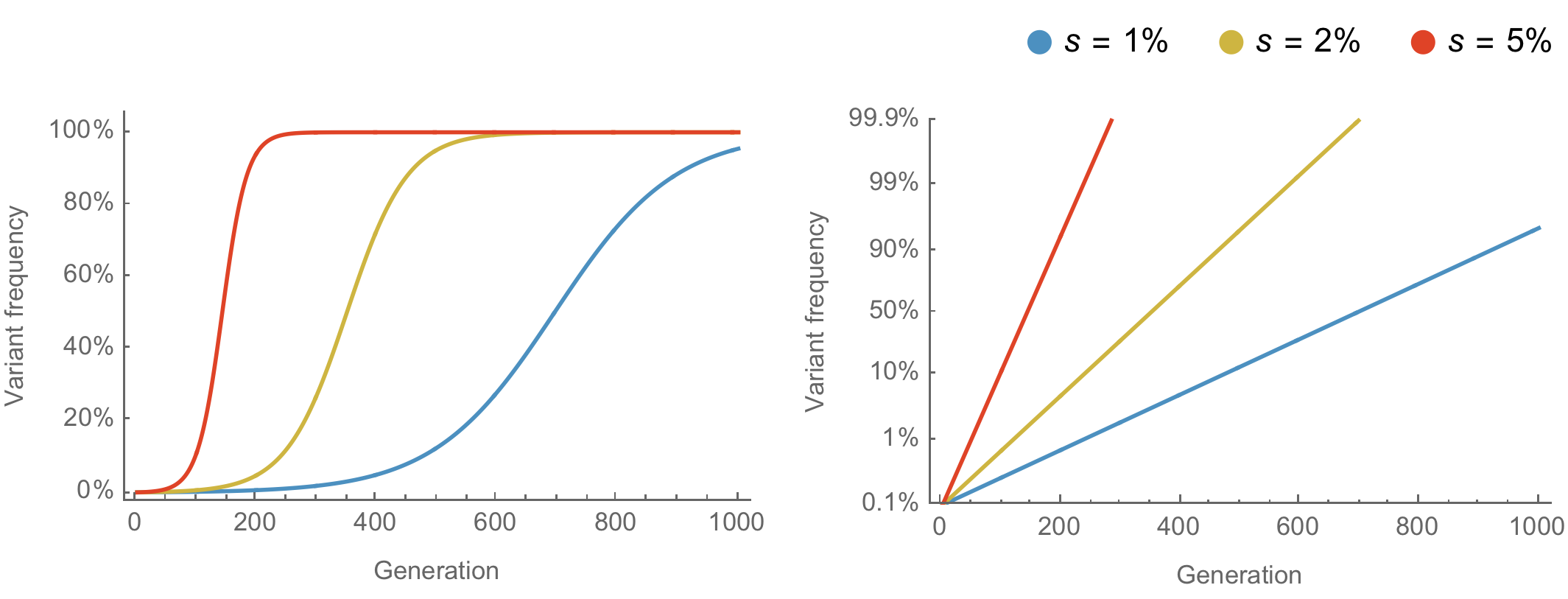
Consistent frequency dynamics in logit space (BA.2 Mar 2022)
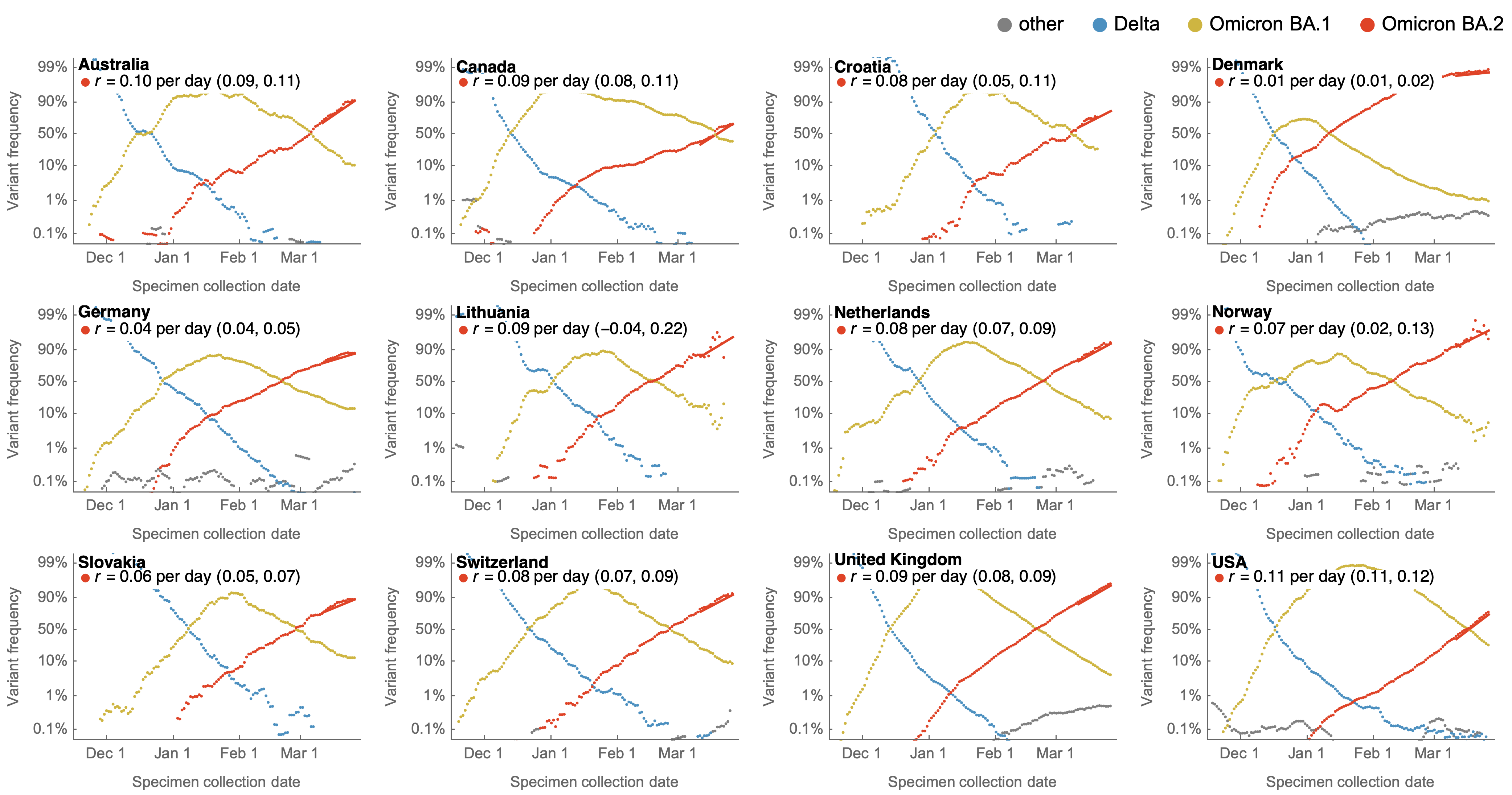
Consistent frequency dynamics in logit space (JN.1 Dec 2023)
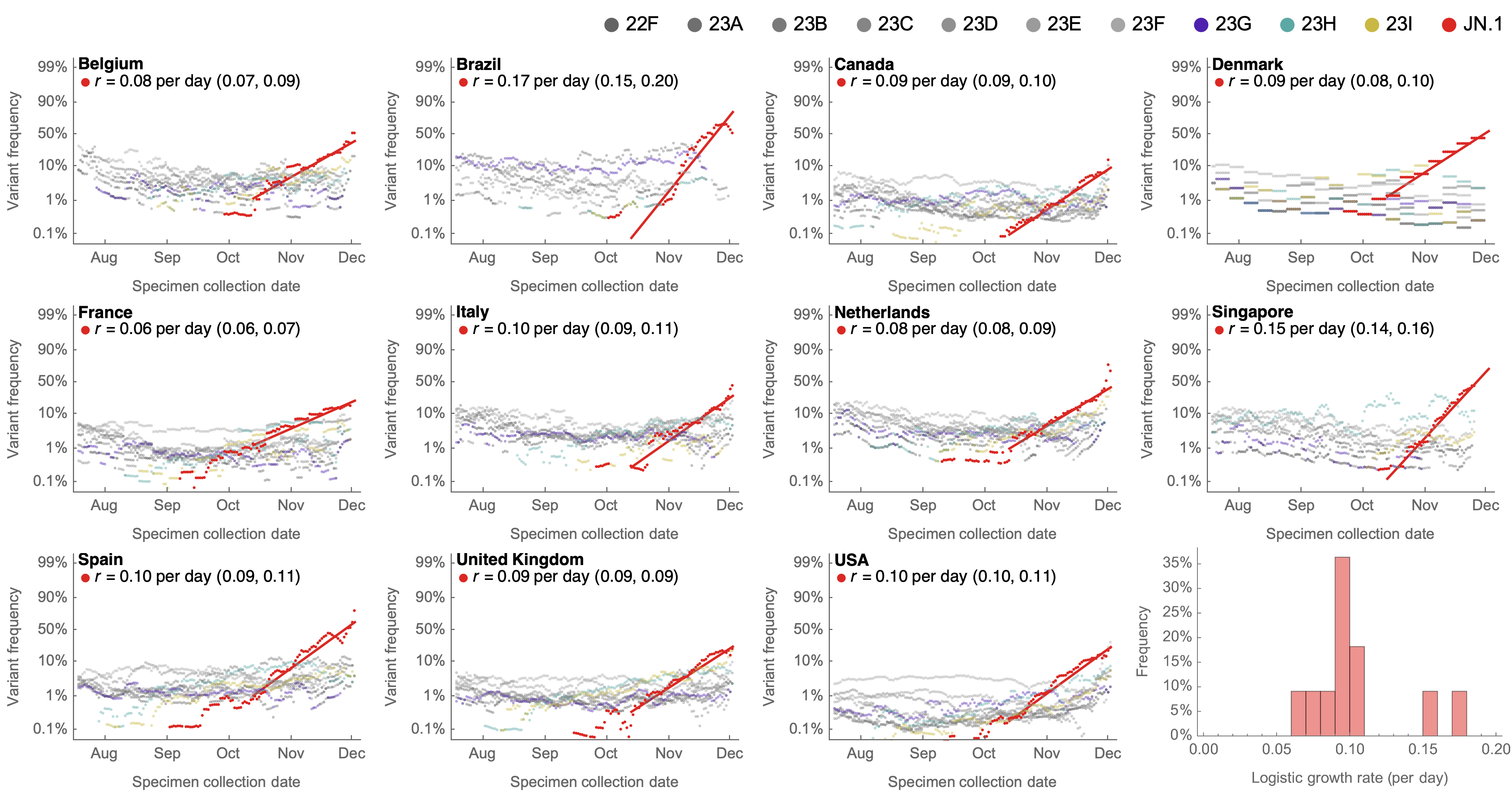
Multinomial logistic regression
Multinomial logistic regression across $n$ variants models the probability of a virus sampled at time $t$ belonging to variant $i$ as
$$\mathrm{Pr}(X = i) = x_i(t) = \frac{p_i \, \mathrm{exp}(f_i \, t)}{\sum_j p_j \, \mathrm{exp}(f_j \, t) }$$
with $2n$ parameters consisting of $p_i$ the frequency of variant $i$ at initial timepoint and $f_i$ the growth rate or fitness of variant $i$.
Various flavors of MLR implemented in evofr package
location variant date sequences Japan 22B 2023-02-10 242 Japan 22B 2023-02-11 56 Japan 22B 2023-02-12 70 Japan 22E 2023-02-10 80 Japan 22E 2023-02-11 21 Japan 22E 2023-02-12 27 USA 22B 2023-02-10 41 USA 22B 2023-02-11 23 USA 22B 2023-02-12 23 USA 22E 2023-02-10 368 USA 22E 2023-02-11 236 USA 22E 2023-02-12 246 ...
Multinomial logistic regression fits variant frequencies well
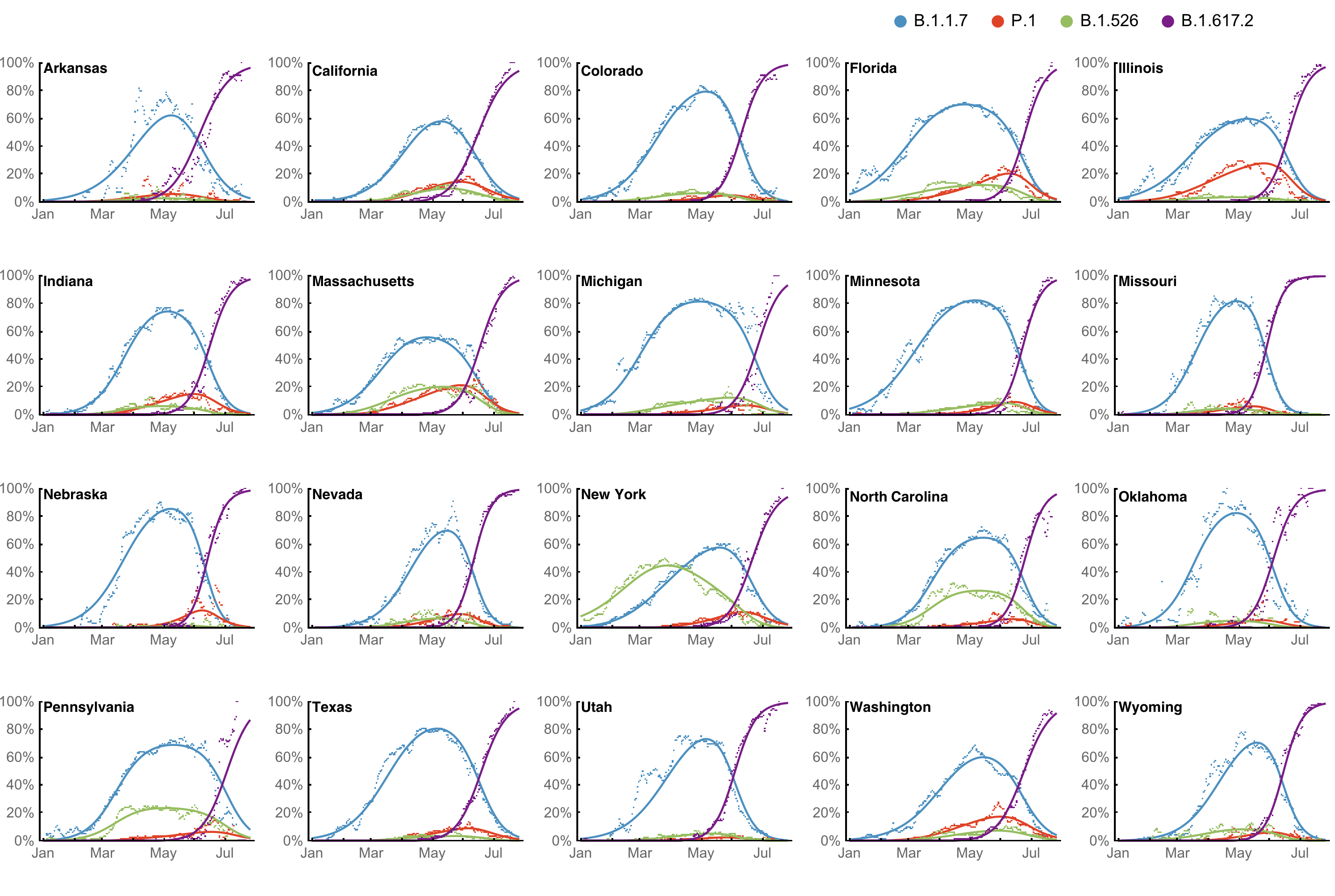
Original VOC viruses had substantially increased transmissibility
Model from Figgins and Bedford. 2022. medRxiv.
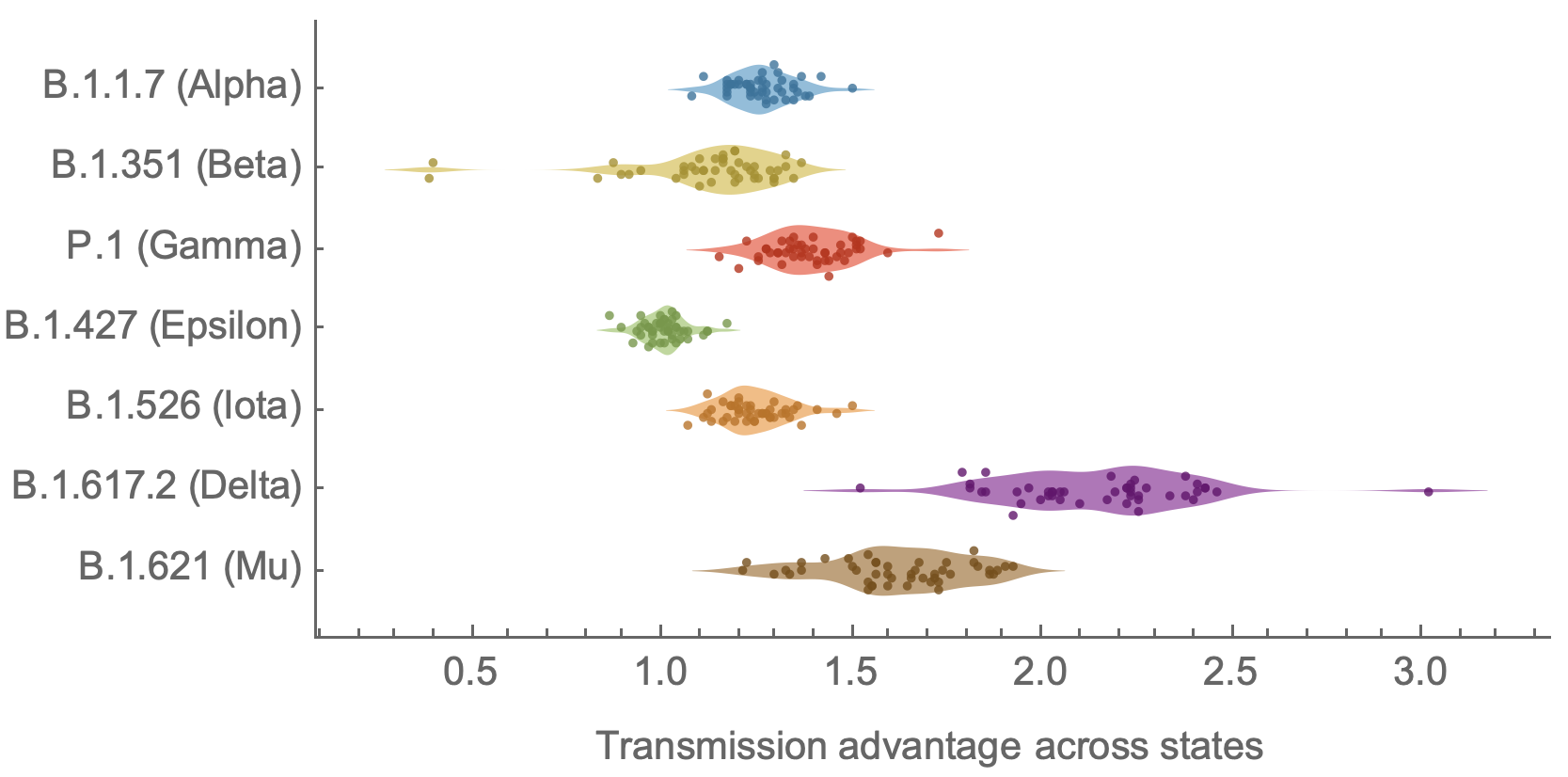
Evolutionary forecasting
Clade and lineage forecasts continuously updated at nextstrain.org
Rapid sweep of JN.1 over Dec to Jan 2024
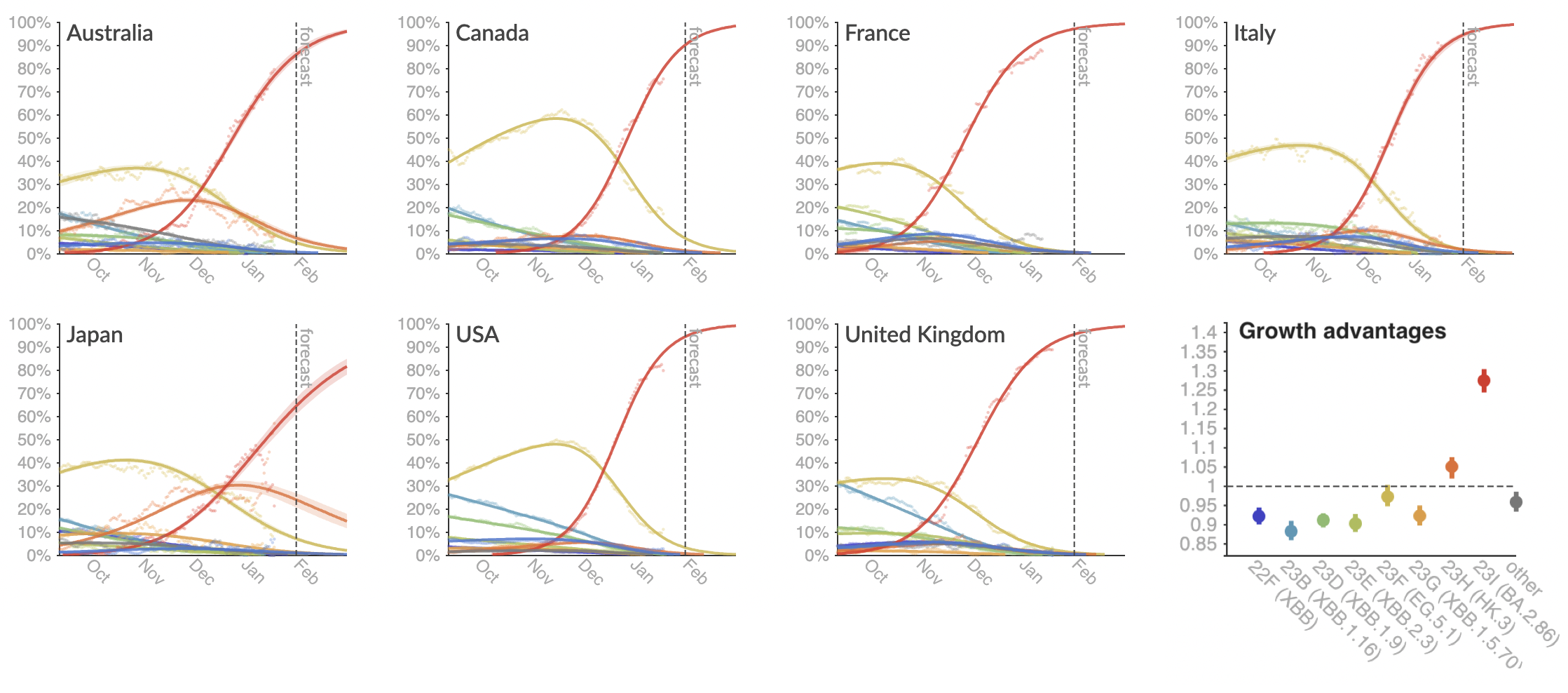
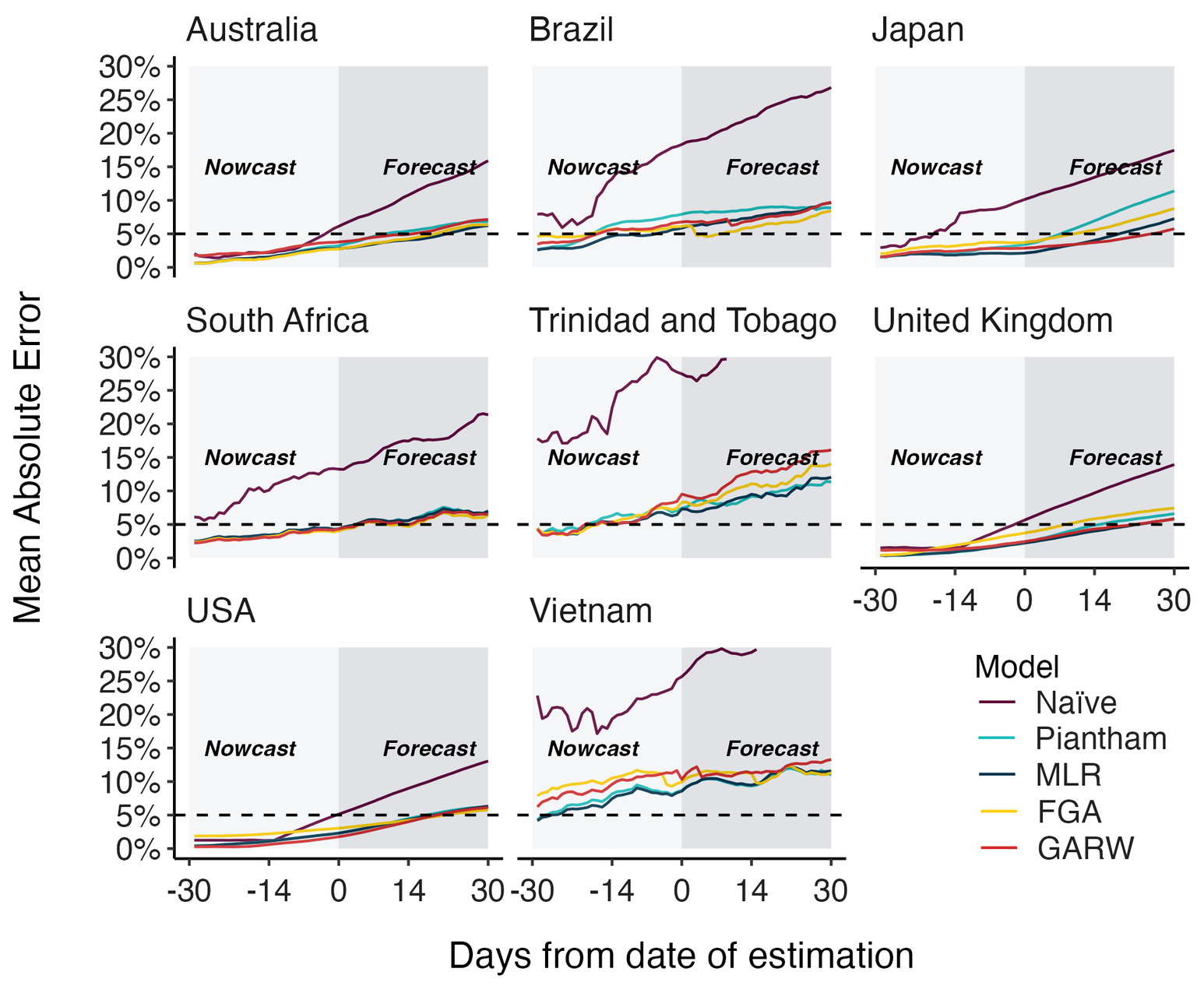
Assessing MLR models for short-term frequency forecasting
Retrospective projections twice monthly during 2022
+30 day short-term forecasts across different countries
MLR models generate accurate short-term forecasts
30 days out, countries range from 5 to 15% mean absolute error
Correlates with data availability (median number of sequences available from the previous 30 days):
- USA
- ~45k sequences
- Australia
- ~4k sequences
- South Africa
- 170 sequences
- Vietnam
- 30 sequences
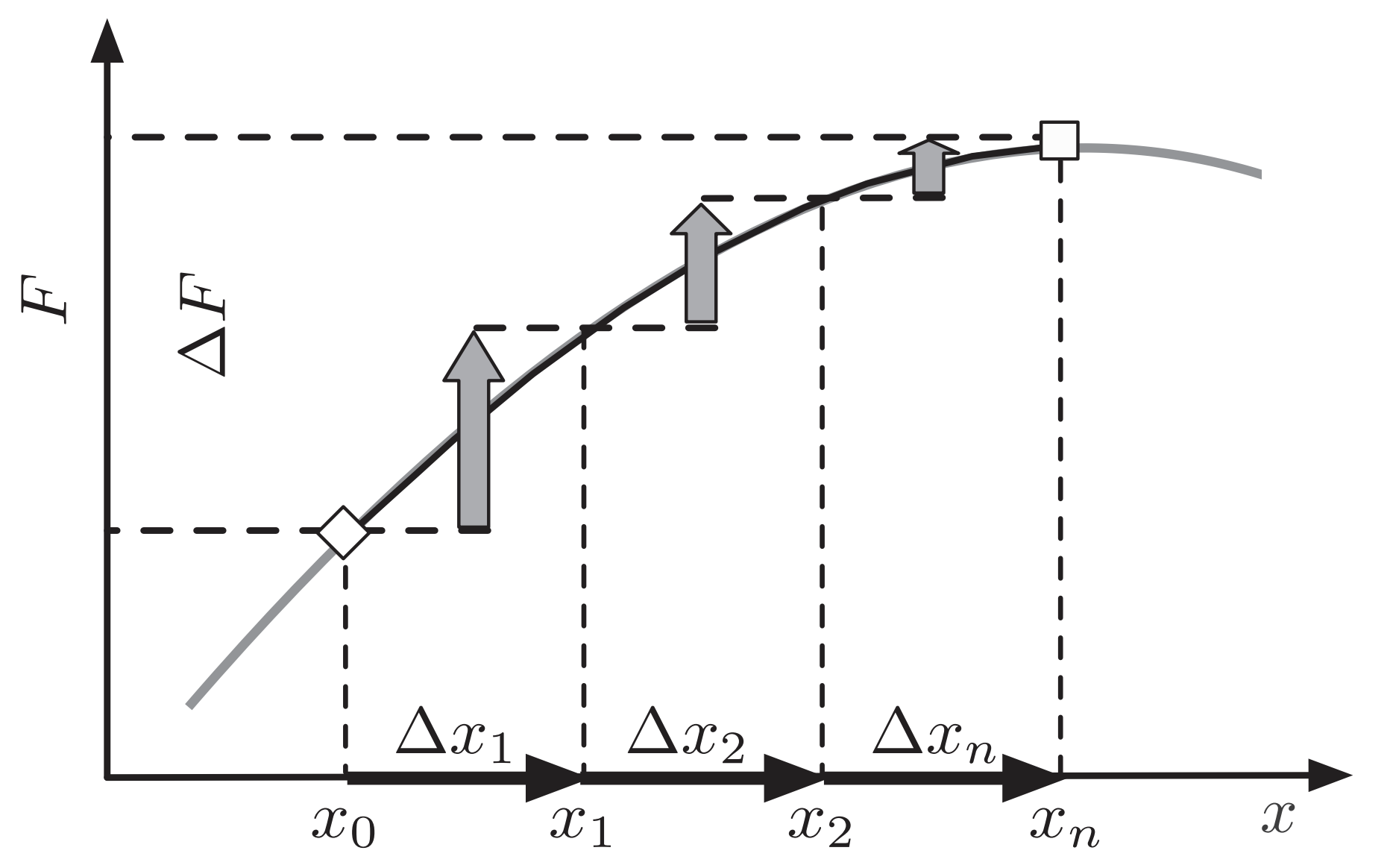
Fitness flux
Fitness flux is the rate of change of fitness across the population
Fitness flux $\phi(t) = \left( \sum_i \Delta x_i \, f_i \right) / \Delta t$
With constant variant fitness, fitness flux equals the rate of change of mean population fitness
Mean population fitness $\bar{f}(t) = \sum_i x_i(t) \, f_i$ Fitness flux $\phi(t) = \Delta \bar{f}(t) / \Delta t$
Defining terms
| Mean population fitness | $\bar{f}(t) = \sum_i x_i(t) \, f_i$ |
| Variance in fitness across population | $\mathrm{Var}[f(t)] = \sum_i x_i(t) \, (f_i - \bar{f}(t))^2$ |
| Velocity of mean population fitness | $\psi(t) = \Delta \bar{f}(t) / \Delta t$ |
| Fitness flux | $\phi(t) = \left( \sum_i \Delta x_i \, f_i \right) / \Delta t$ |
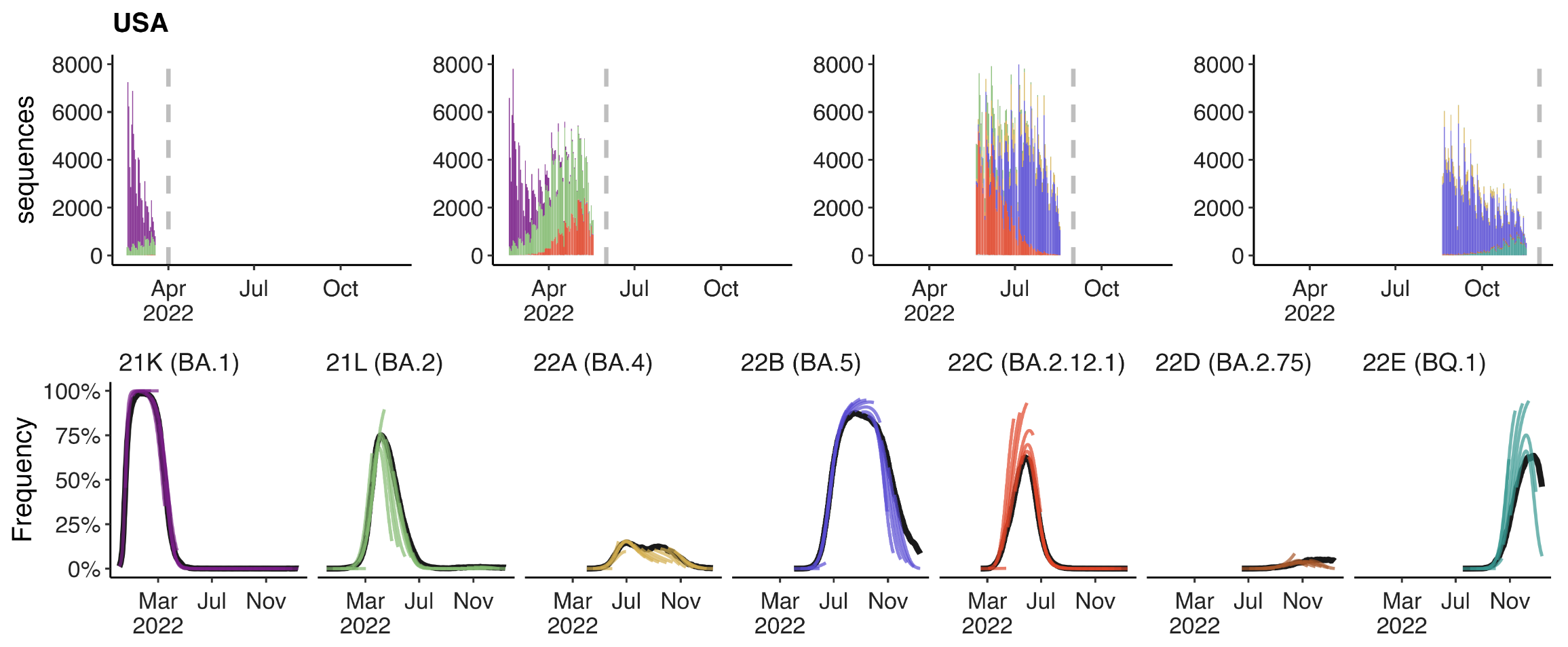
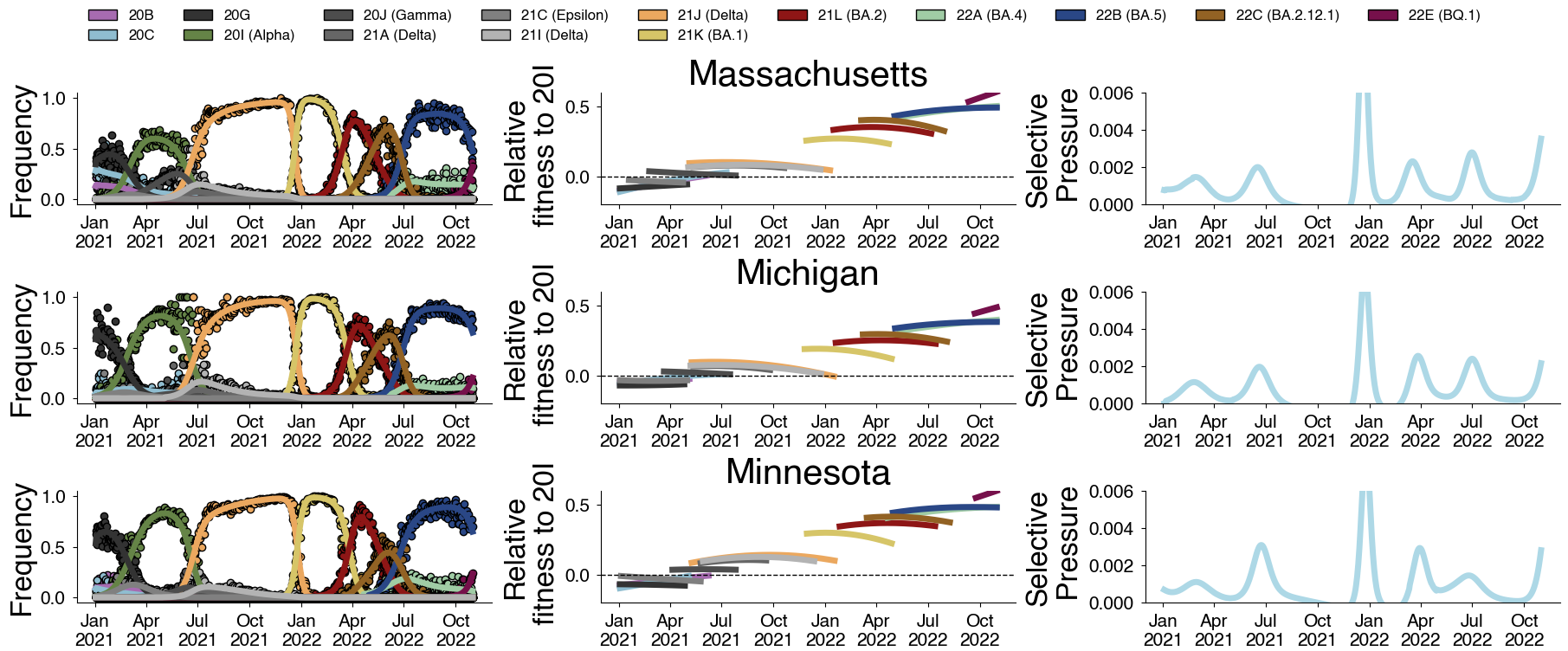
Clade-level frequency dynamics and MLR fits in sliding windows
Constant clade fitness within each window, USA data only, ignores within-clade fitness variation
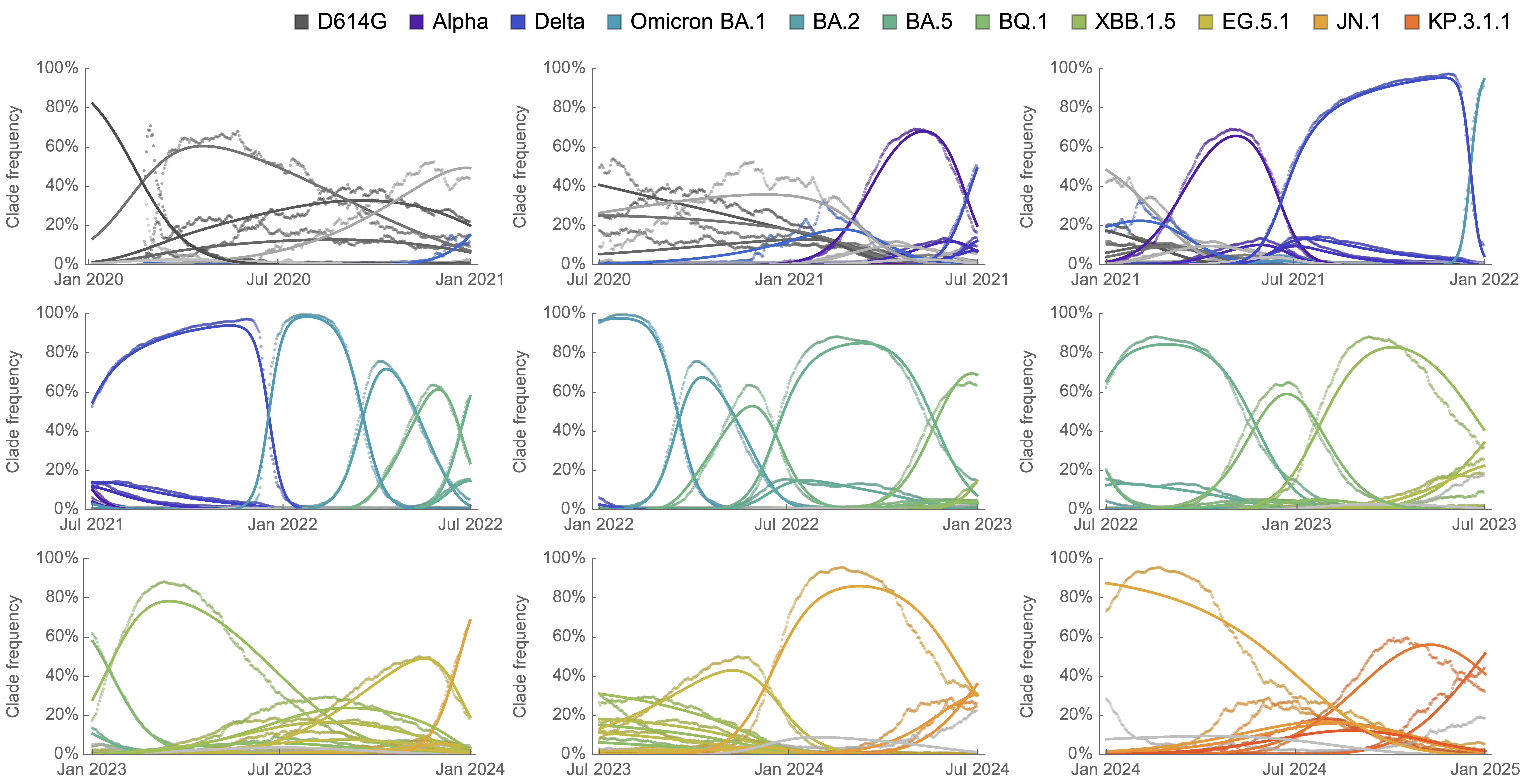
Fitness within each window is to an arbitrary baseline variant
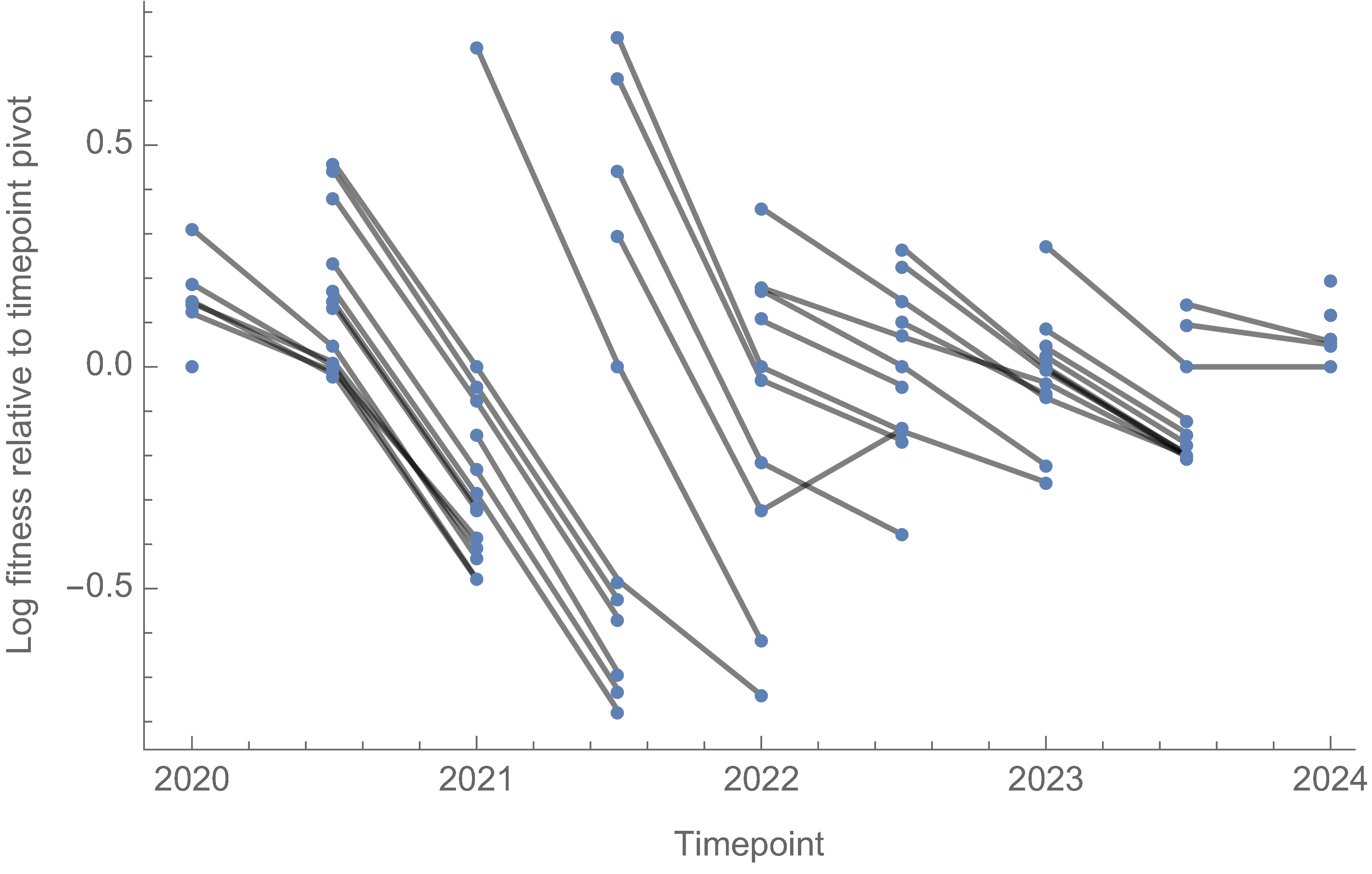
However, we can use ratio of variant fitnesses between adjacent timepoints to scaffold a combined set of fitness values
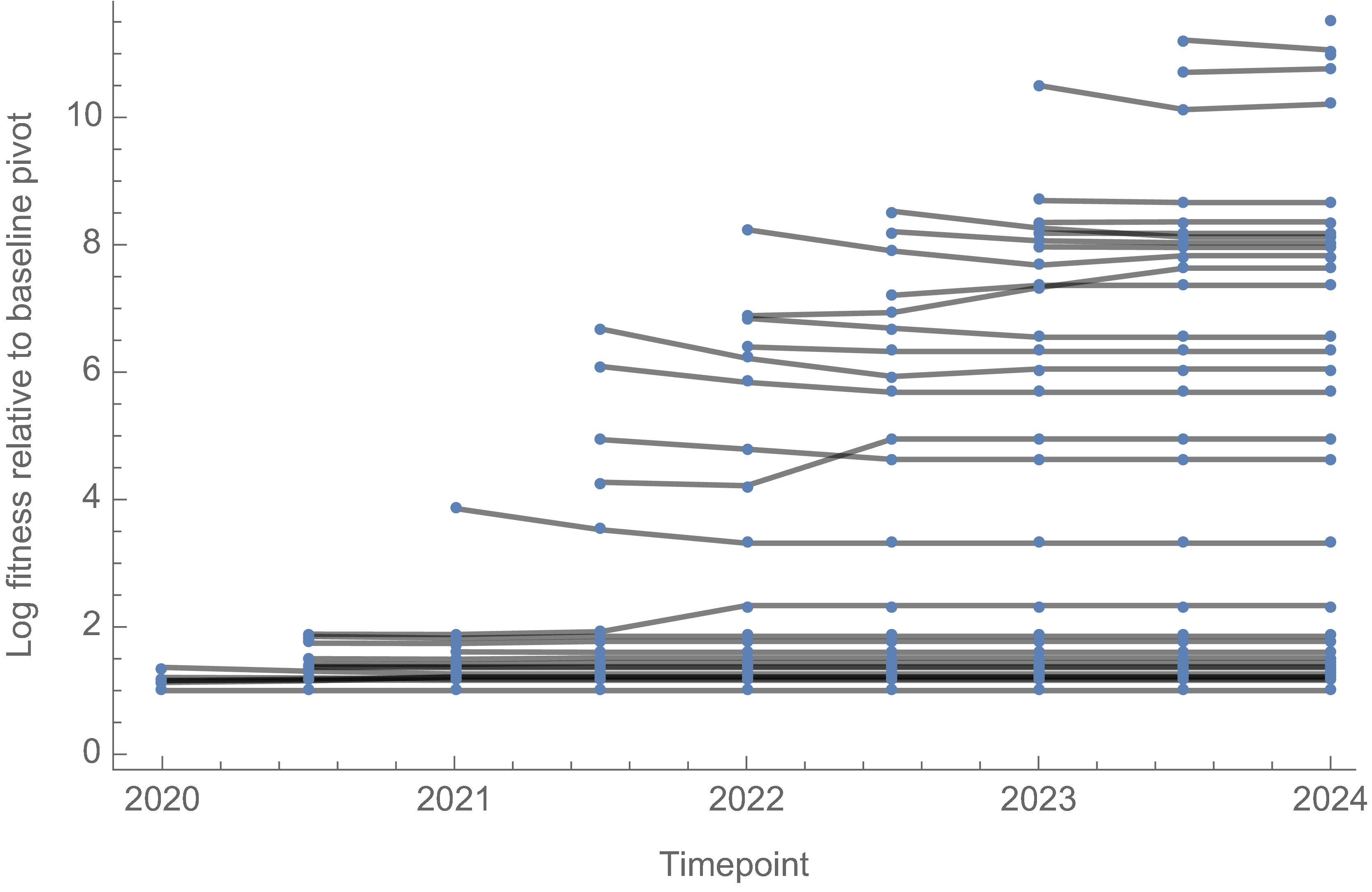
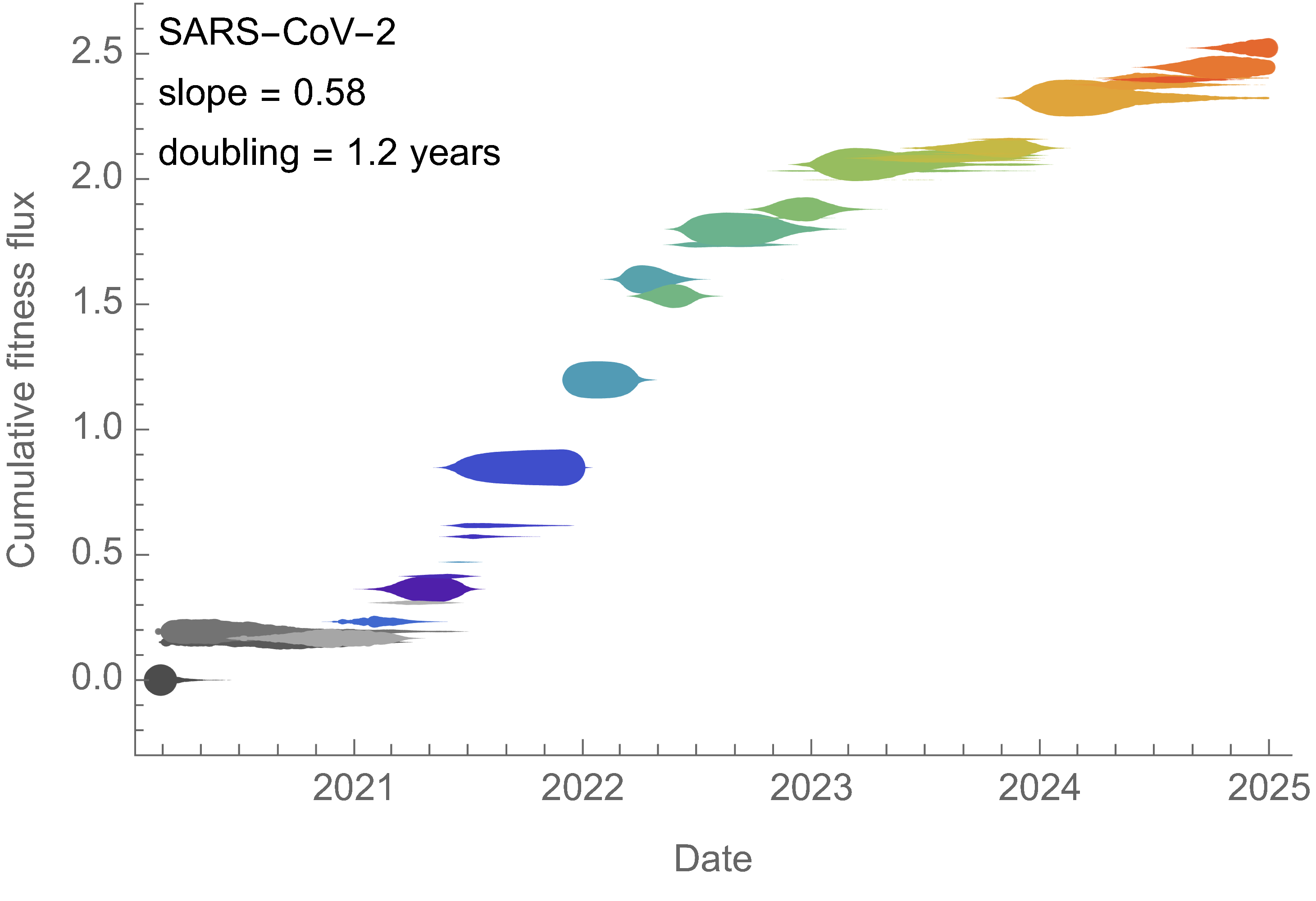
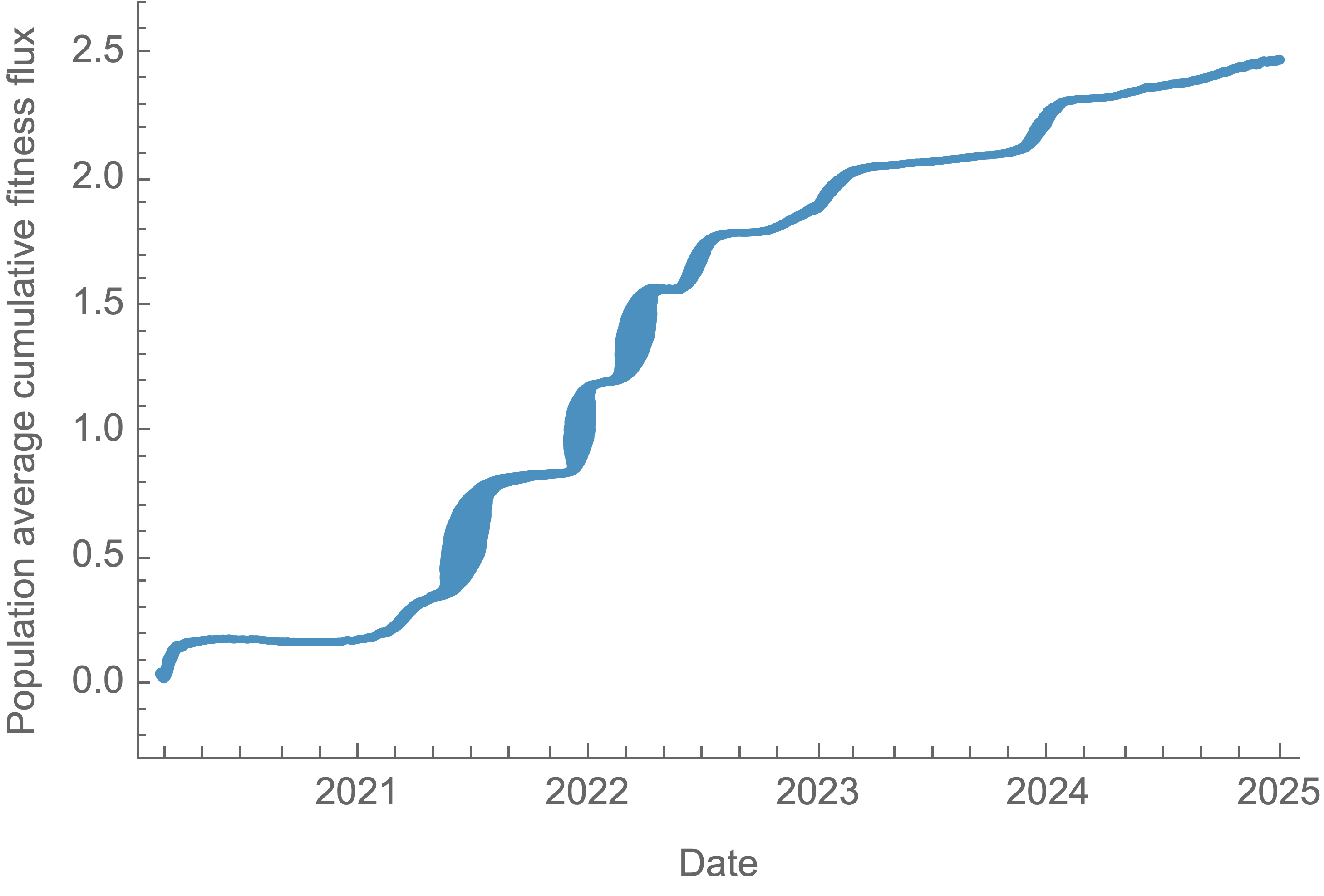
SAR-CoV-2 roughly doubled in fitness every year
Line thickness is proportional to variant frequency, 36 total variants
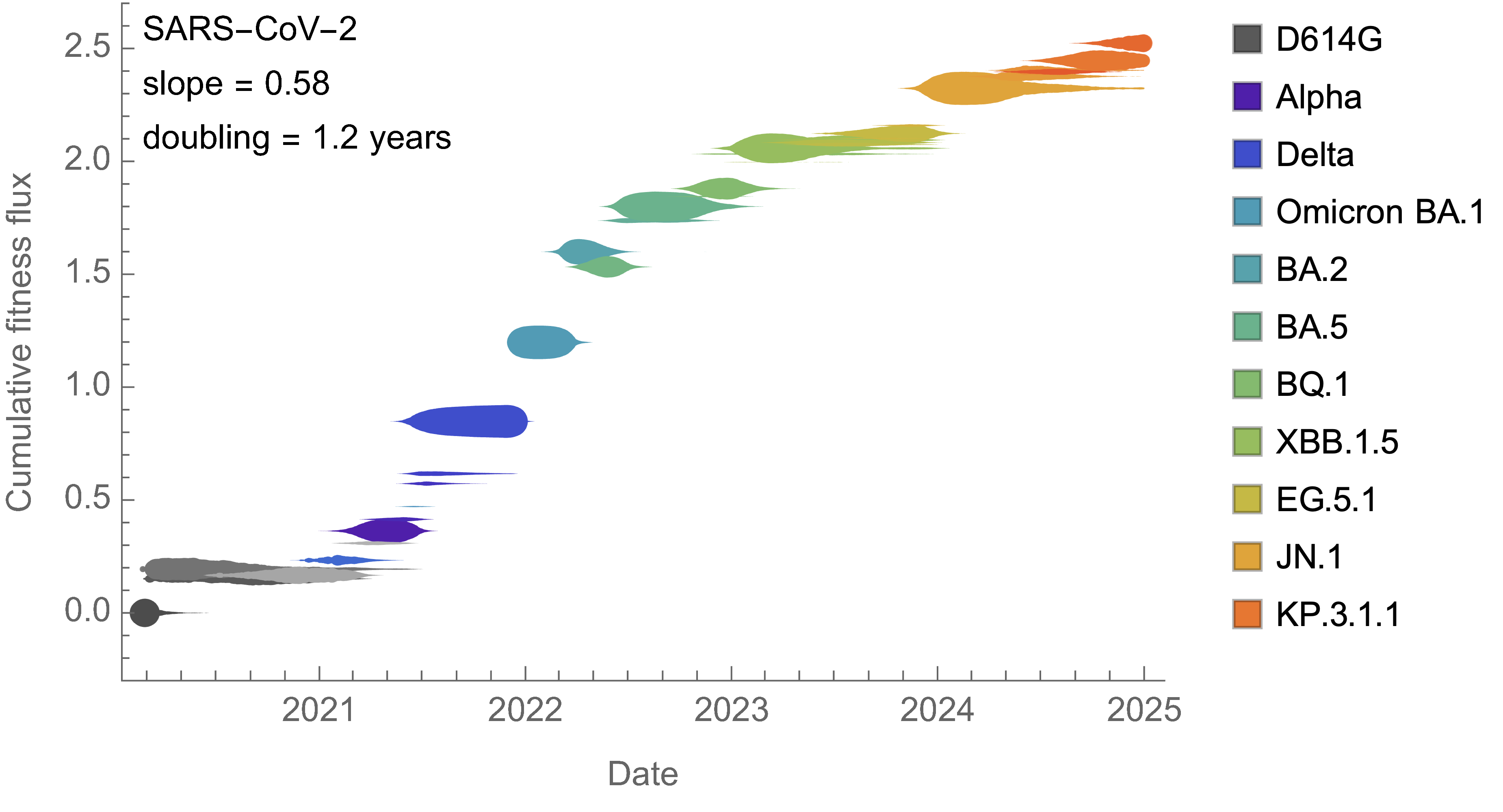
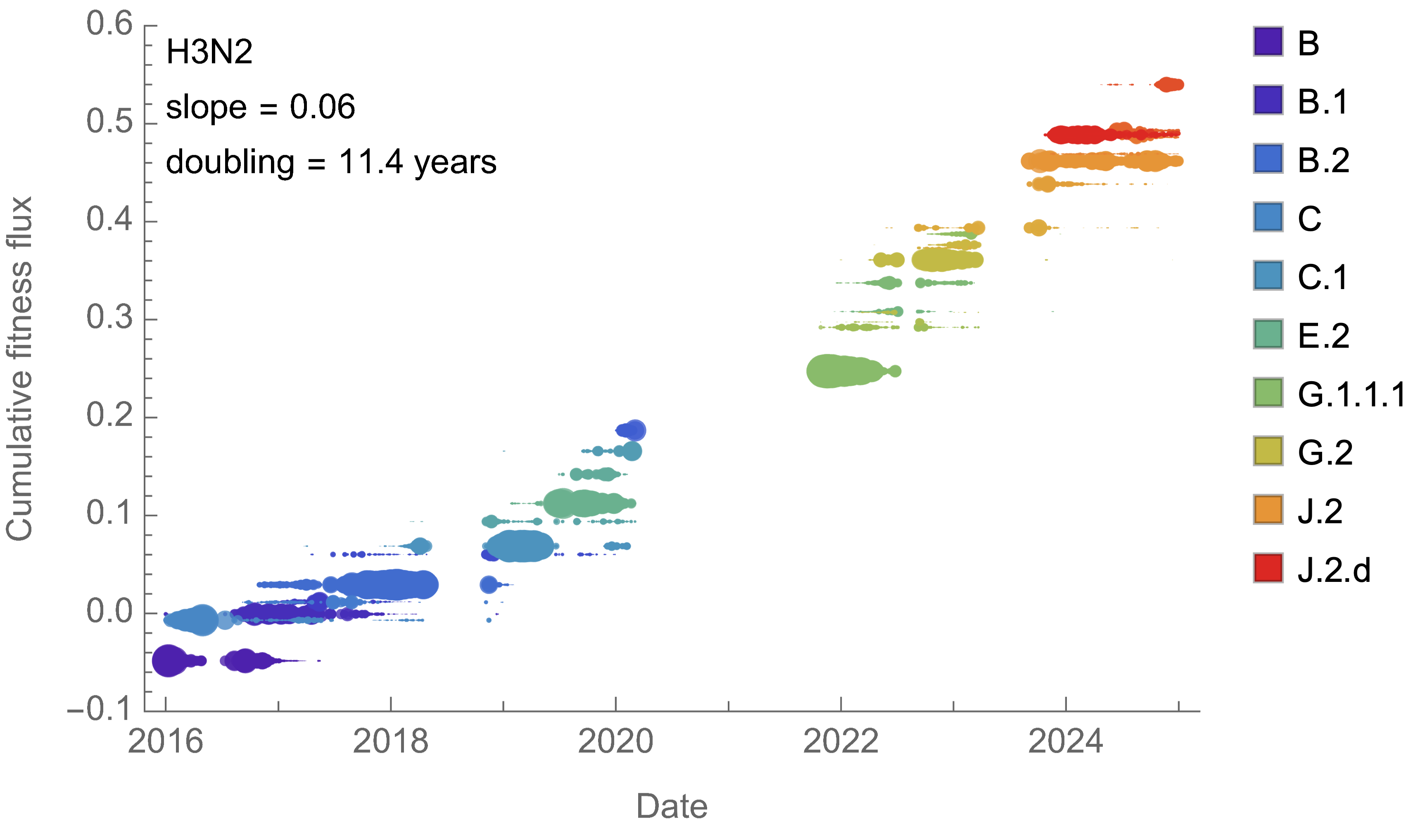
Analogous frequency dynamics and MLR fits for H3N2
Constant clade fitness within each window, USA data only, ignores within-clade fitness variation
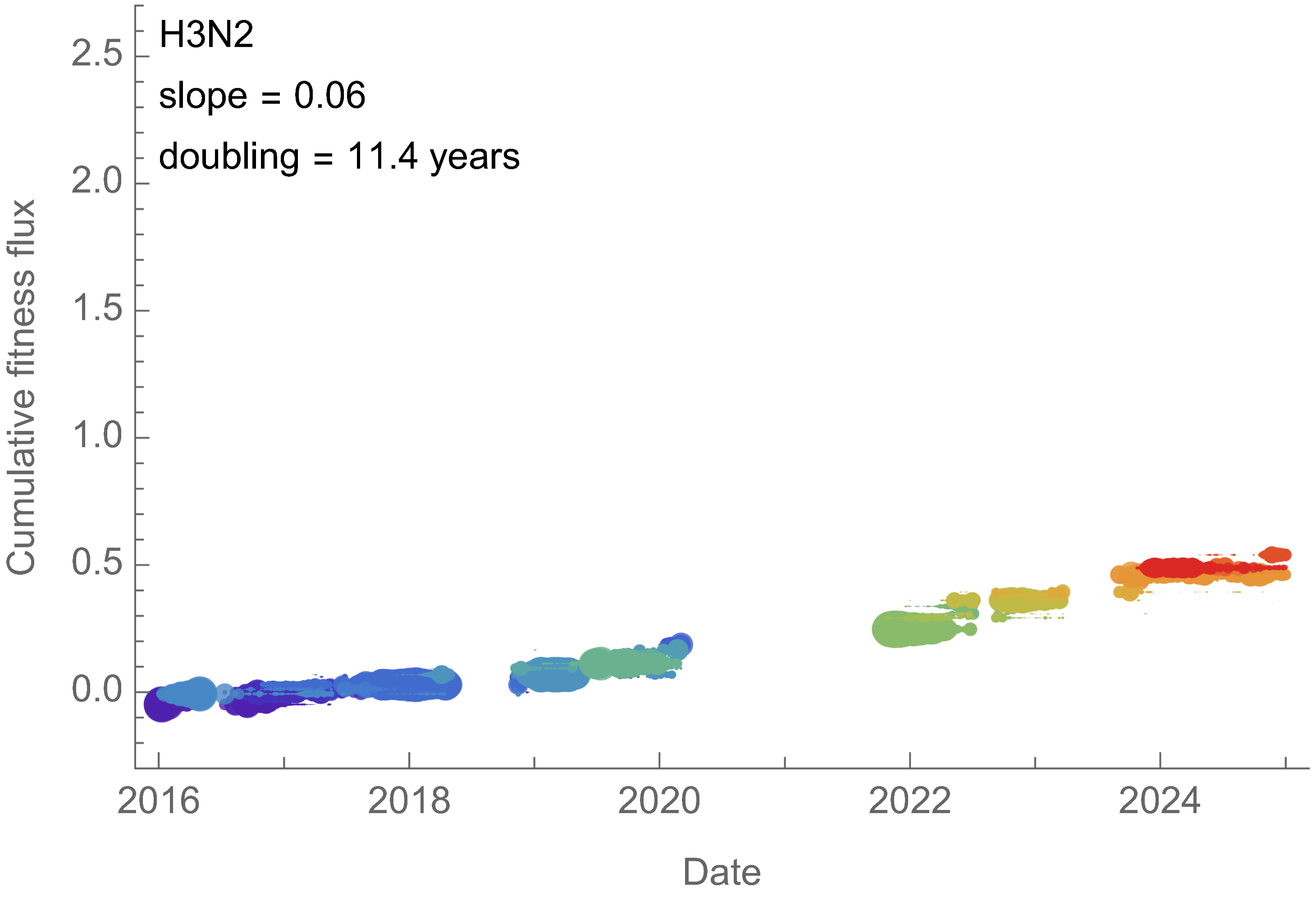
H3N2 roughly doubled in fitness every 10 years
Line thickness is proportional to variant frequency, 32 total variants
Dramatically faster fitness flux of SARS-CoV-2
Traveling fitness waves
Multistrain models produce traveling waves in antigenic space
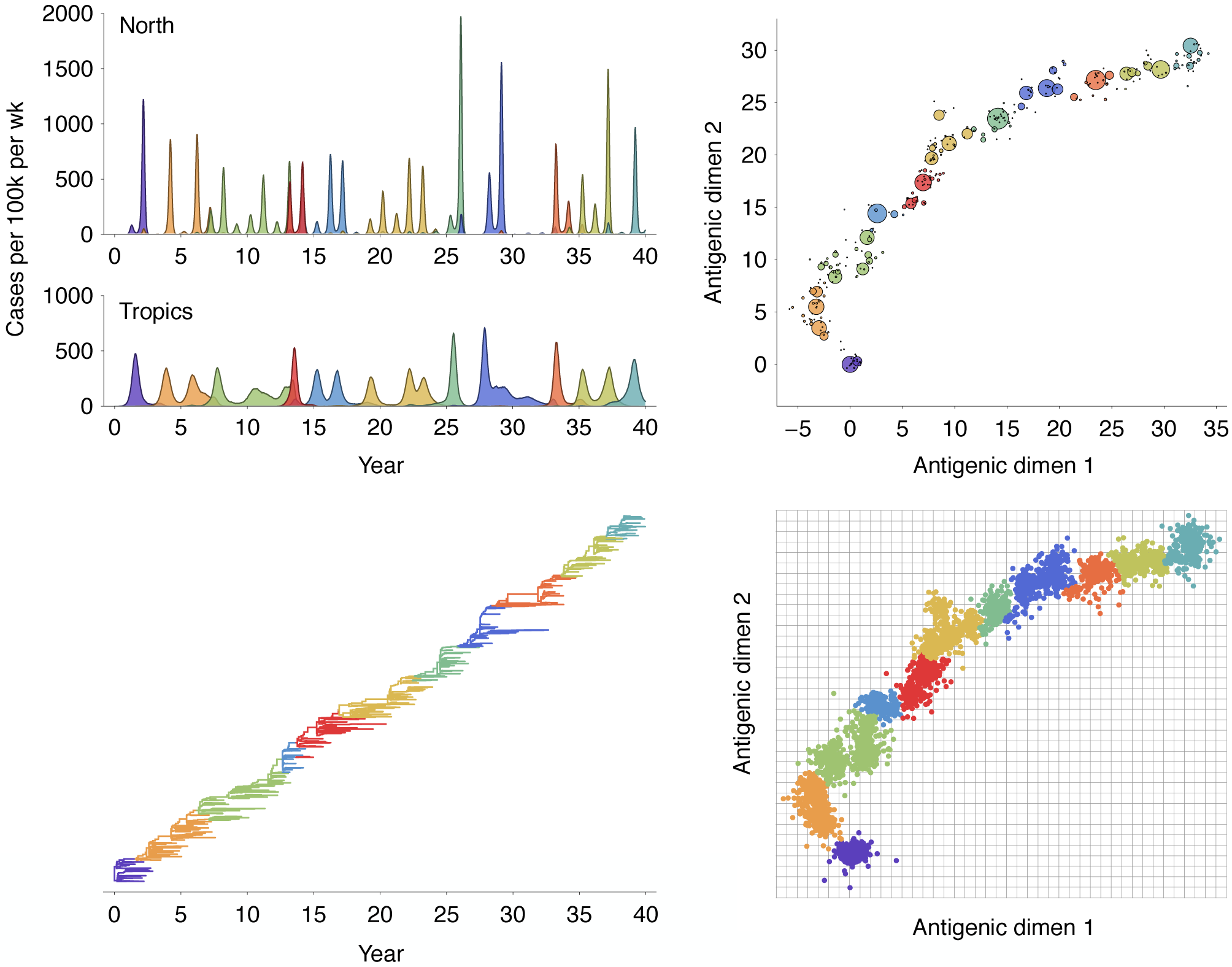
Many mutations of small effect create traveling fitness waves
Richard Neher and others have analytically characterized these waves
Diffusion constant $D = \mu \, \langle \delta^2 \rangle/2$, where the average $\langle \ldots \rangle$ is over the distribution of mutational effects $K(\delta)$
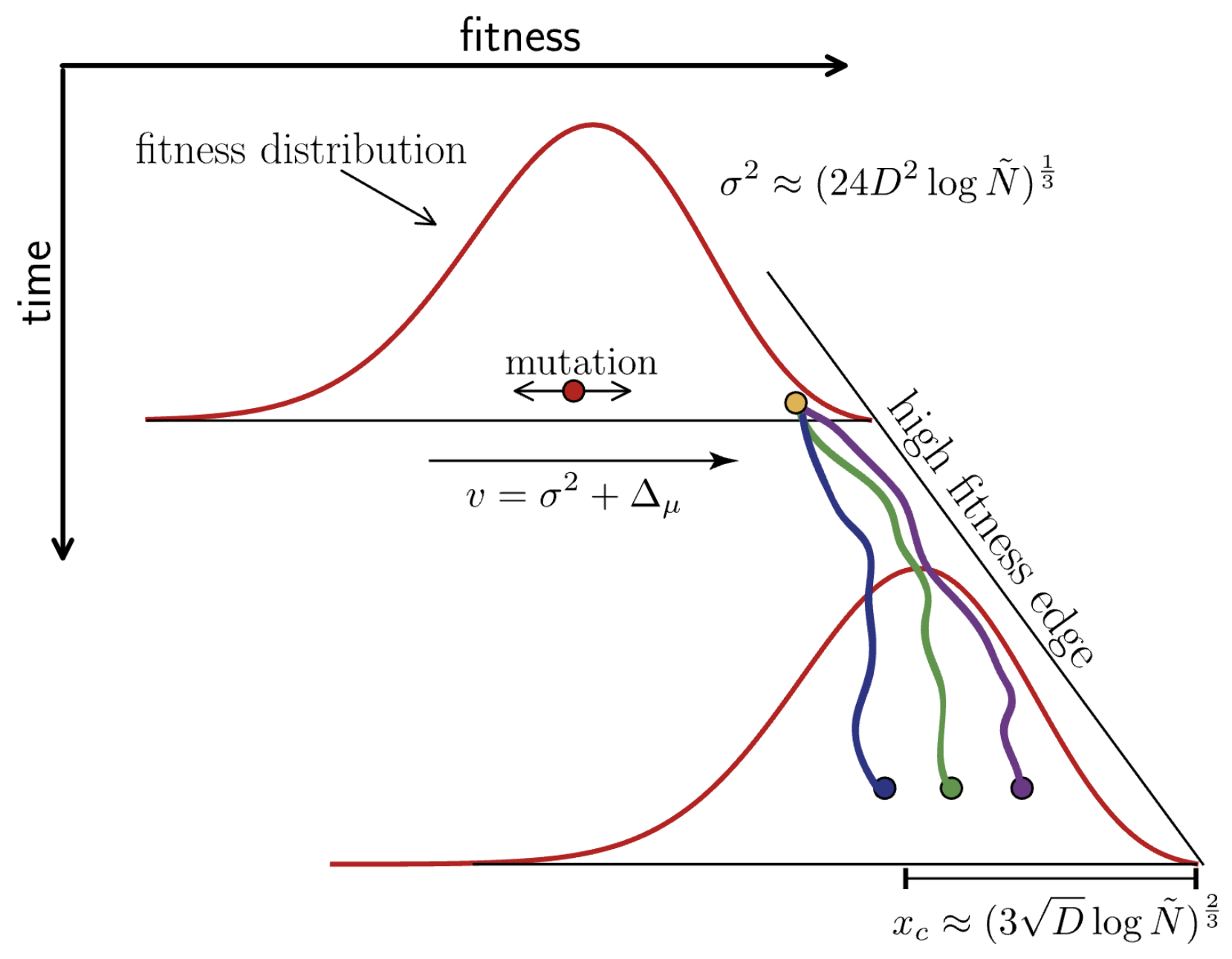
Using empirical frequencies and MLR fitness to characterize fitness wave
SARS-CoV-2
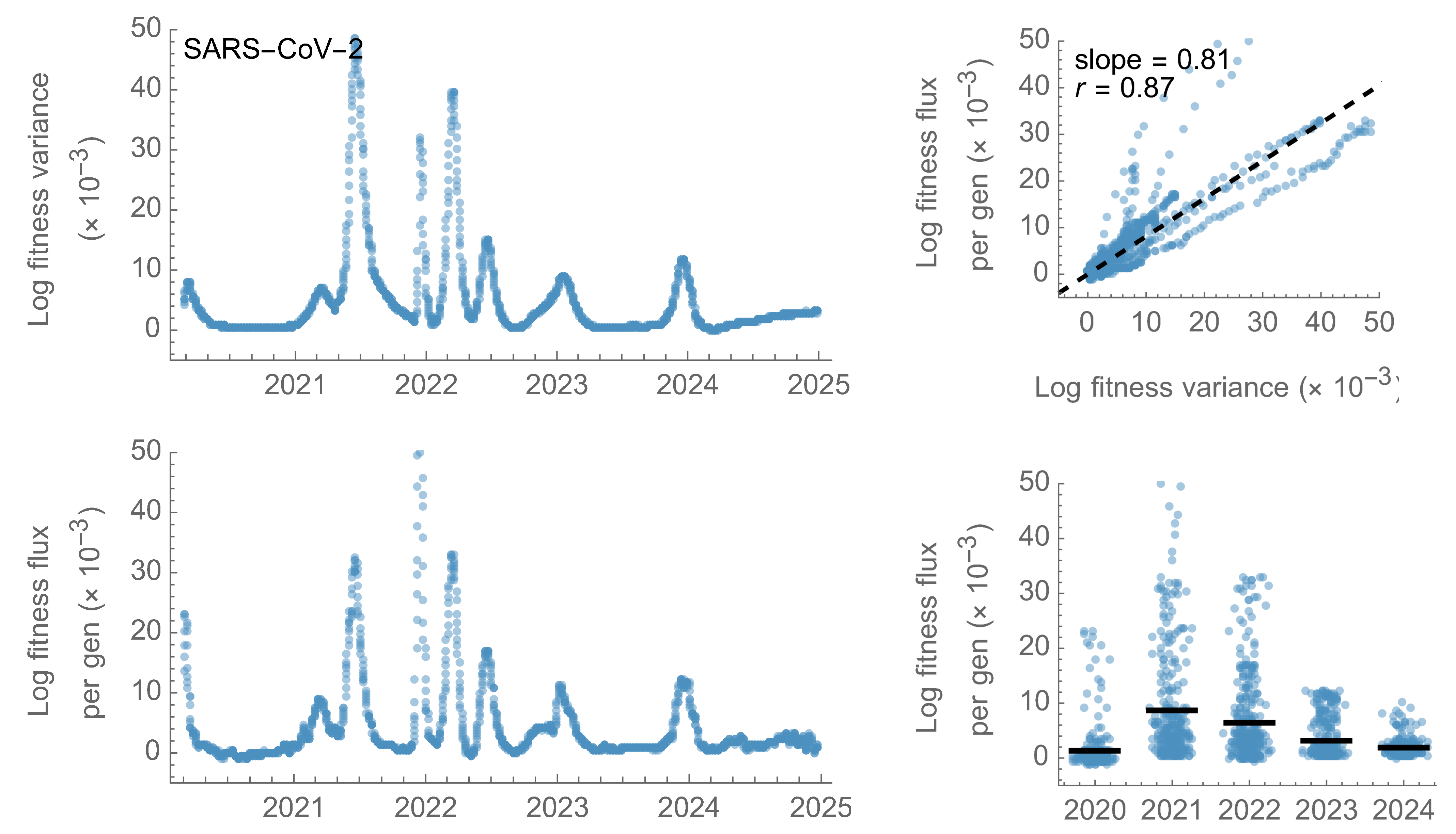
Fitness variance correlates well with fitness flux
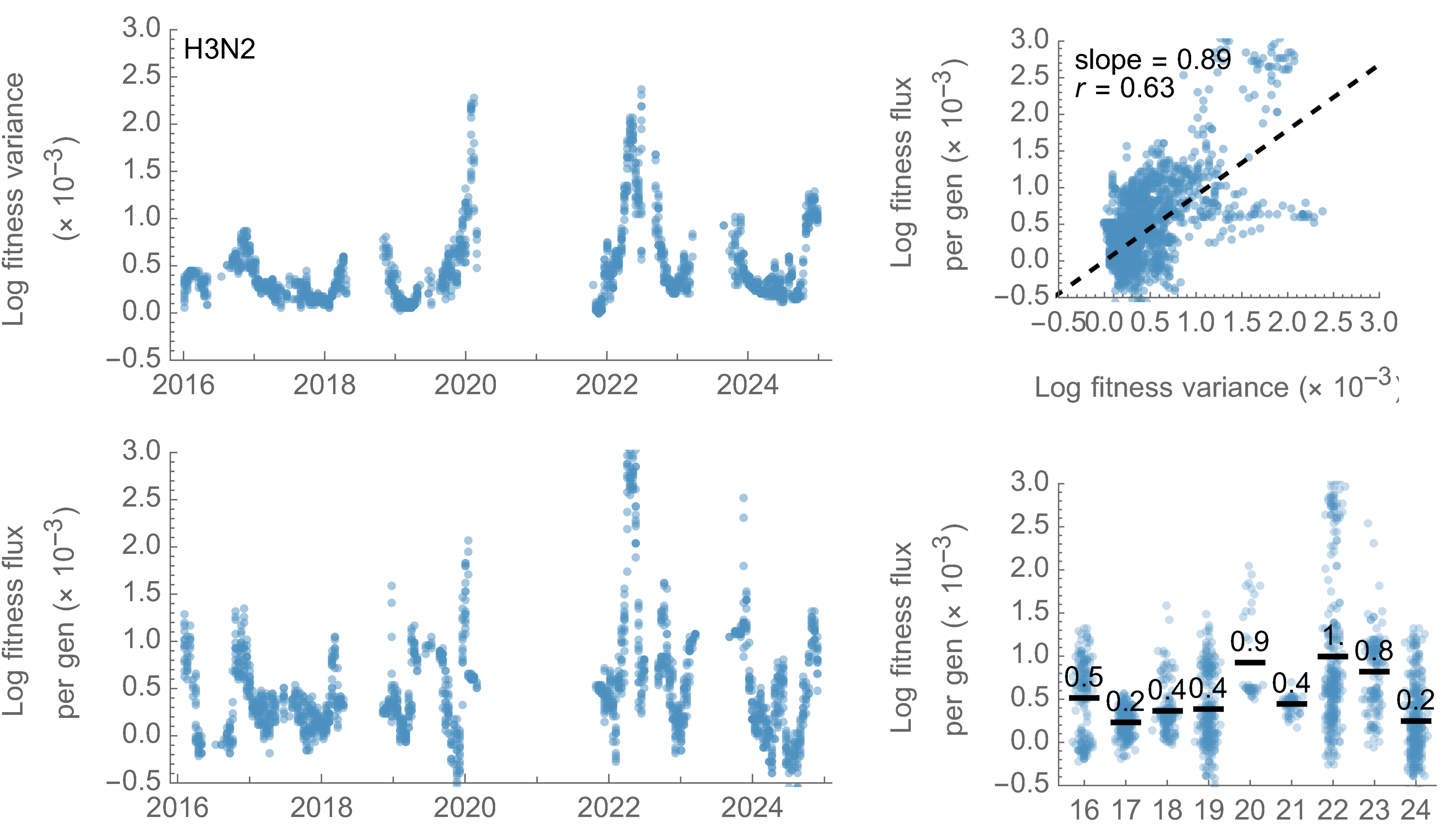
Fitness variance correlates well with fitness flux
This is a specific example of Fisher's fundemental theorem
"The rate of increase in fitness of any organism at any time is equal to
its genetic variance in fitness at that time," ie
$$\frac{d\bar{f}}{dt} = Var(f)$$
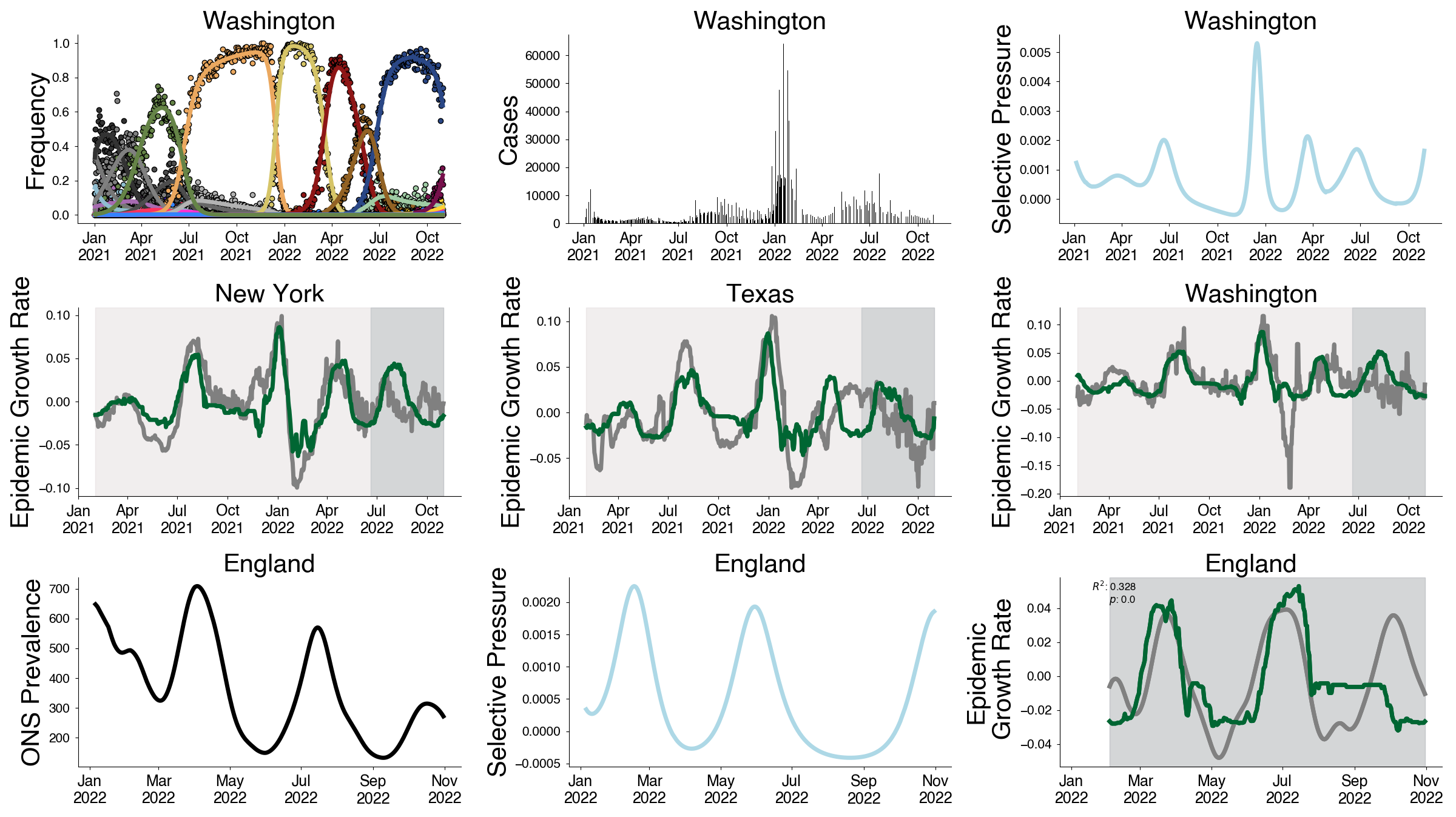
Fitness flux drives infection incidence
Selective pressure metric
$$\psi(t) = \Delta \bar{f}(t) / \Delta t = \mathbb{E}_{x(t)} \left[ \frac{d f_i}{d t}\right] + \mathbb{V}_{x(t)}[f_{i}]$$
Selective pressure predicts epidemic growth rate
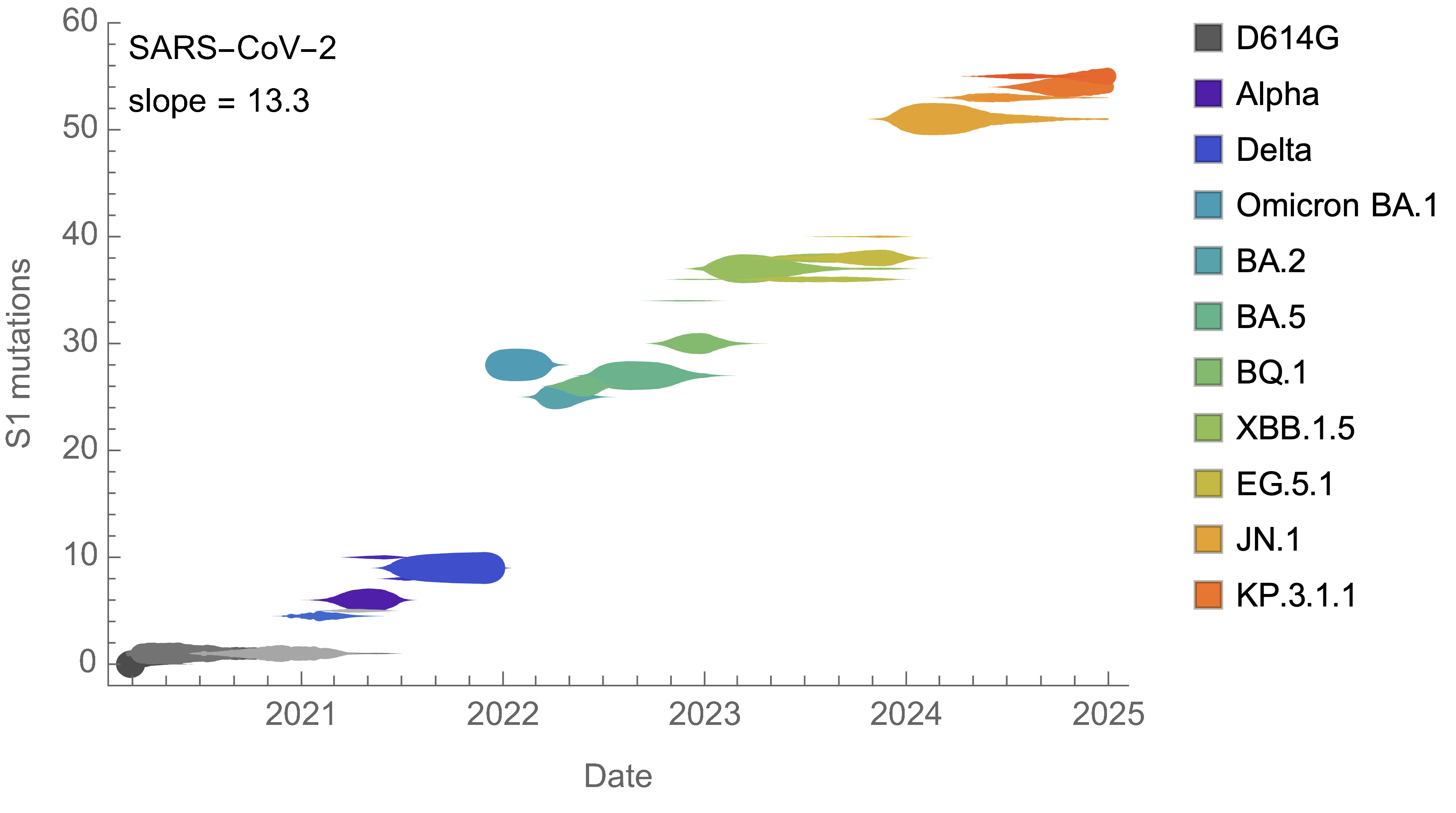
Mutational fitness effects
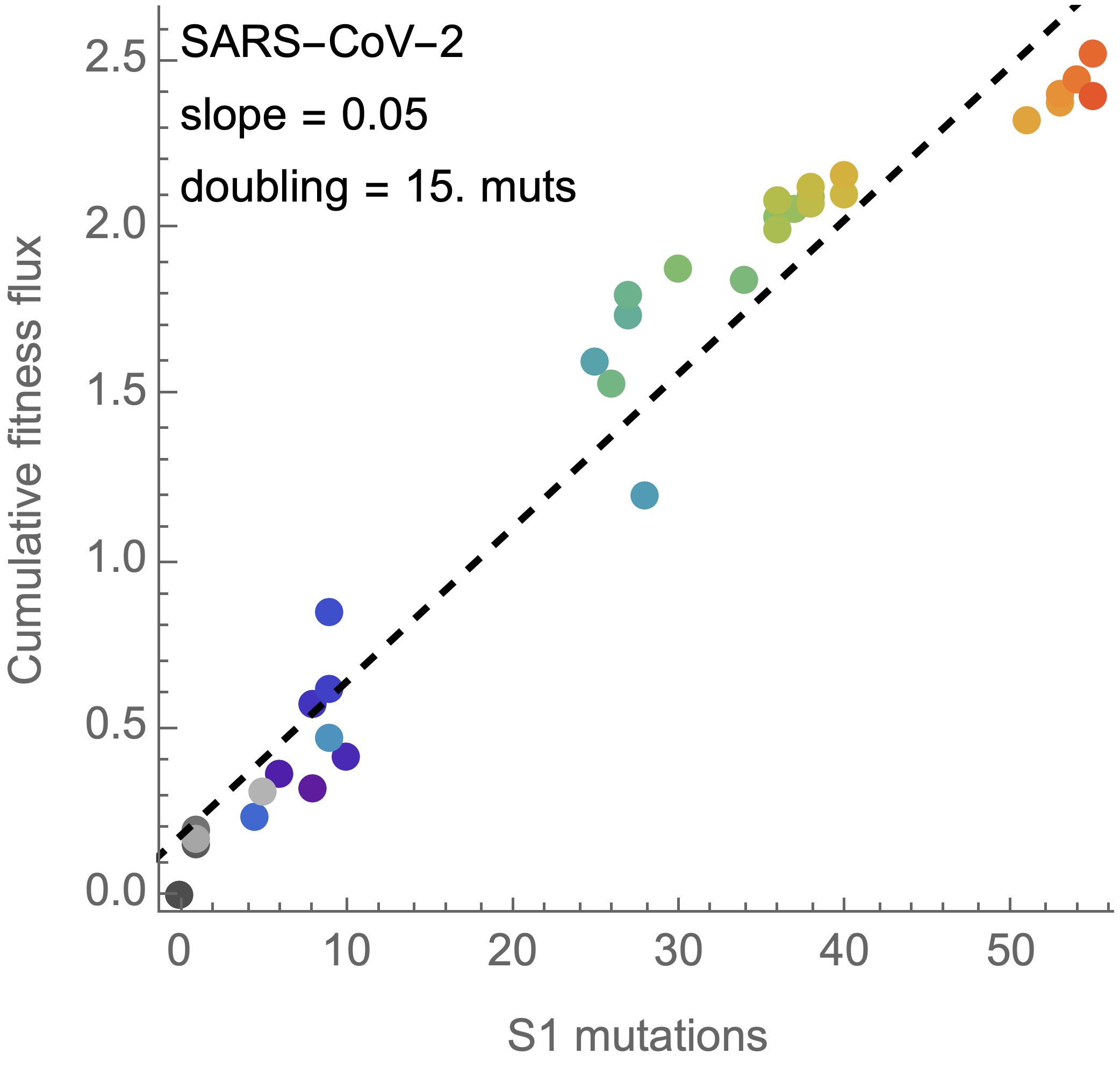
On average, SARS-CoV-2 accumulated 13-14 spike S1 mutations every year
15 mutations to spike S1 resulted in a doubling of fitness
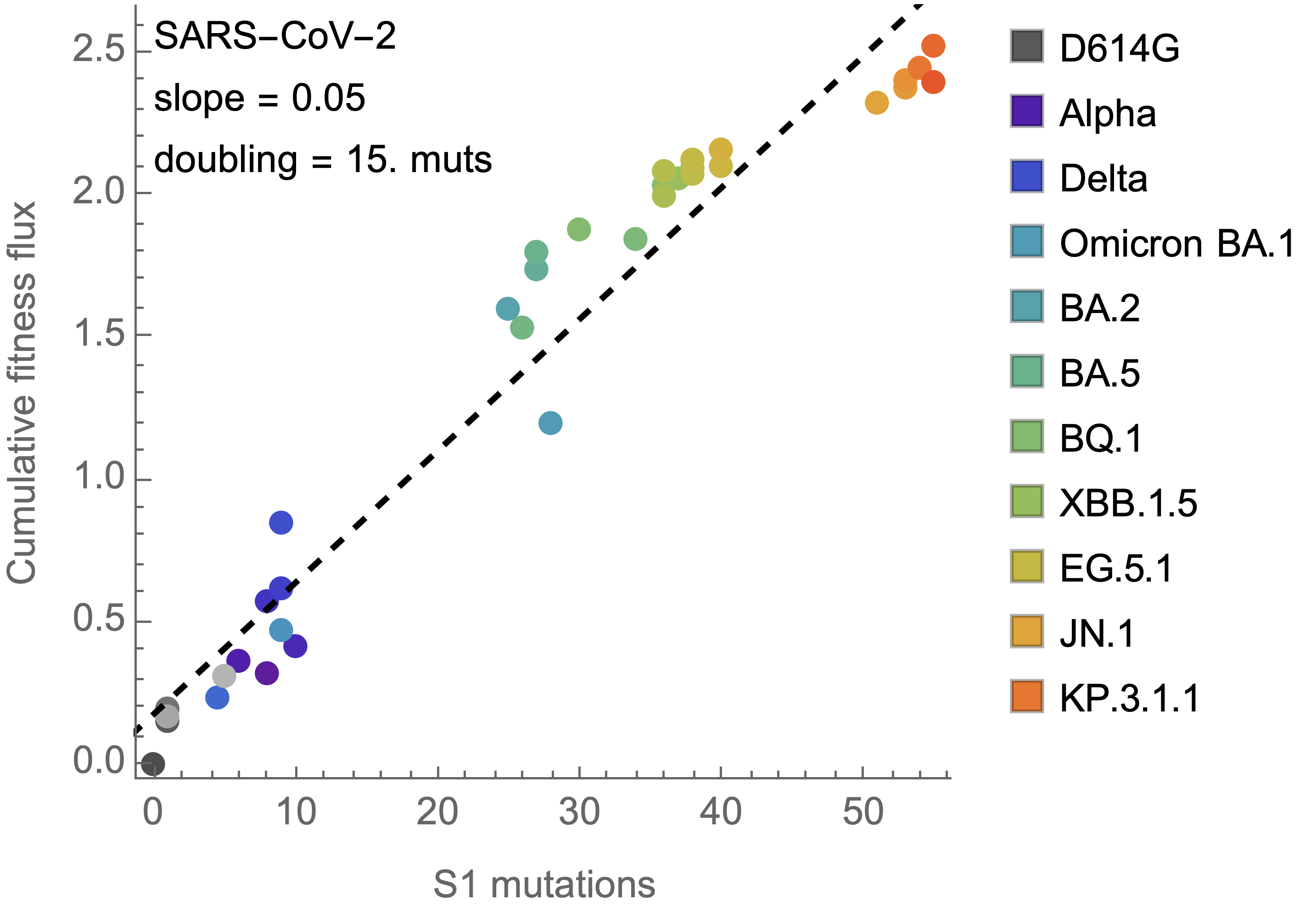
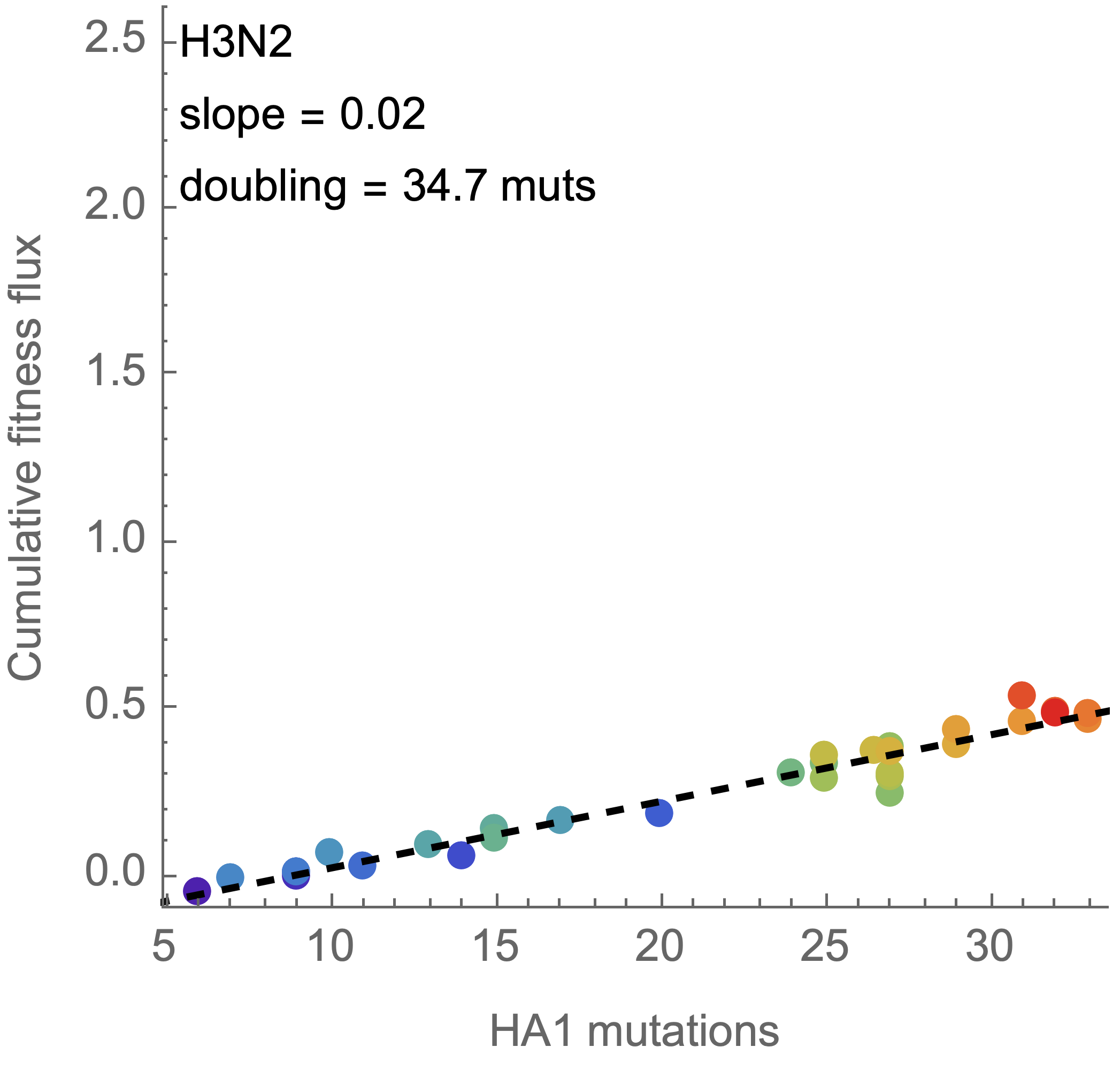
Again, we see a substantial difference with influenza H3N2
Fitness effects of fixed mutations are ~0.05 for SARS-CoV-2 and ~0.02 for H3N2
Switch to analyzing differences between parent/child lineages
Collapsed to 367 Pango lineages with at least 1000 sequence counts in the US
Most Pango branches have 0-1 spike mutations and change log fitness by ±0.1
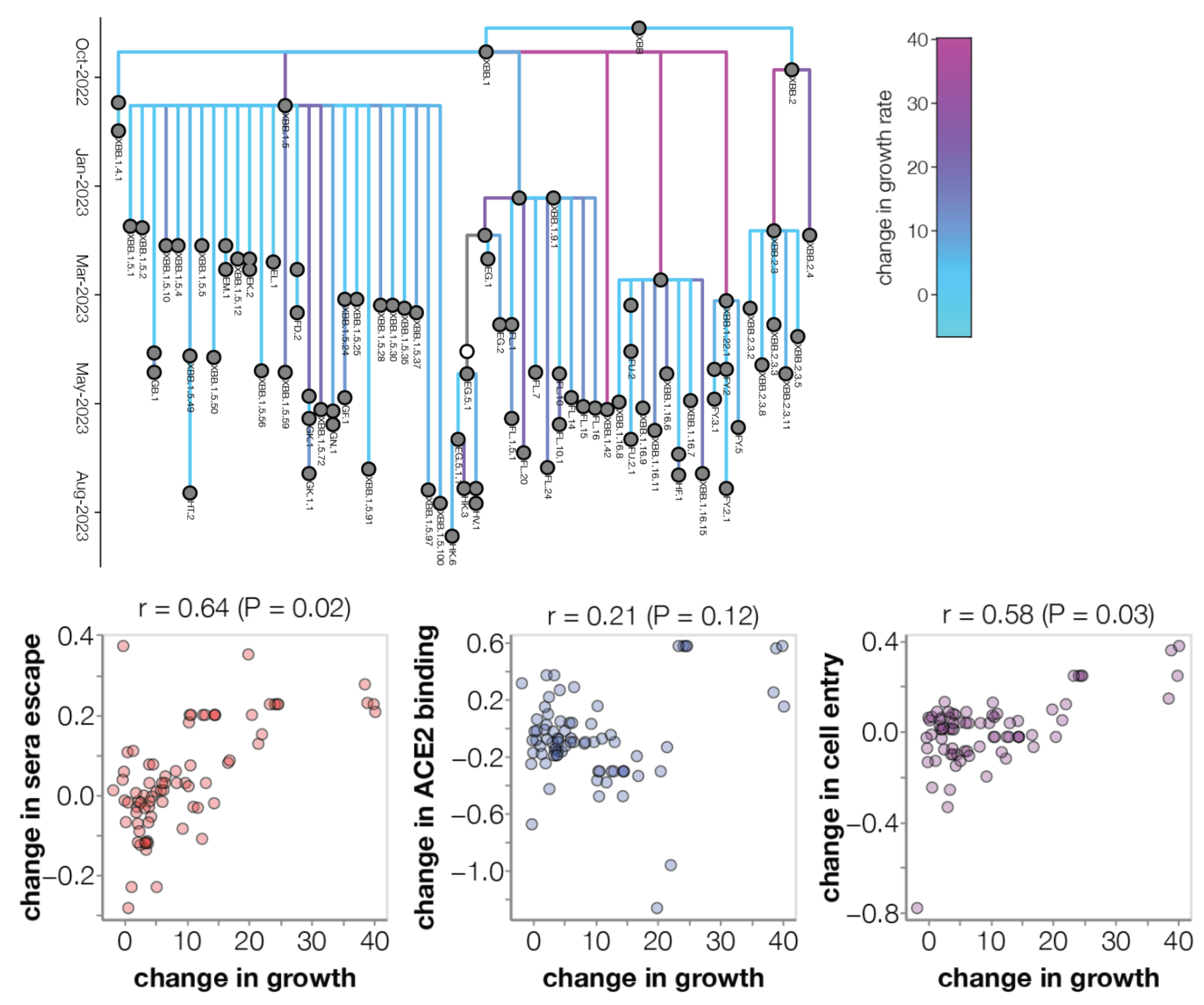
Spike mutations tend to increase fitness
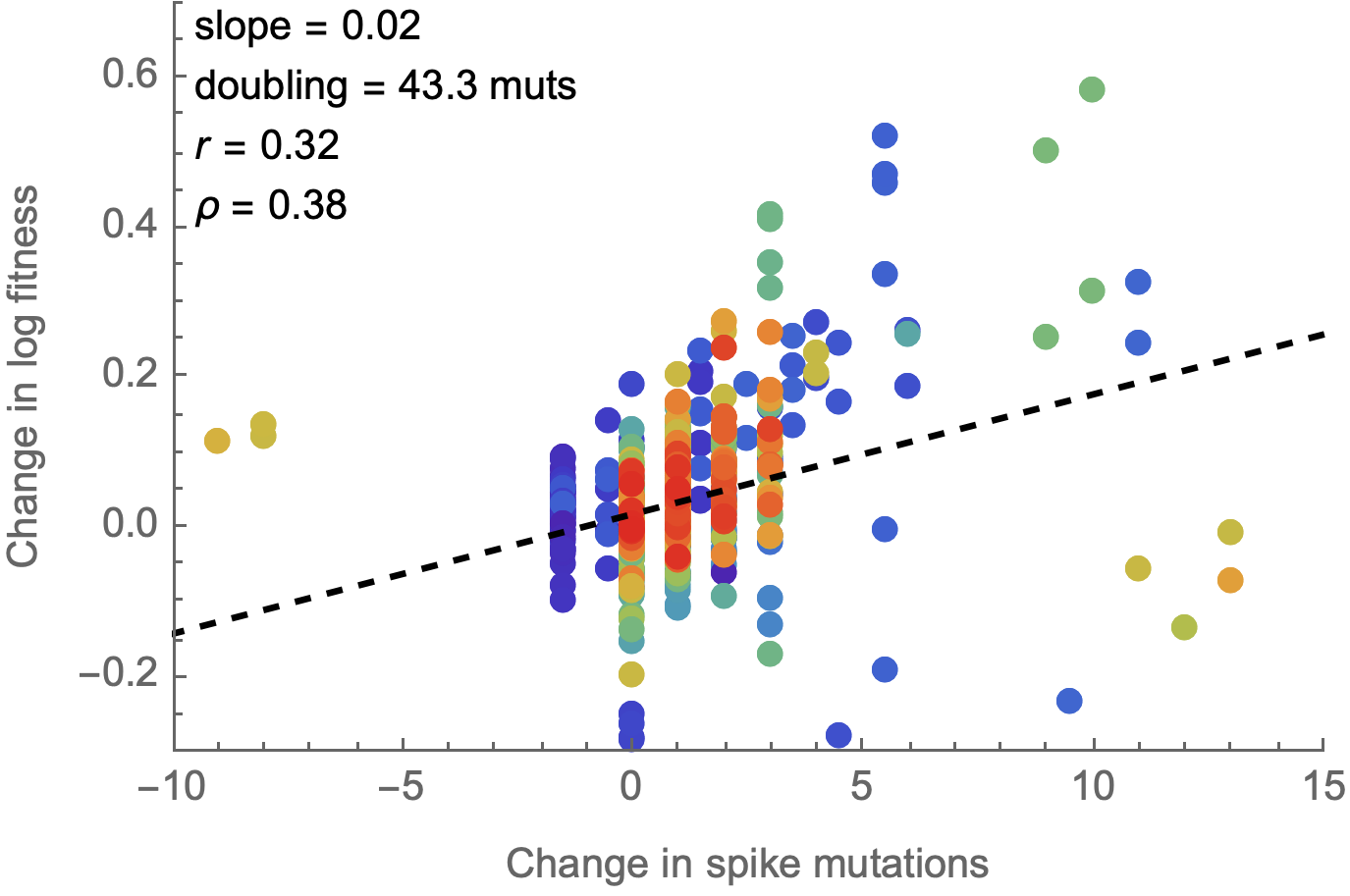
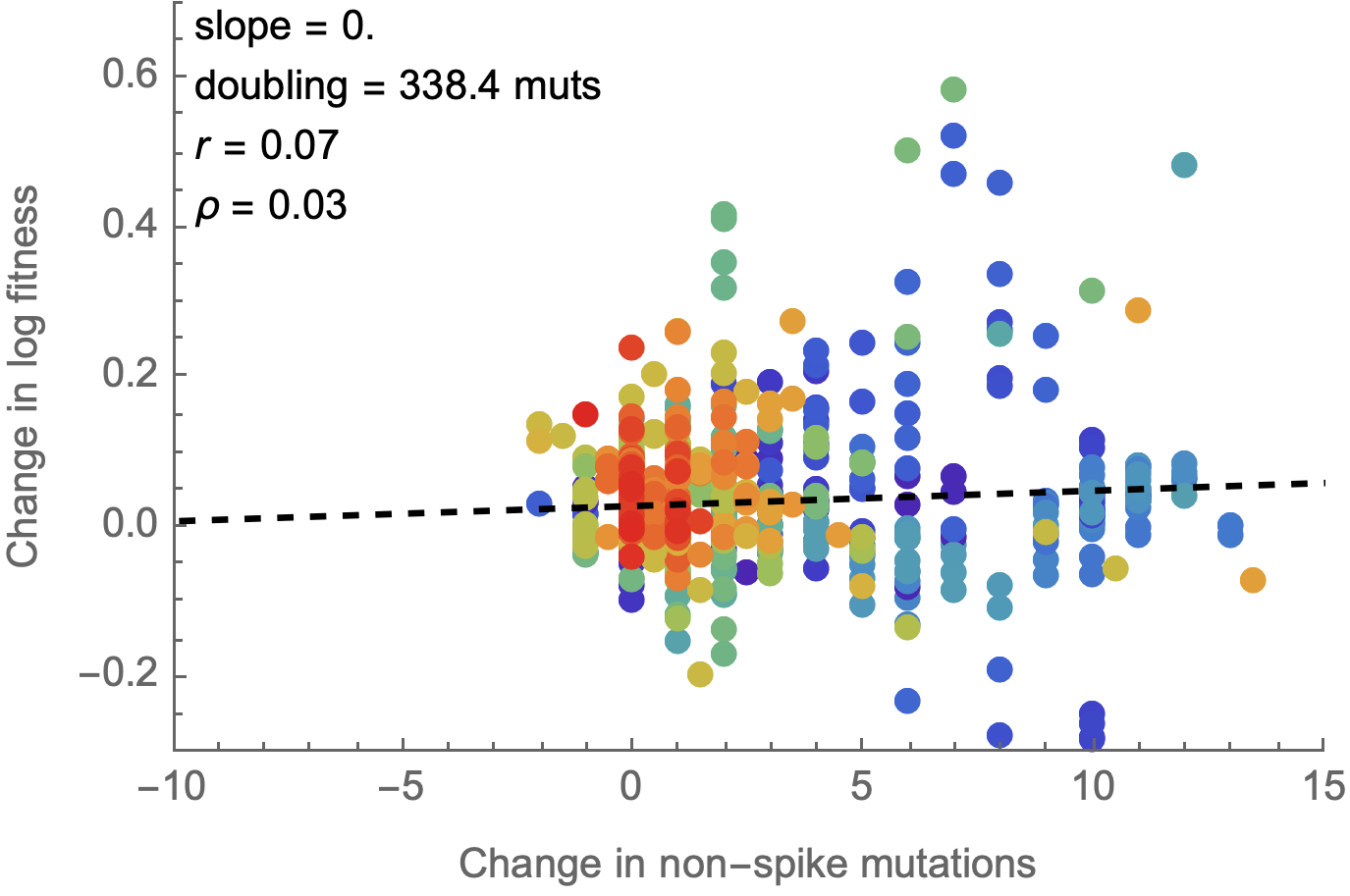
Non-spike mutations do not impact fitness on average
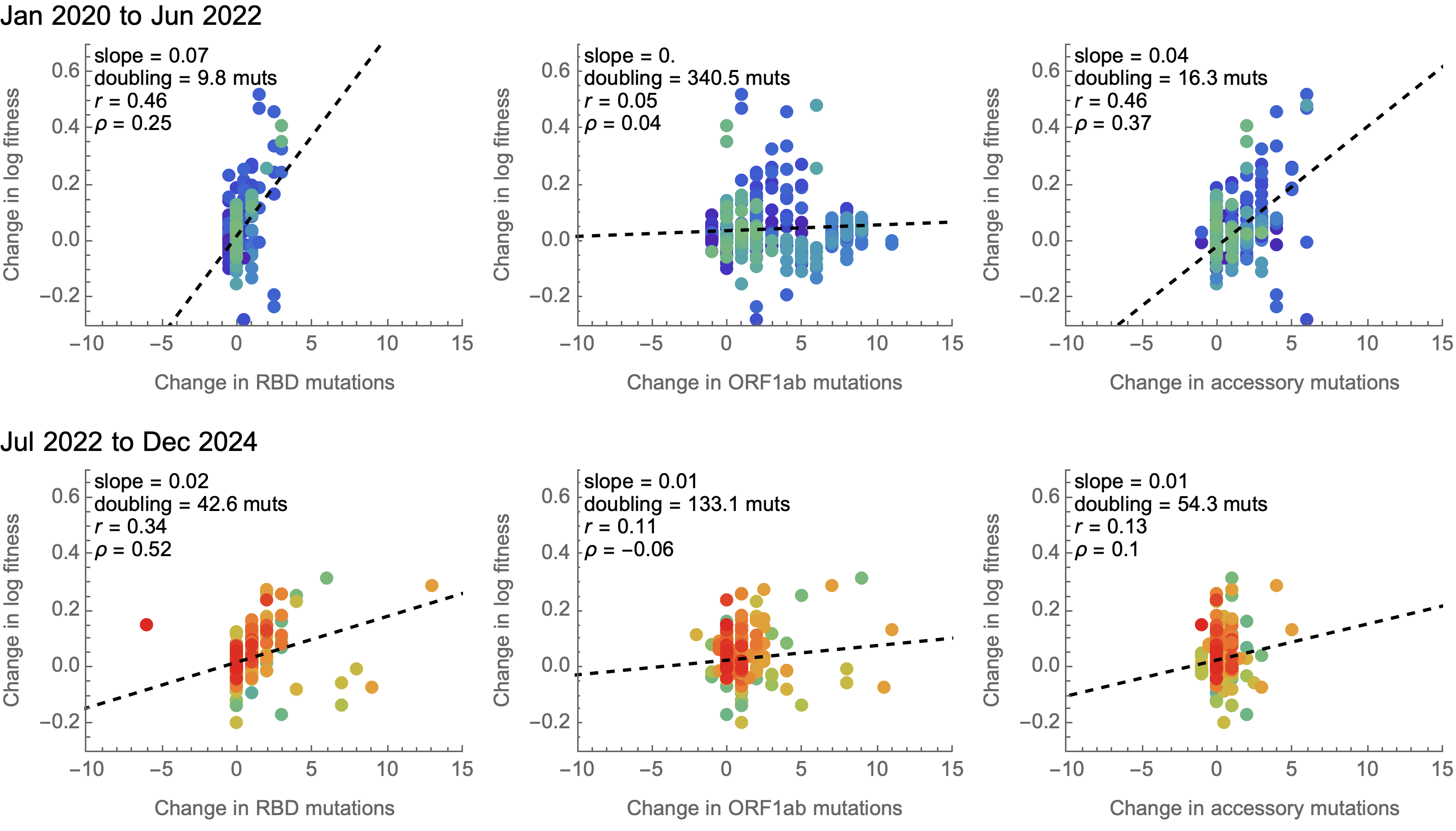
Looking across the genome shows that spike is the focus for positive selection, but accessory genes have some signal
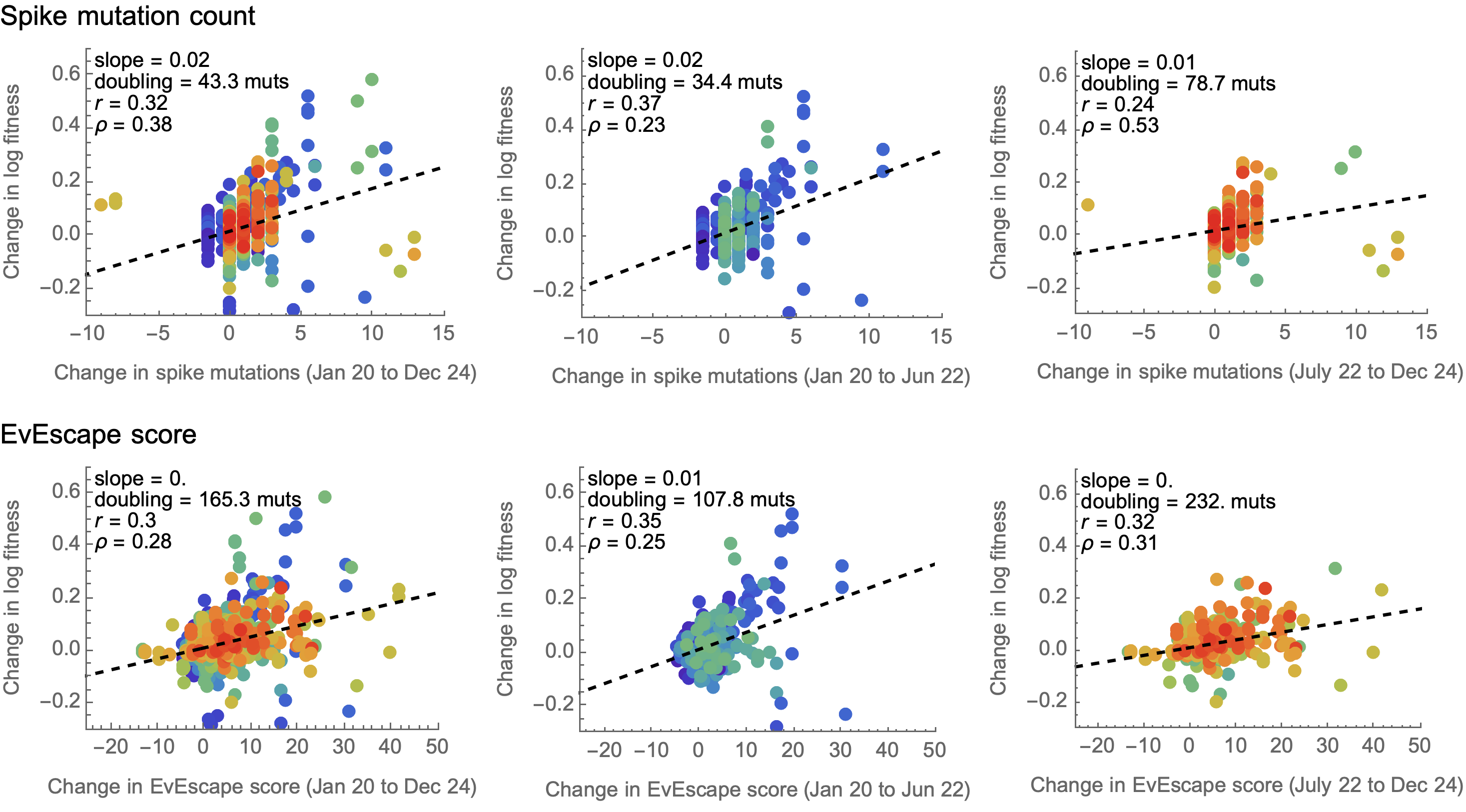
Some attentuation of fitness effects over time
Framework to compare predictors of fitness
Simple linear model to combine predictors into a fitness estimate
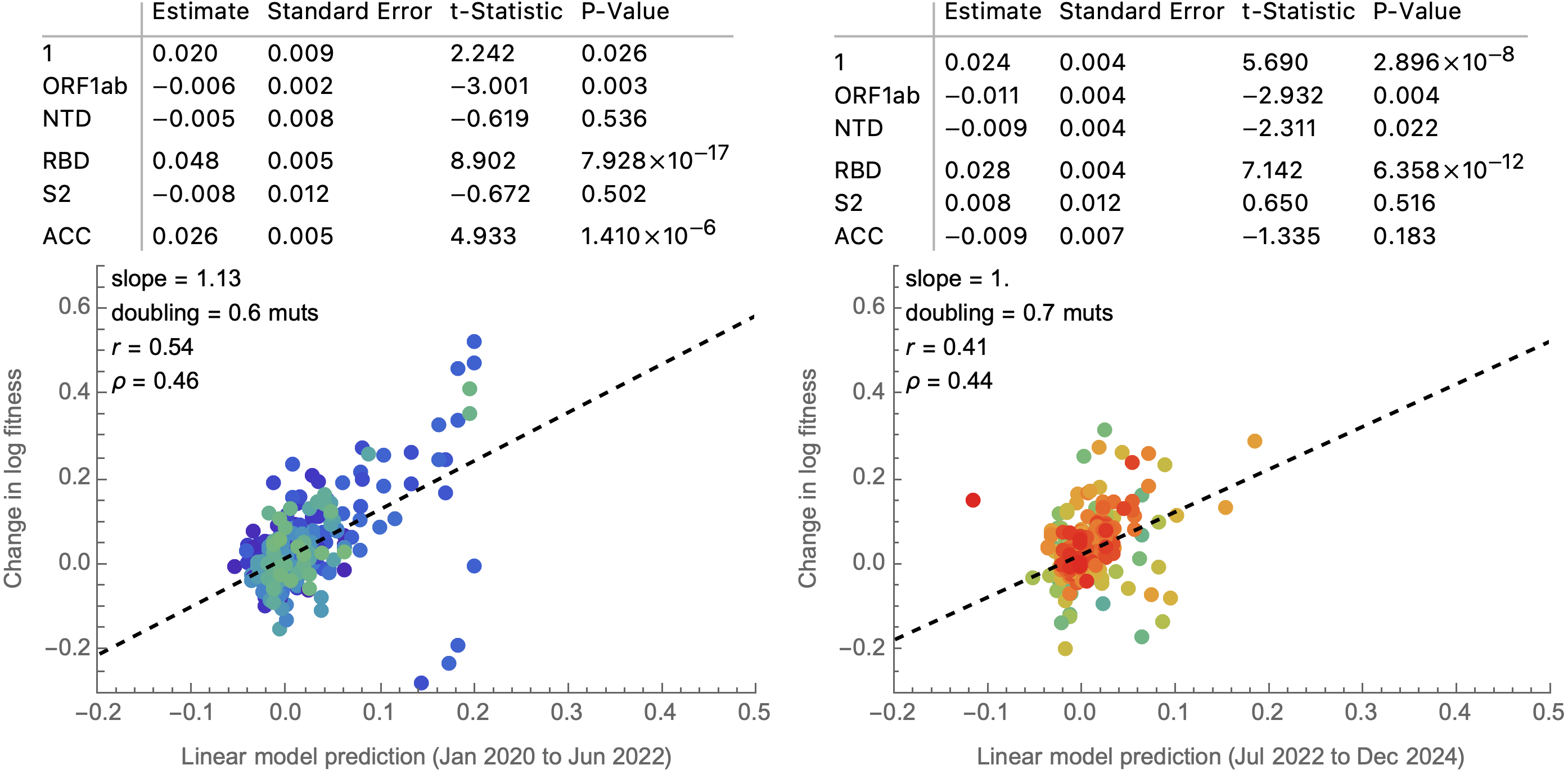
Ongoing work by Bloom Lab to conduct high-throughput experimental measurements of ACE2 binding and immune escape
Prediction of variant fitness from empirical priors
Rather than estimate variant specific fitness $f_i$ directly, instead parameterize the "innovation" in fitness in going from parent lineage $p$ to child lineage $i$ as $\delta_i = (f_i - f_p)$.
Compare a non-informative model of $$\delta_i = (f_i - f_p) \sim \mathrm{Normal}(0, \sigma)$$ to a model where each "innovation" value has an informed prior based on a linear combination of predictors such as ACE2 binding, immune escape and spike mutations, where $z_k$ represents the value of predictor $k$ $$\delta_i = (f_i - f_p) \sim \mathrm{Normal}\left(\sum_k \beta_k \, z_k, \sigma\right)$$
Figgins et al. In prep.
Still need approaches that explicitly model mutations and emergence of novel lineages
Acknowledgements
Seasonal influenza and SARS-CoV-2 genomics: Data producers from all over the world, GISAID
Nextstrain: Richard Neher, Ivan Aksamentov, John SJ Anderson, Kim Andrews, Jennifer Chang, James Hadfield, Emma Hodcroft, John Huddleston, Jover Lee, Victor Lin, Cornelius Roemer, Thomas Sibley
MLR and fitness modeling: Marlin Figgins, Eslam Abousamra, Jover Lee, James Hadfield, John Huddleston, Philippa Steinberg, Jesse Bloom, Cornelius Roemer, Richard Neher
Bedford Lab:
John Huddleston,
James Hadfield,
Katie Kistler,
Thomas Sibley,
Jover Lee,
Miguel Paredes,
Marlin Figgins,
Victor Lin,
Jennifer Chang,
Nashwa Ahmed,
Cécile Tran Kiem,
Kim Andrews,
Cristian Ovaduic,
Philippa Steinberg,
Jacob Dodds,
John SJ Anderson
Nobuaki Masaki
Amin Bemanian
