Fitness flux in SARS-CoV-2 and seasonal influenza H3N2
Trevor Bedford
Fred Hutchinson Cancer Center / Howard Hughes Medical Institute
25 Apr 2025
Infectious Disease and Microbiome Program Seminar
Broad Institute of MIT and Harvard
Slides at: bedford.io/talks
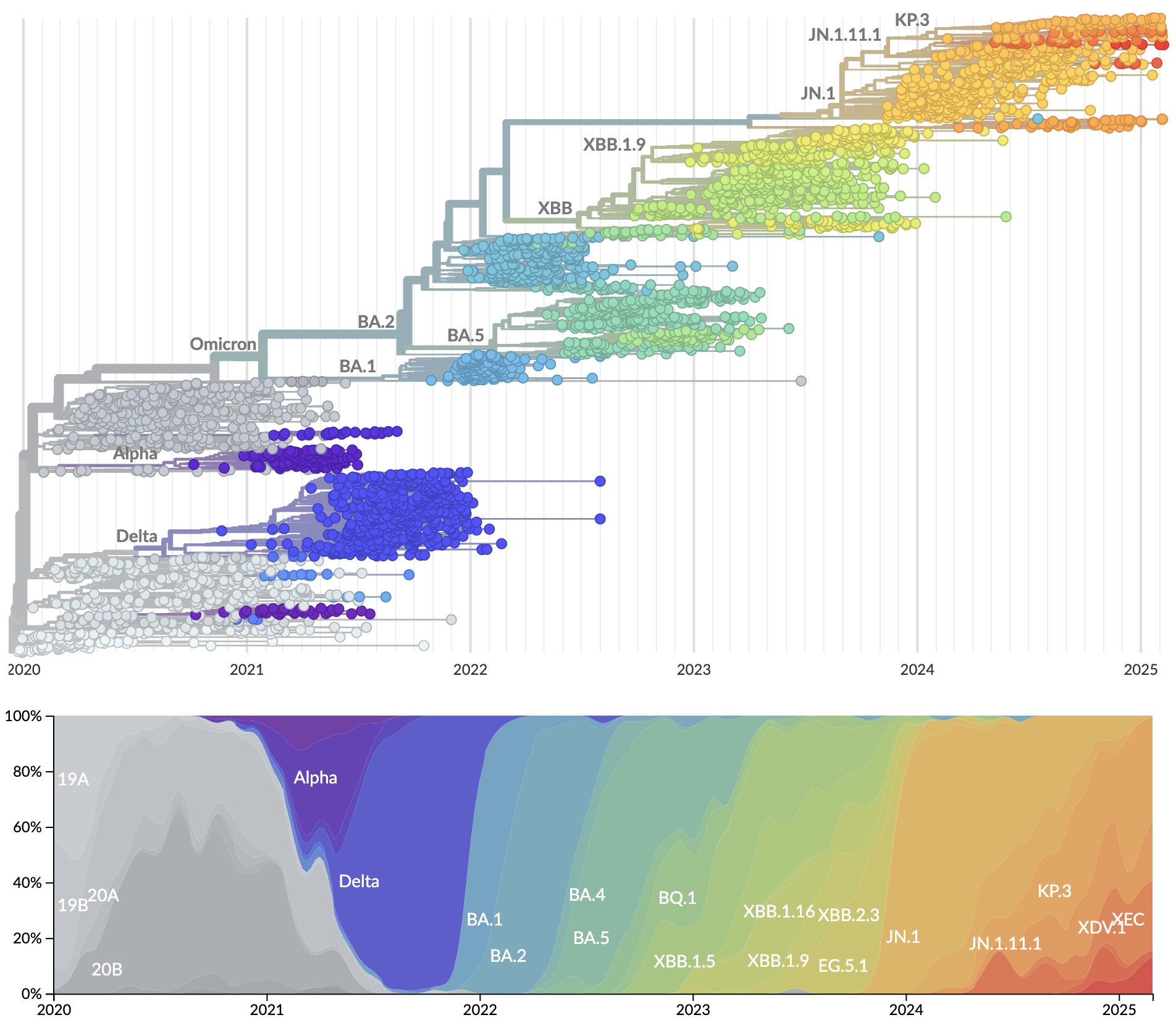
Genetic relationships of globally sampled SARS-CoV-2 from 2020 to present
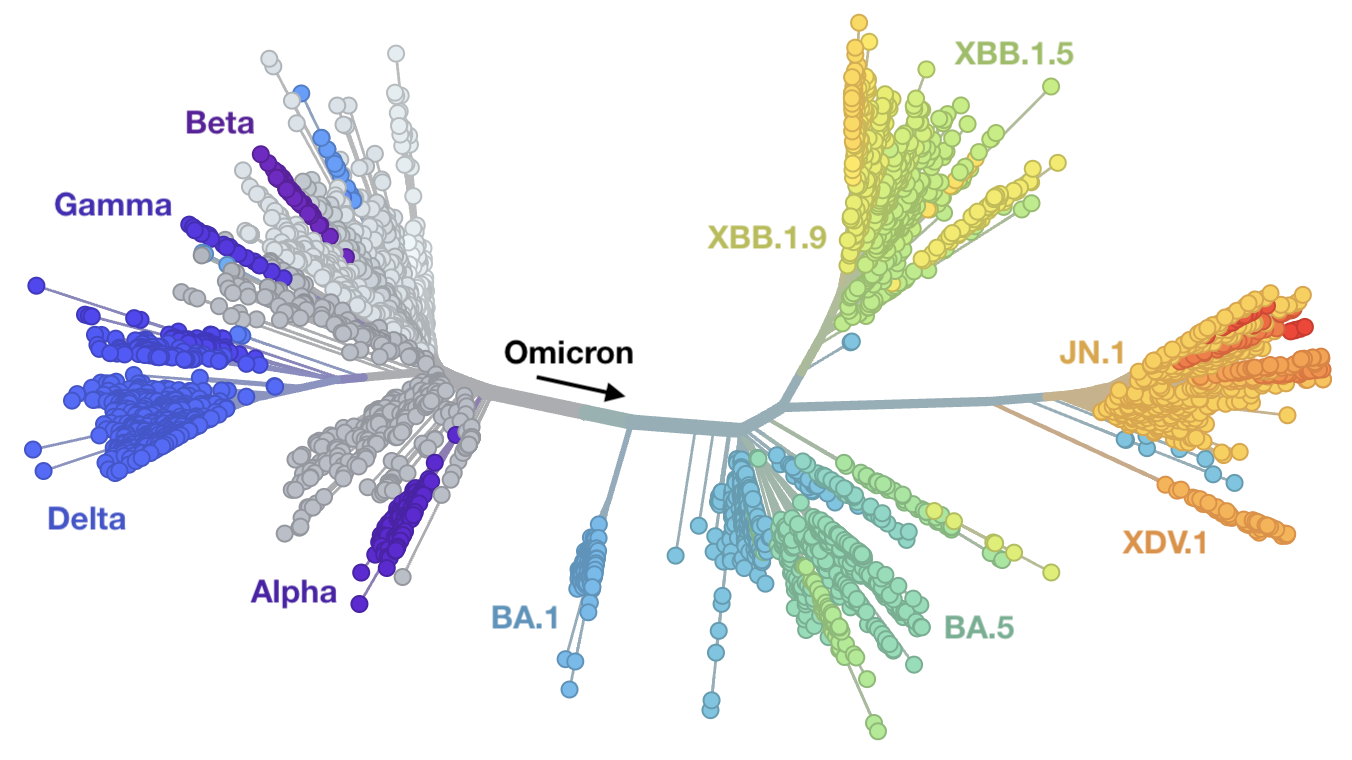
Rapid displacement of existing diversity by emerging variants
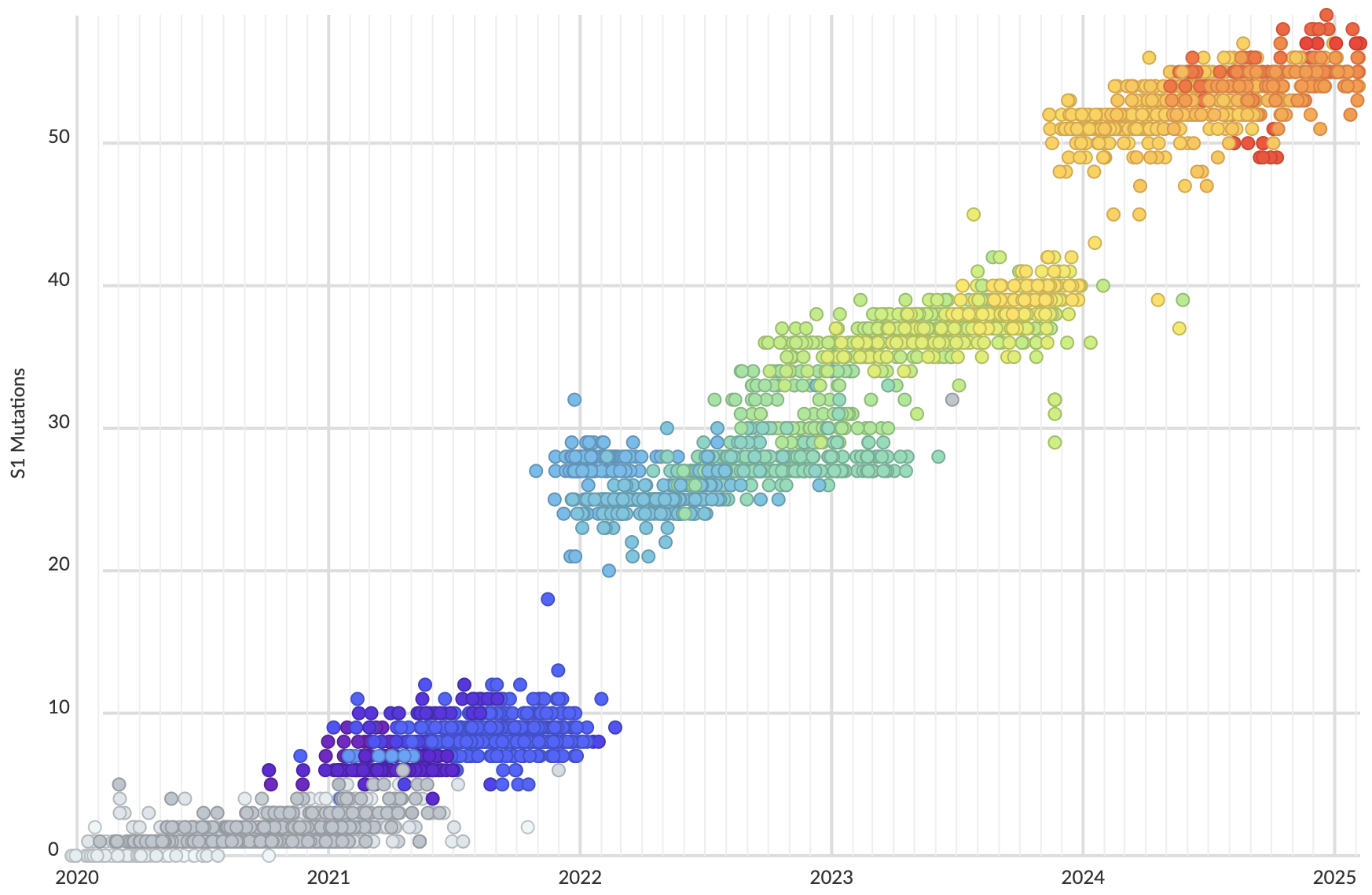
Mutations in S1 domain of spike protein driving displacement
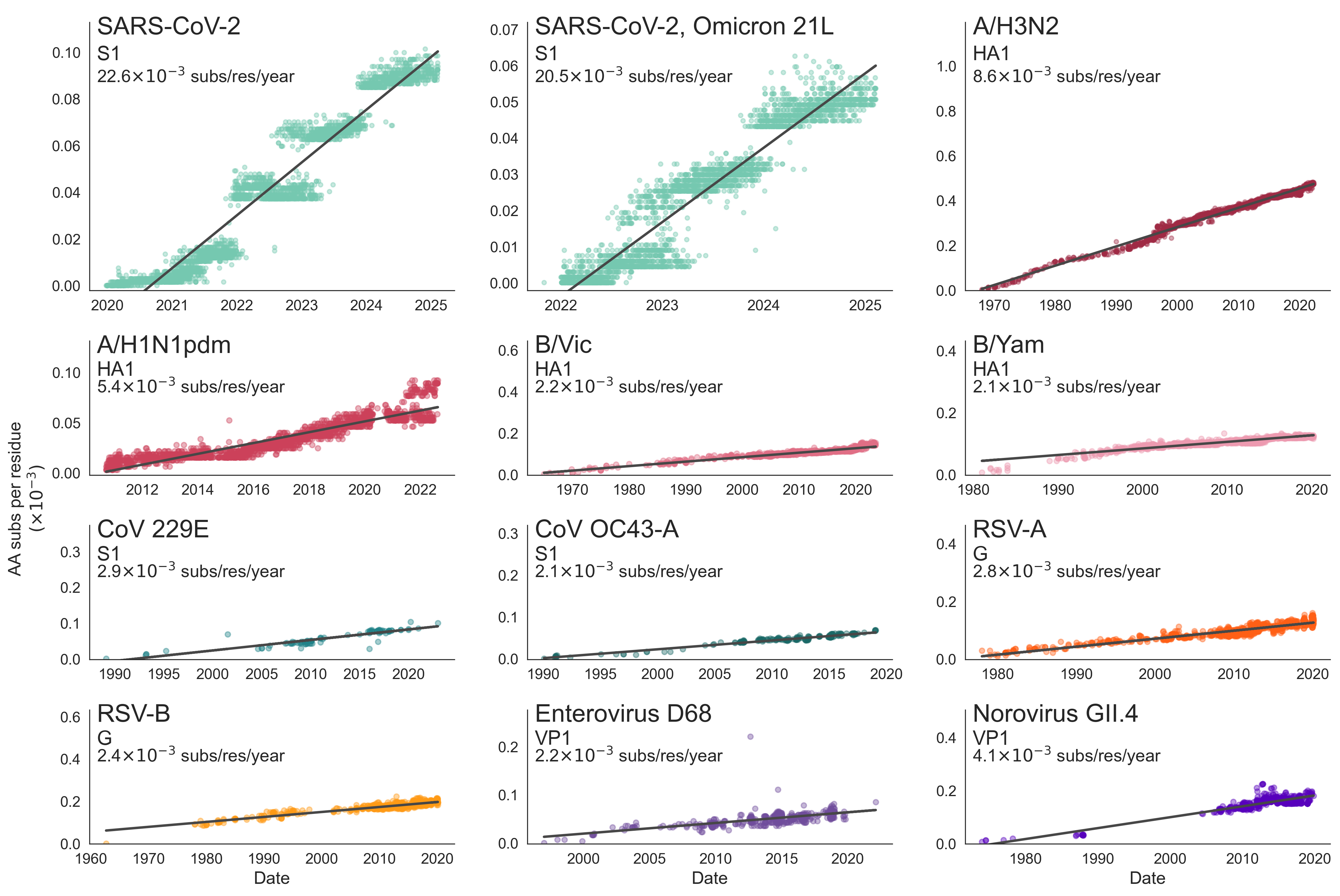
SARS-CoV-2 evolution fast relative to previous endemic viruses
This talk
- Frequency dynamics and fitness estimation
- Evolutionary forecasting
- Fitness flux
- Mutational fitness effects
Frequency dynamics and fitness estimation
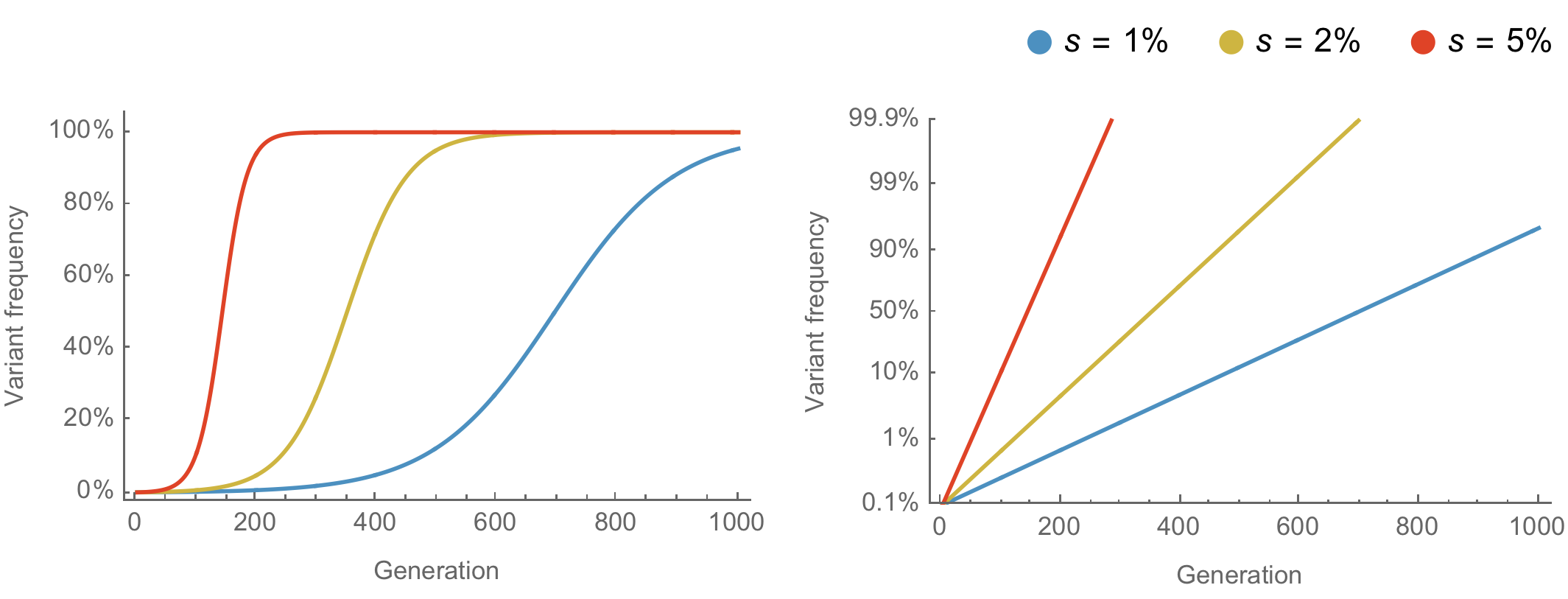
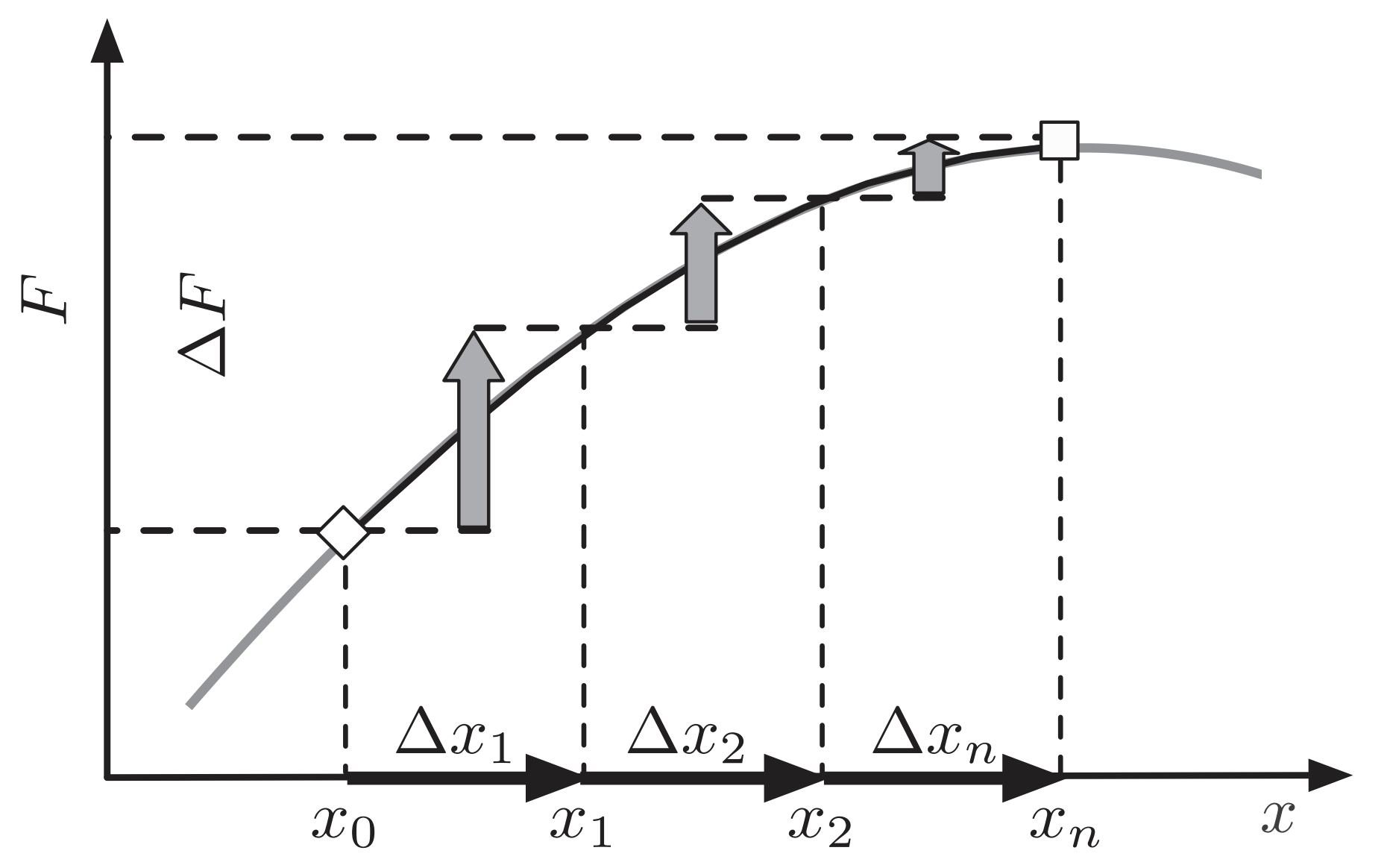
Population genetic expectation of variant frequency under selection
$x' = \frac{x \, (1+s)}{x \, (1+s) + (1-x)}$ for frequency $x$ over one generation with selective advantage $s$
$x(t) = \frac{x_0 \, (1+s)^t}{x_0 \, (1+s)^t + (1-x_0)}$ for initial frequency $x_0$ over $t$ generations
Trajectories are linear once logit transformed via $\mathrm{log}(\frac{x}{1 - x})$
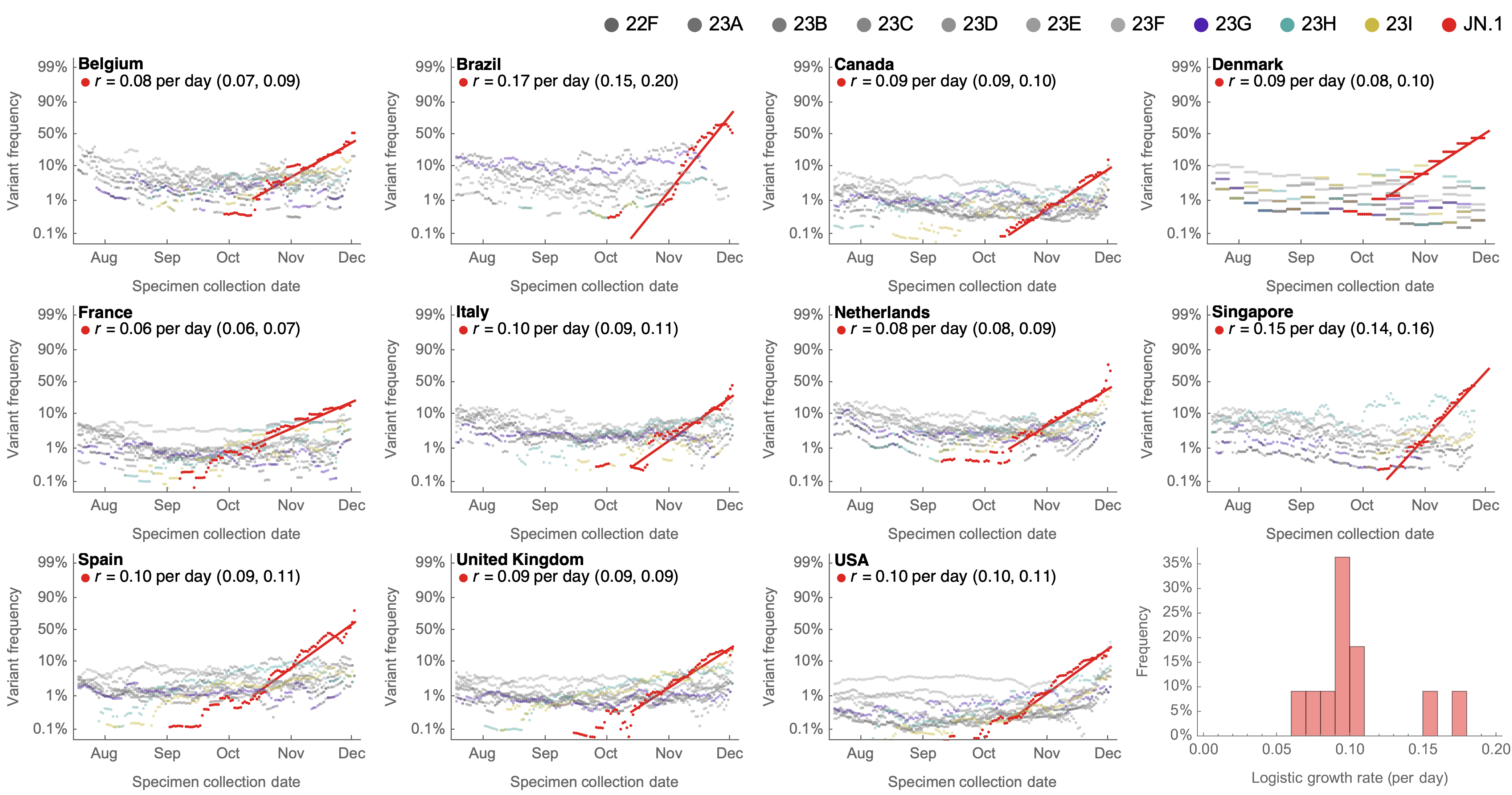
Consistent frequency dynamics in logit space (BA.2 Mar 2022)
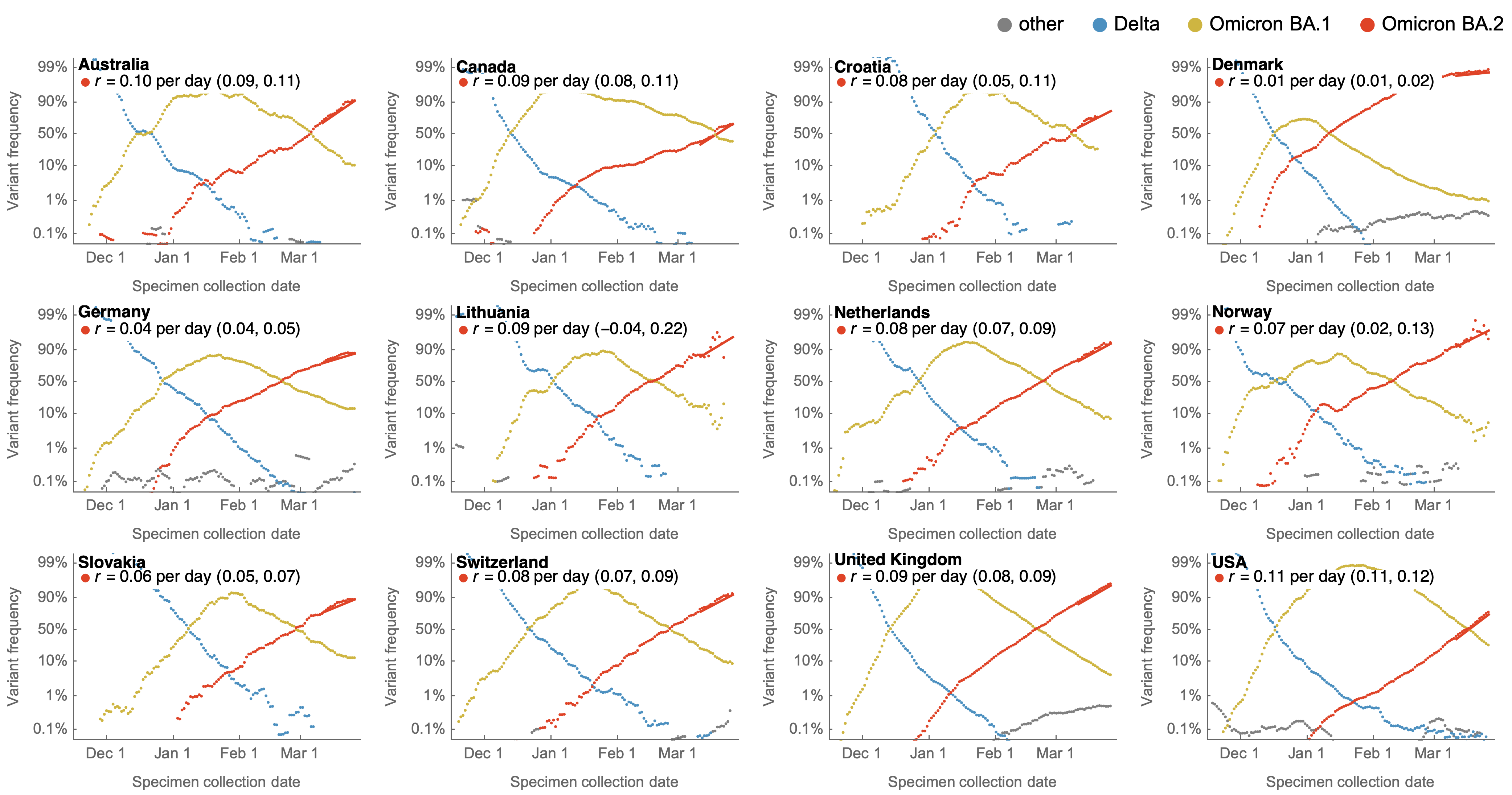
Consistent frequency dynamics in logit space (JN.1 Dec 2023)
Multinomial logistic regression
Multinomial logistic regression across $n$ variants models the probability of a virus sampled at time $t$ belonging to variant $i$ as equal to its frequency $x_i(t)$
$$\mathrm{Pr}(X = i) = x_i(t) = \frac{p_i \, \mathrm{exp}(f_i \, t)}{\sum_j p_j \, \mathrm{exp}(f_j \, t) }$$
with $2n$ parameters consisting of $p_i$ the frequency of variant $i$ at initial timepoint
and $f_i$ the growth rate or fitness of variant $i$.
Various flavors of MLR implemented in evofr package
location variant date sequences Japan 22B 2023-02-10 242 Japan 22B 2023-02-11 56 Japan 22B 2023-02-12 70 Japan 22E 2023-02-10 80 Japan 22E 2023-02-11 21 Japan 22E 2023-02-12 27 USA 22B 2023-02-10 41 USA 22B 2023-02-11 23 USA 22B 2023-02-12 23 USA 22E 2023-02-10 368 USA 22E 2023-02-11 236 USA 22E 2023-02-12 246 ...
Multinomial logistic regression fits variant frequencies well
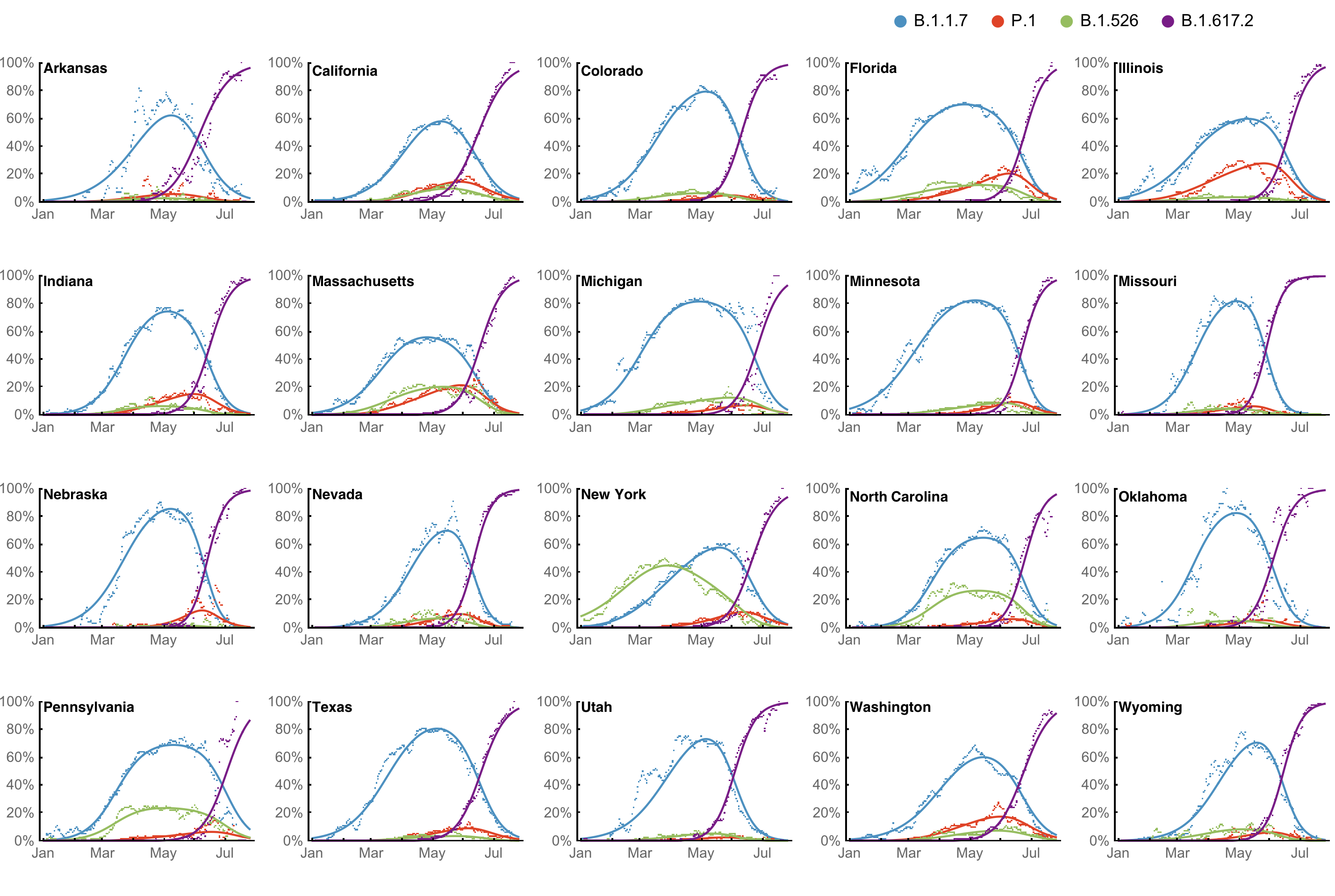
Original VOC viruses had substantially increased transmissibility
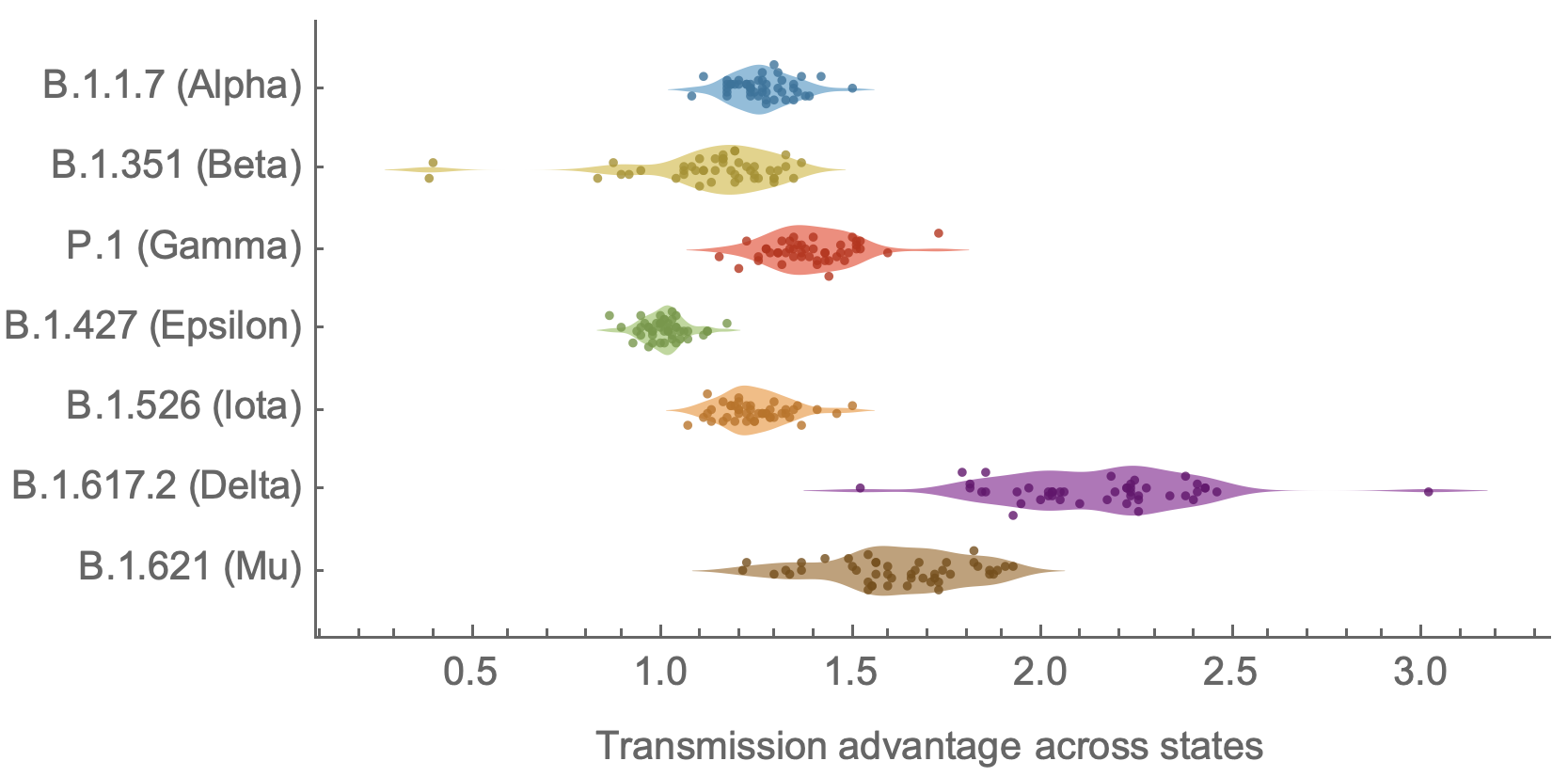
Evolutionary forecasting
Clade and lineage forecasts continuously updated at nextstrain.org
Rapid sweep of JN.1 over Dec to Jan 2024
Assessing MLR models for short-term frequency forecasting
Retrospective projections twice monthly during 2022
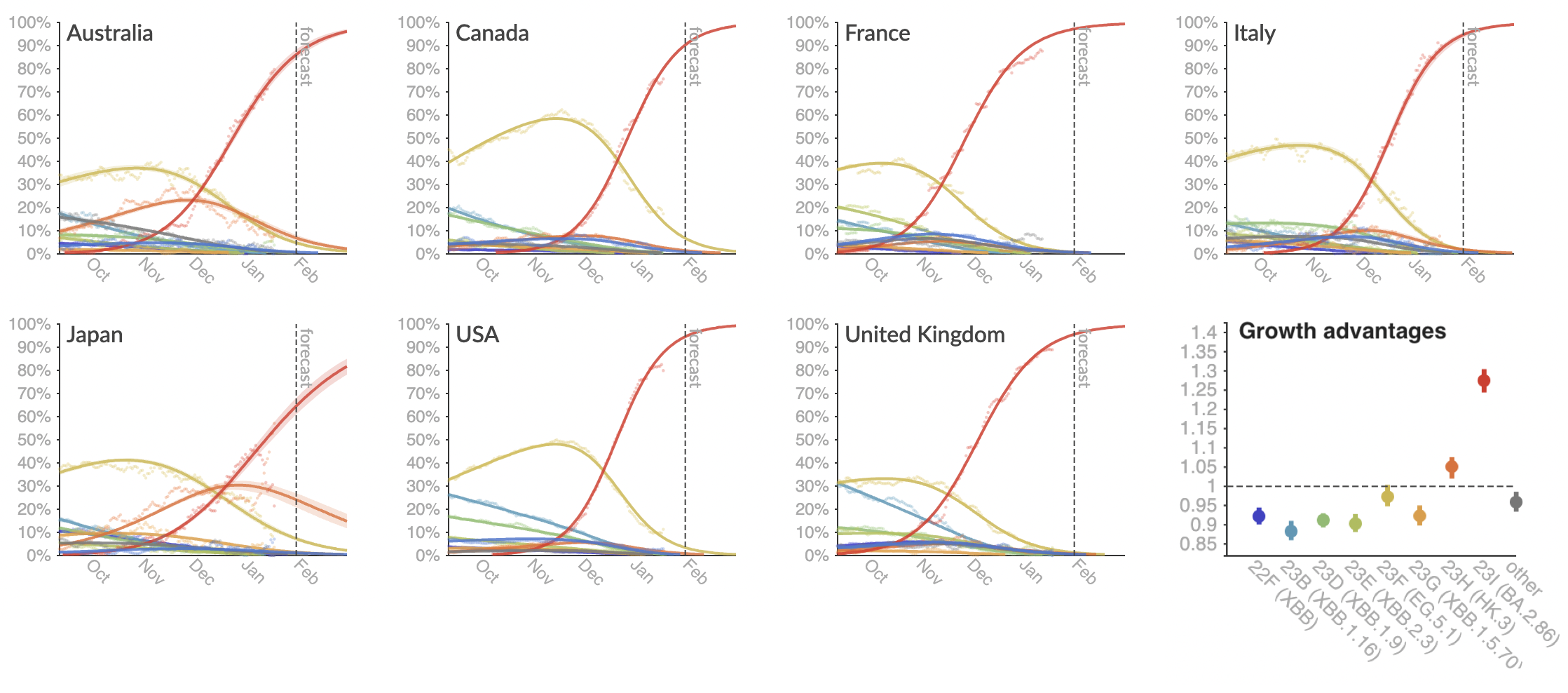
+30 day short-term forecasts across different countries
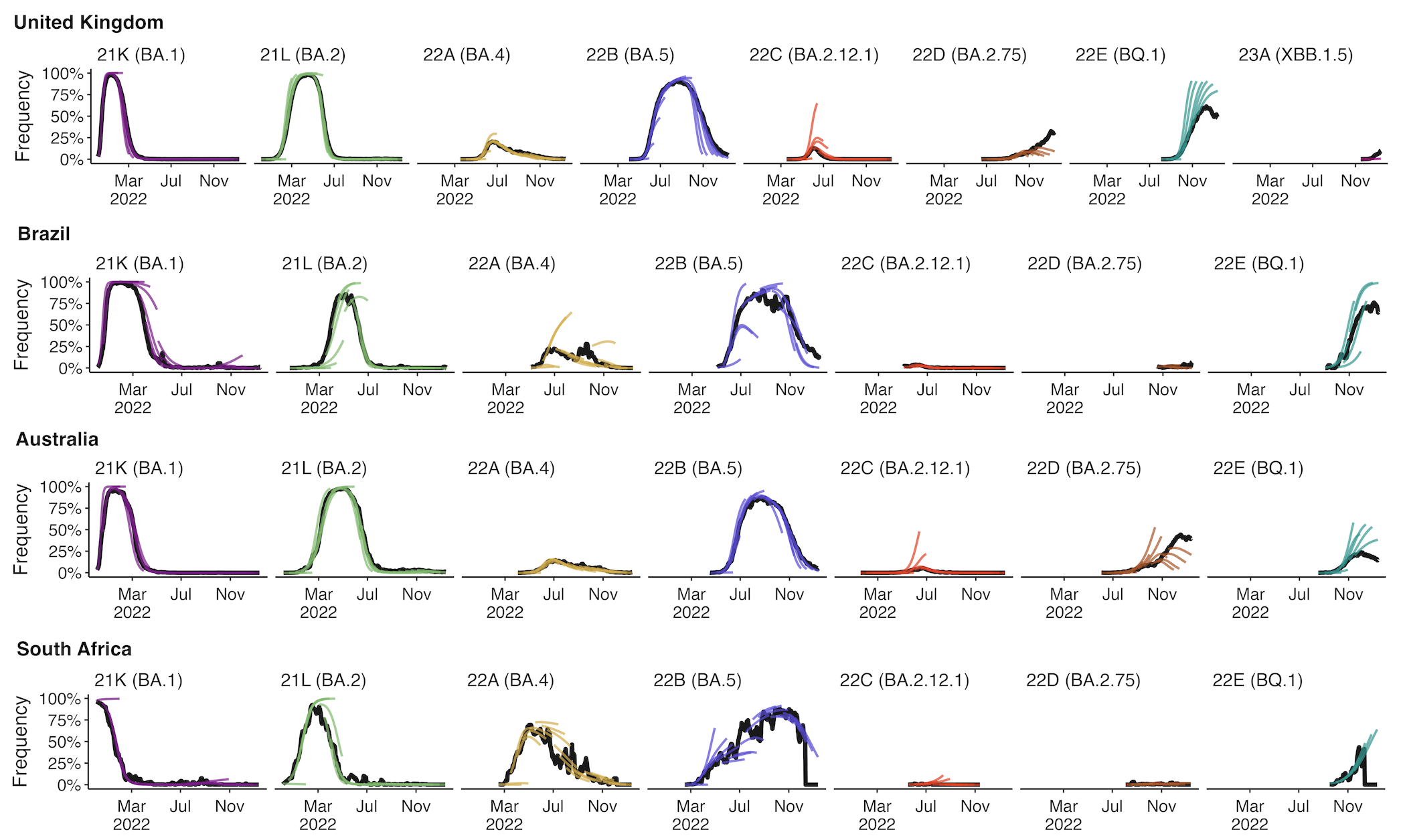
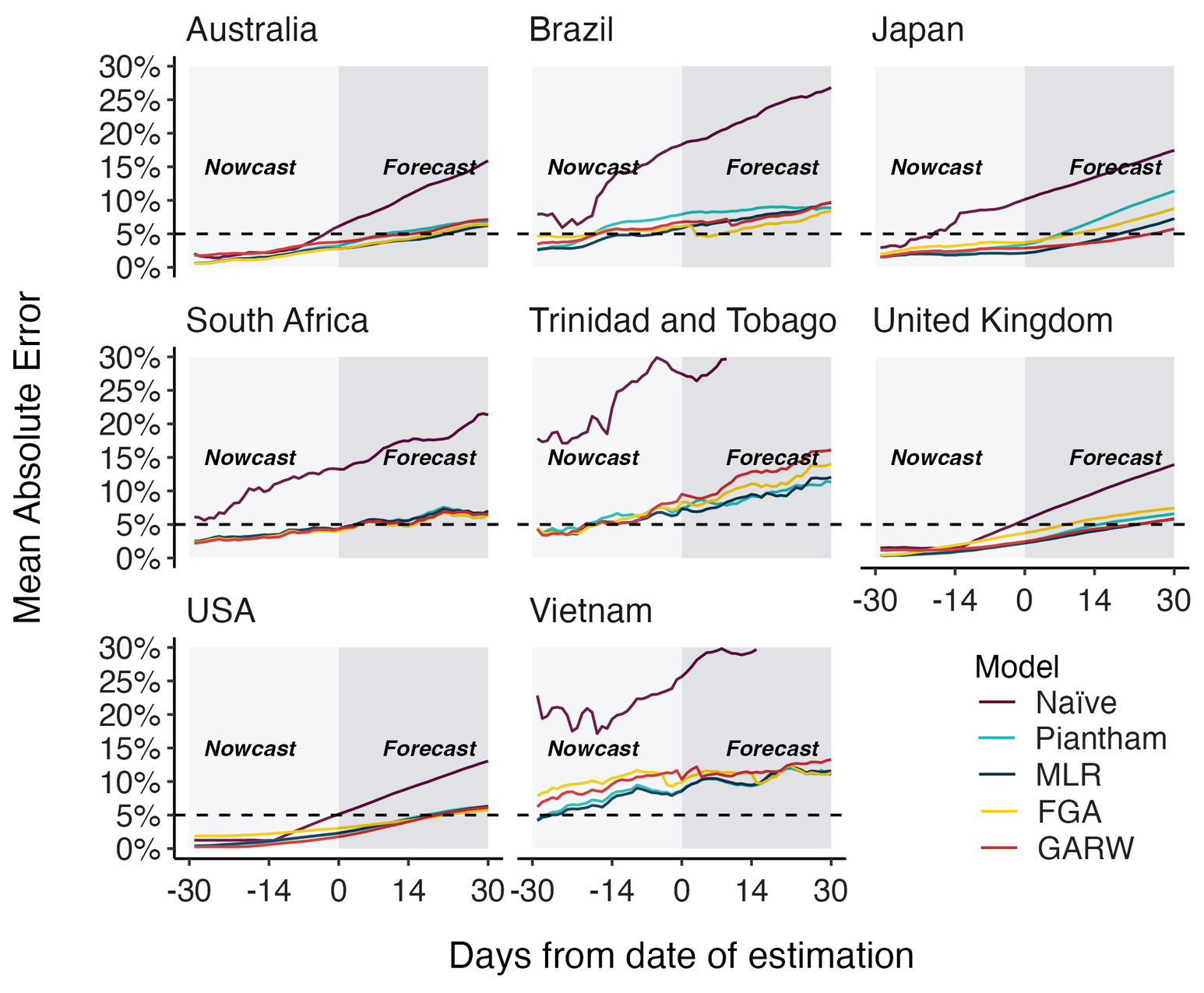
MLR models generate accurate short-term forecasts
30 days out, countries range from 5 to 15% mean absolute error
Correlates with data availability (median number of sequences available from the previous 30 days):
- USA
- ~45k sequences
- Australia
- ~4k sequences
- South Africa
- 170 sequences
- Vietnam
- 30 sequences
Fitness flux
Fitness flux is the rate of change of fitness across the population
With variant frequency $x_i(t)$ and constant variant fitness $f_i$,
fitness flux equals the rate of change of mean population fitness
Mean population fitness $\bar{f}(t) = \sum_i x_i(t) \, f_i$ Fitness flux $\phi(t) = \Delta \bar{f}(t) / \Delta t$
Defining terms
| Mean population fitness | $\bar{f}(t) = \sum_i x_i(t) \, f_i$ |
| Variance in fitness across population | $\mathrm{Var}[f(t)] = \sum_i x_i(t) \, (f_i - \bar{f}(t))^2$ |
| Velocity of mean population fitness | $\psi(t) = \Delta \bar{f}(t) / \Delta t$ |
| Fitness flux | $\phi(t) = \left( \sum_i \Delta x_i \, f_i \right) / \Delta t$ |
Clade-level frequency dynamics and MLR fits in sliding windows
Constant clade fitness within each window, USA data only, ignores within-clade fitness variation
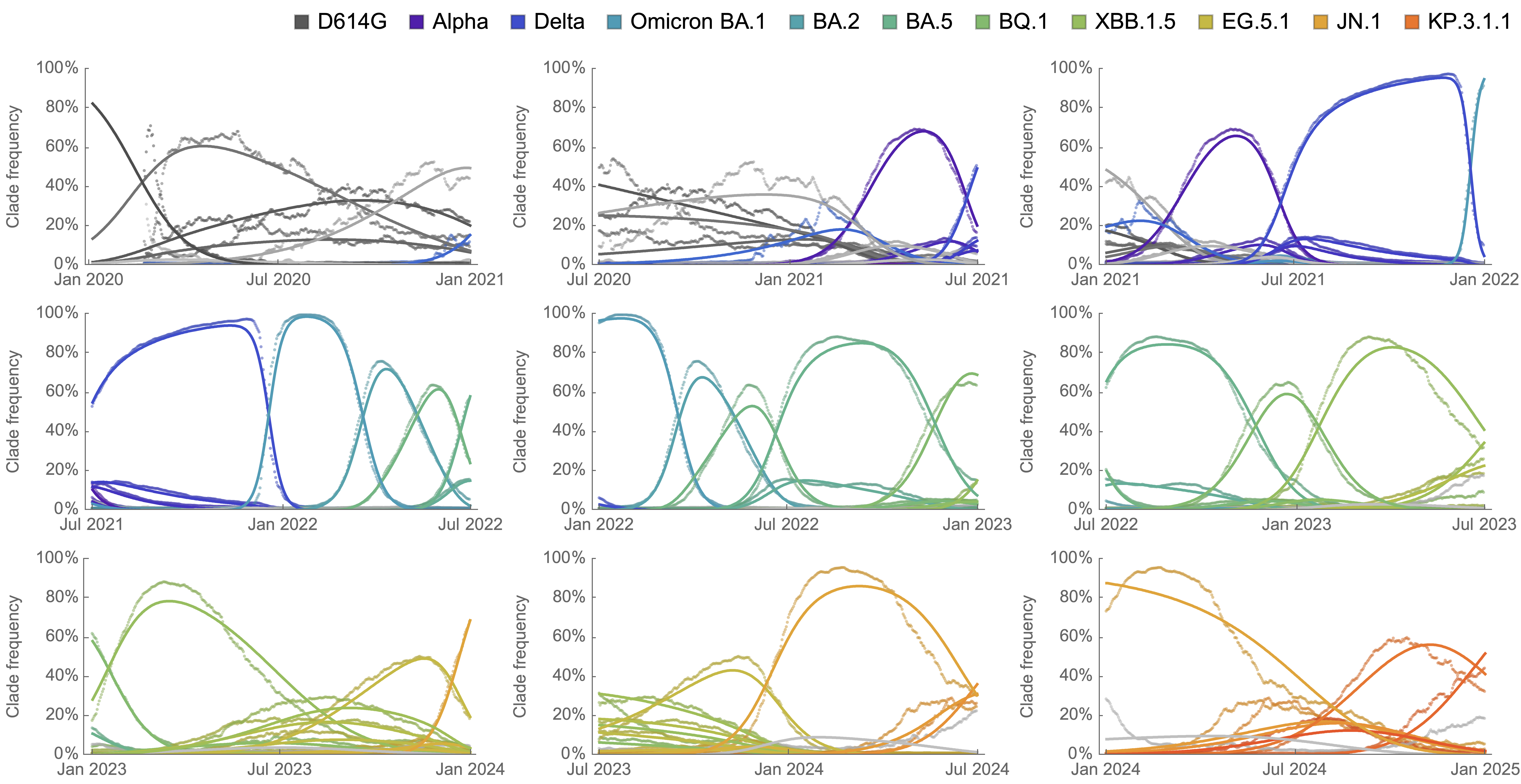
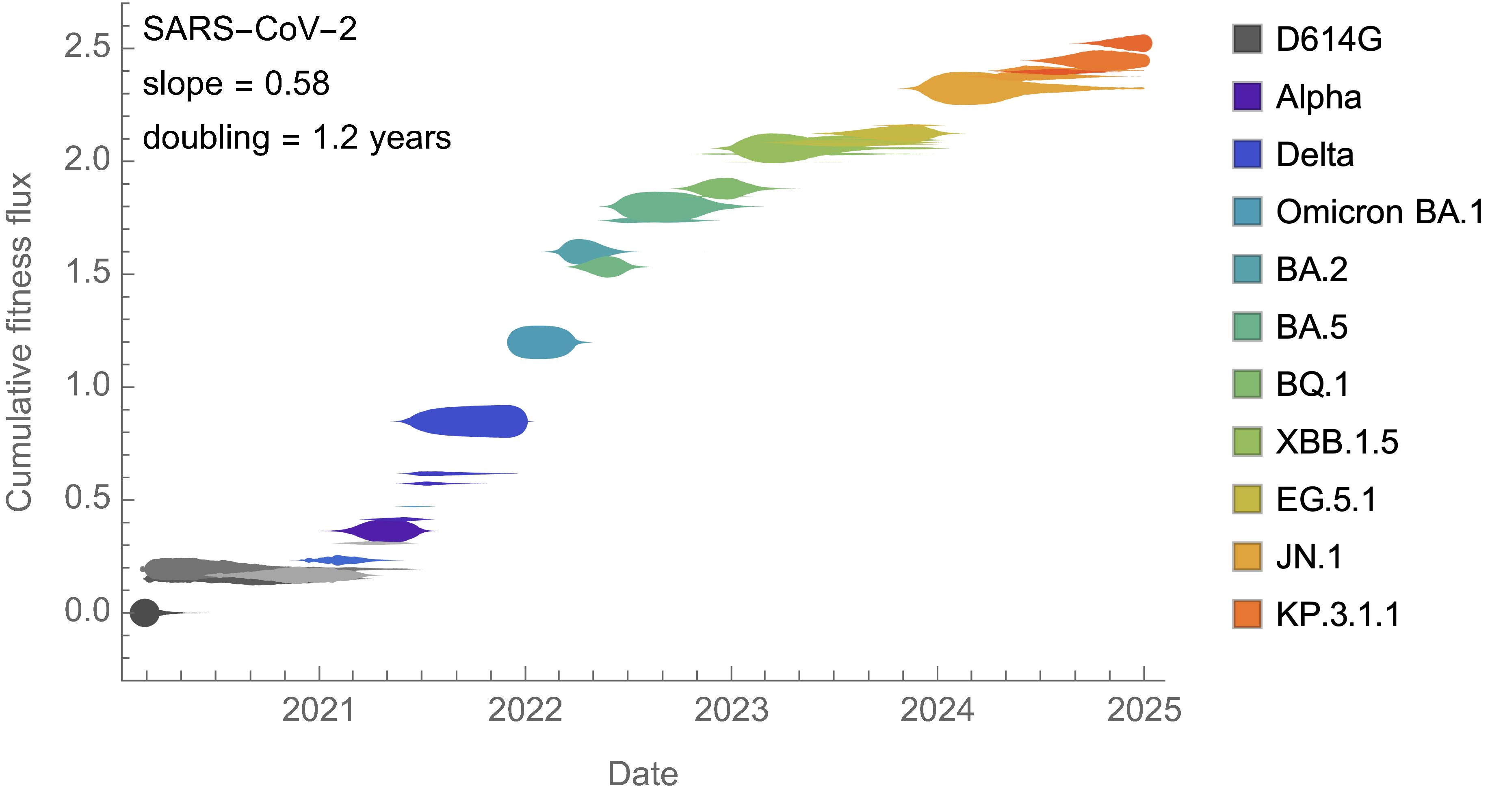
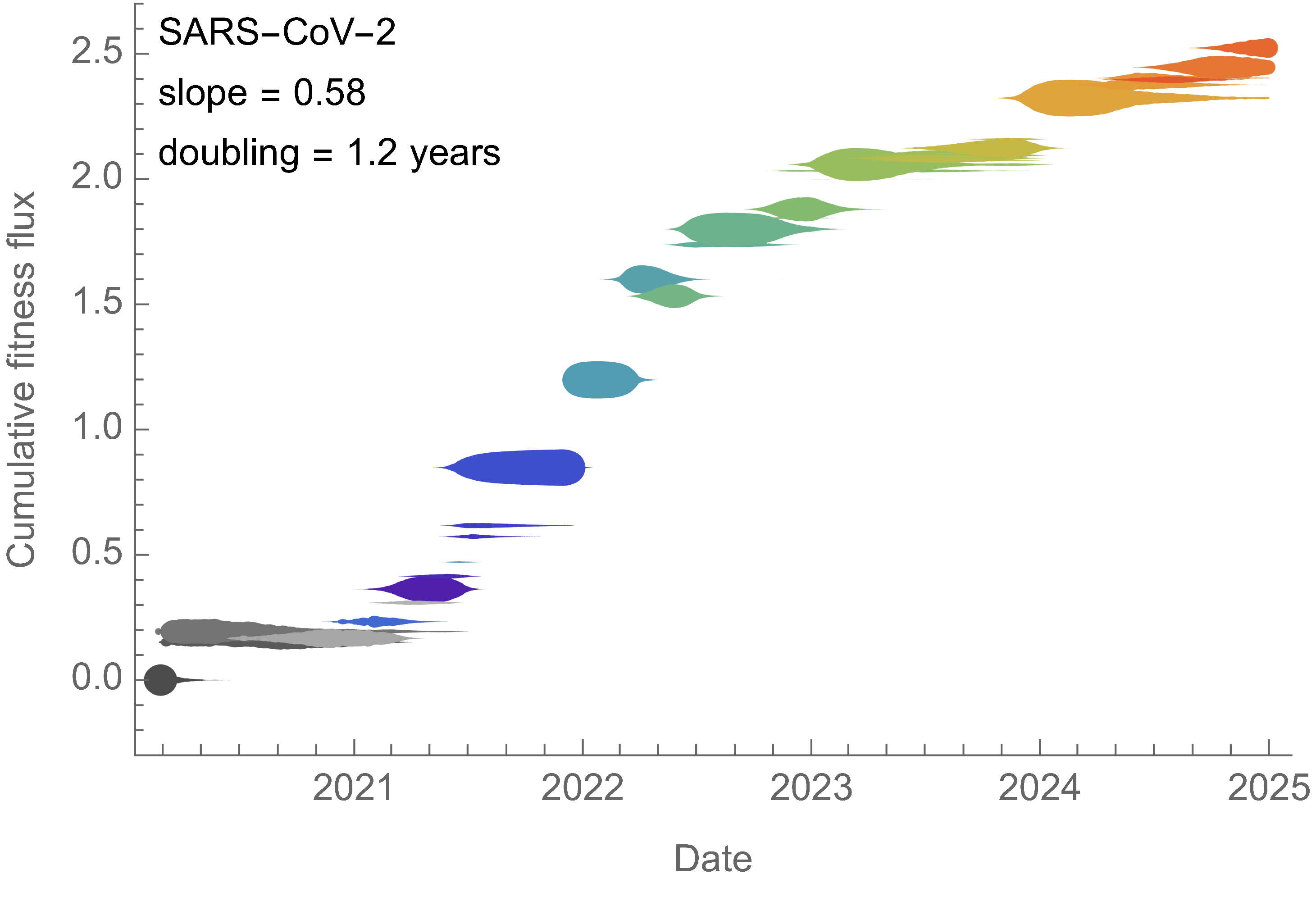
SARS-CoV-2 roughly doubled in fitness every year
Line thickness is proportional to variant frequency, 36 total variants
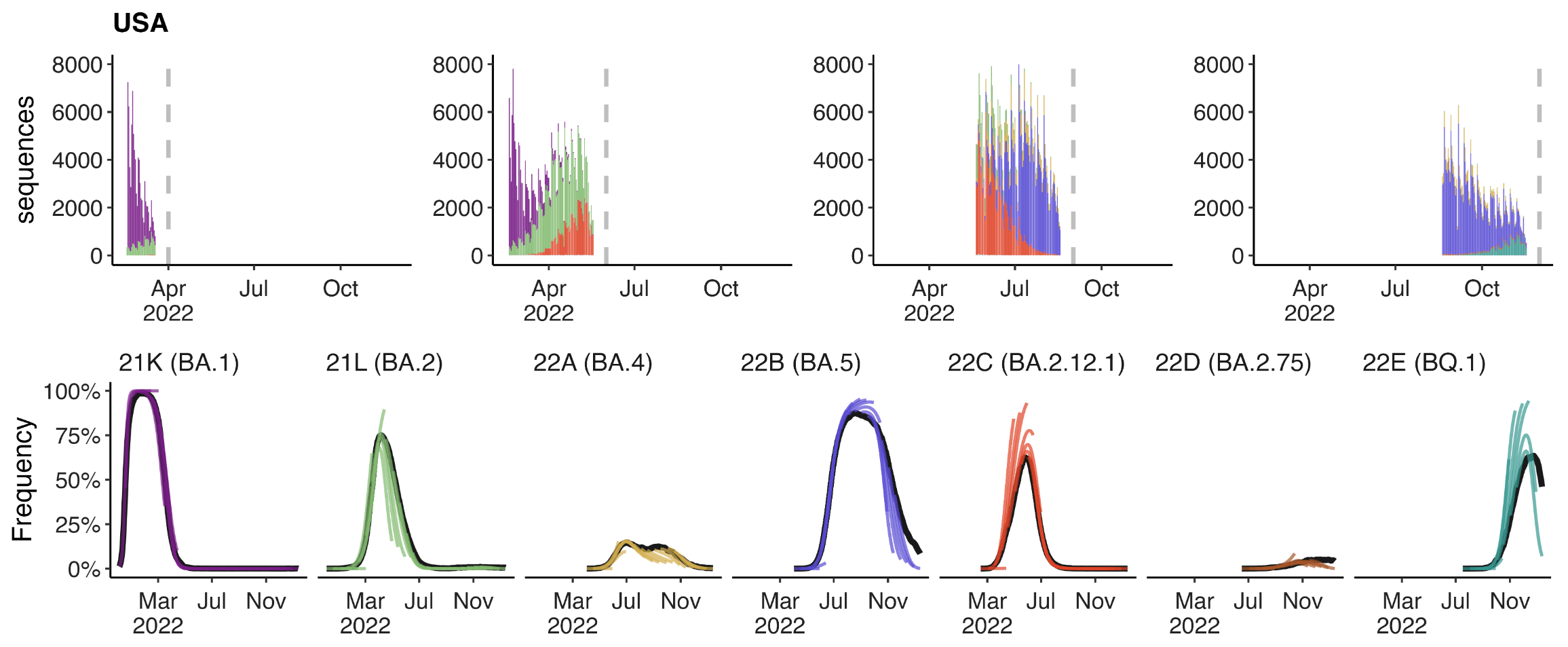
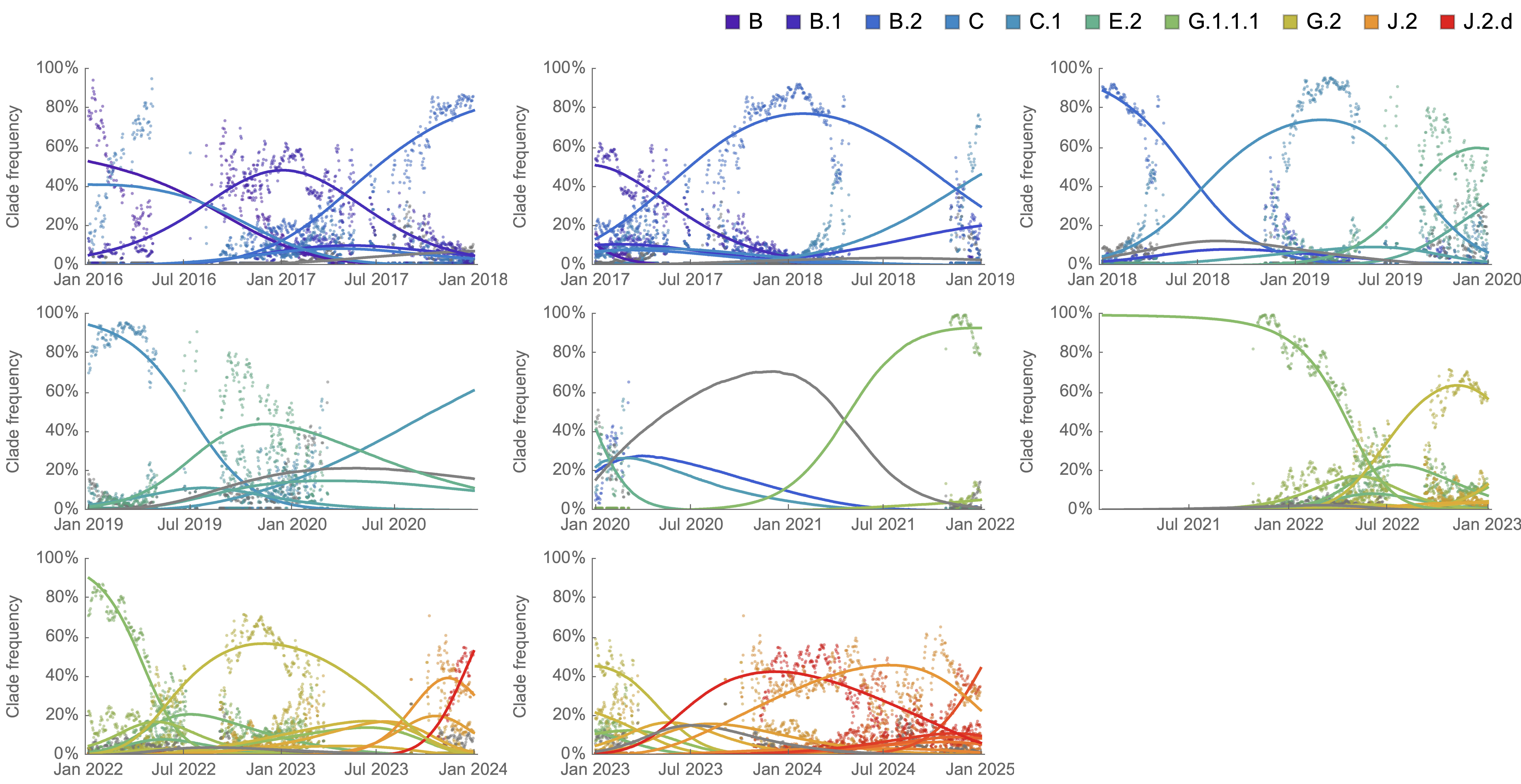
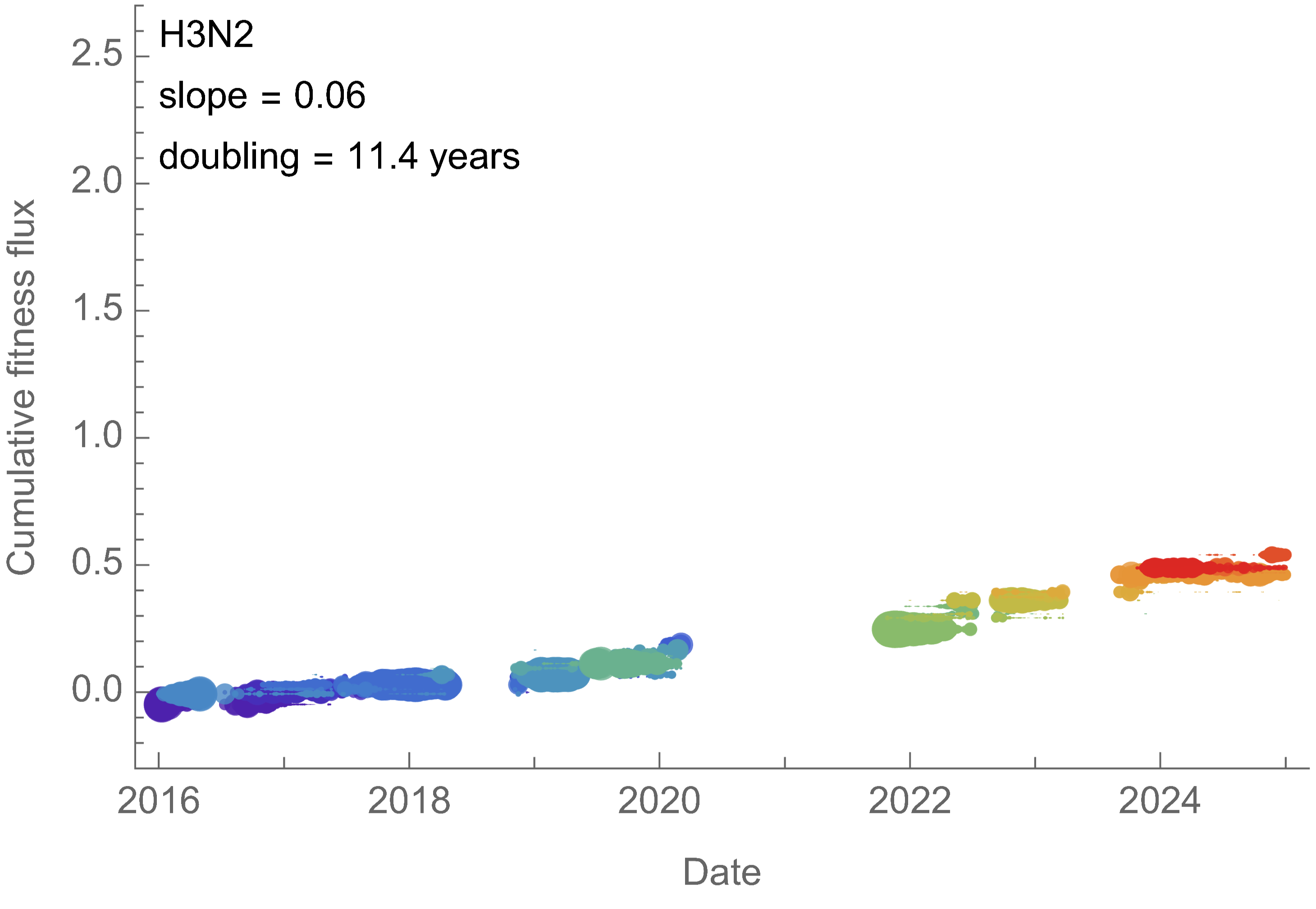
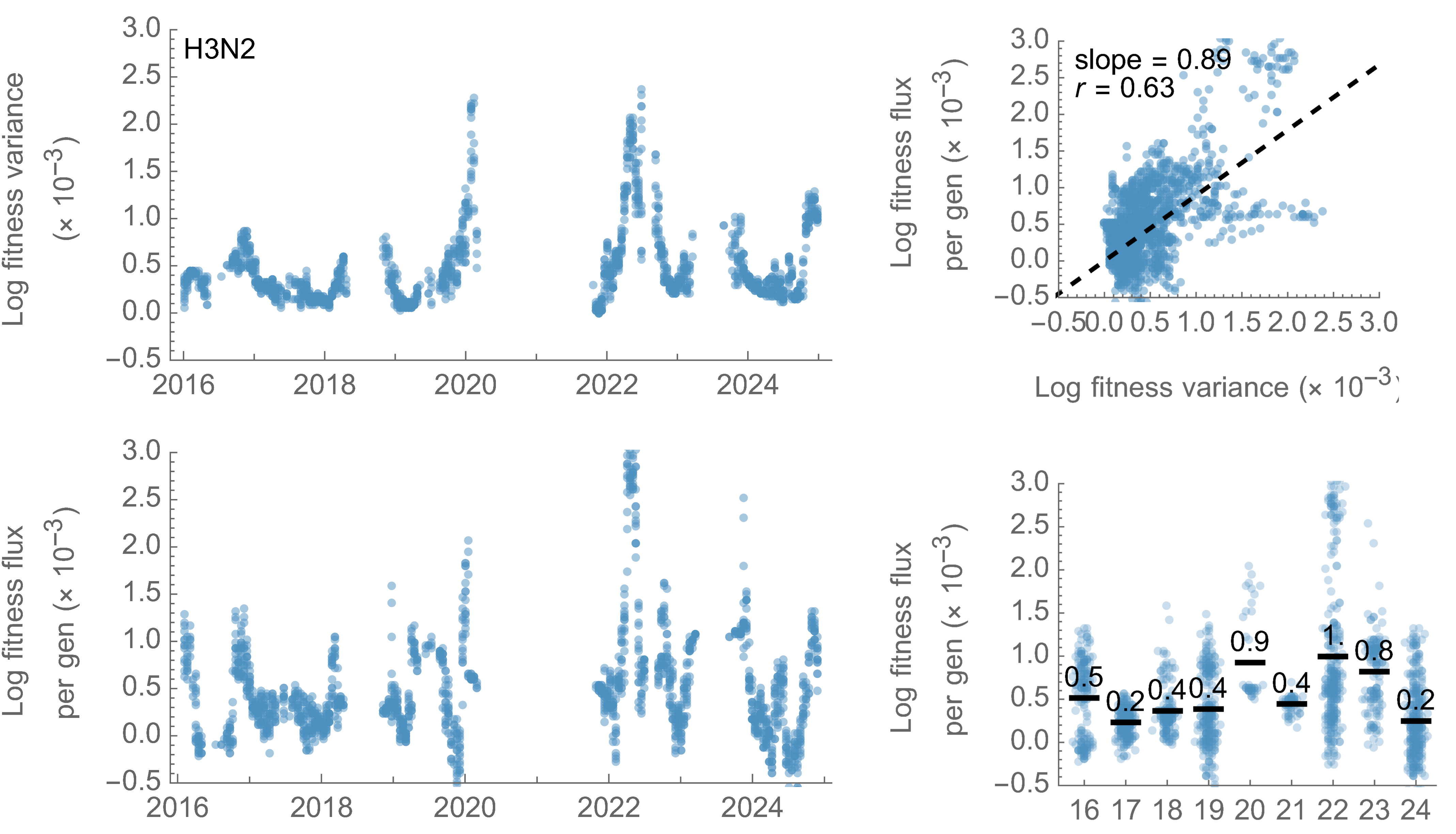
Analogous frequency dynamics and MLR fits for H3N2
Constant clade fitness within each window, USA data only, ignores within-clade fitness variation
H3N2 roughly doubled in fitness every 10 years
Line thickness is proportional to variant frequency, 32 total variants
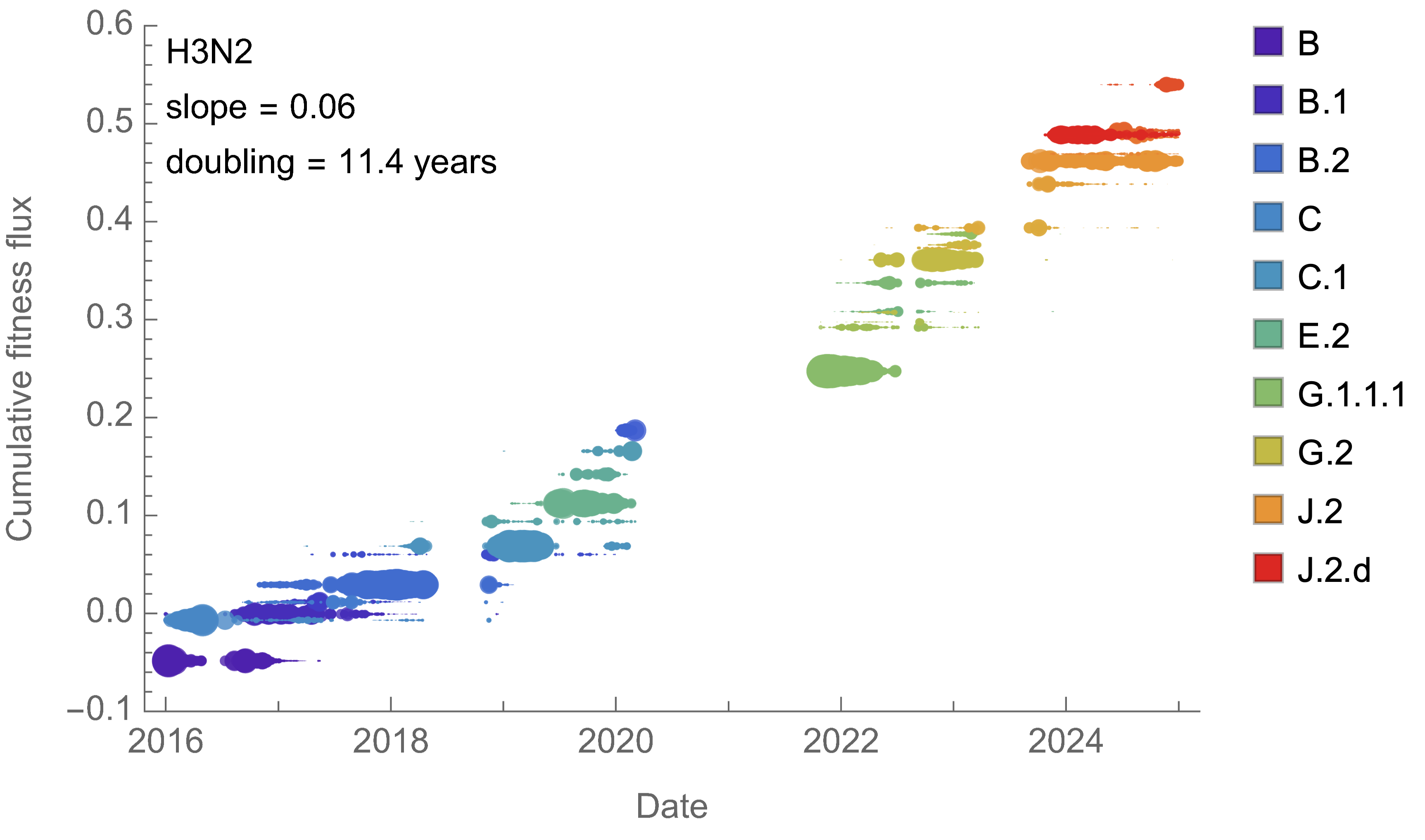
Dramatically faster fitness flux of SARS-CoV-2
Traveling fitness waves
Multistrain models produce traveling waves in antigenic space
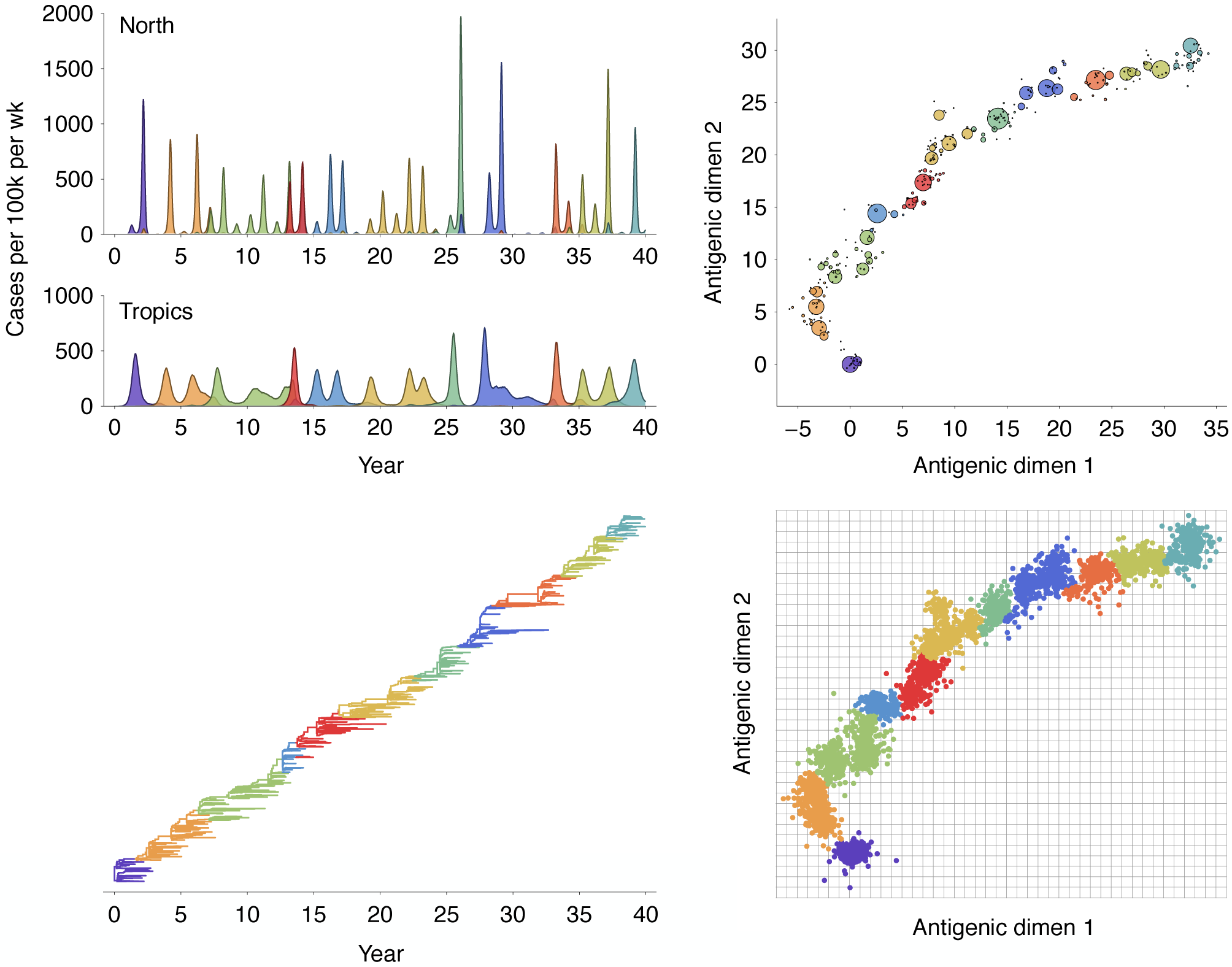
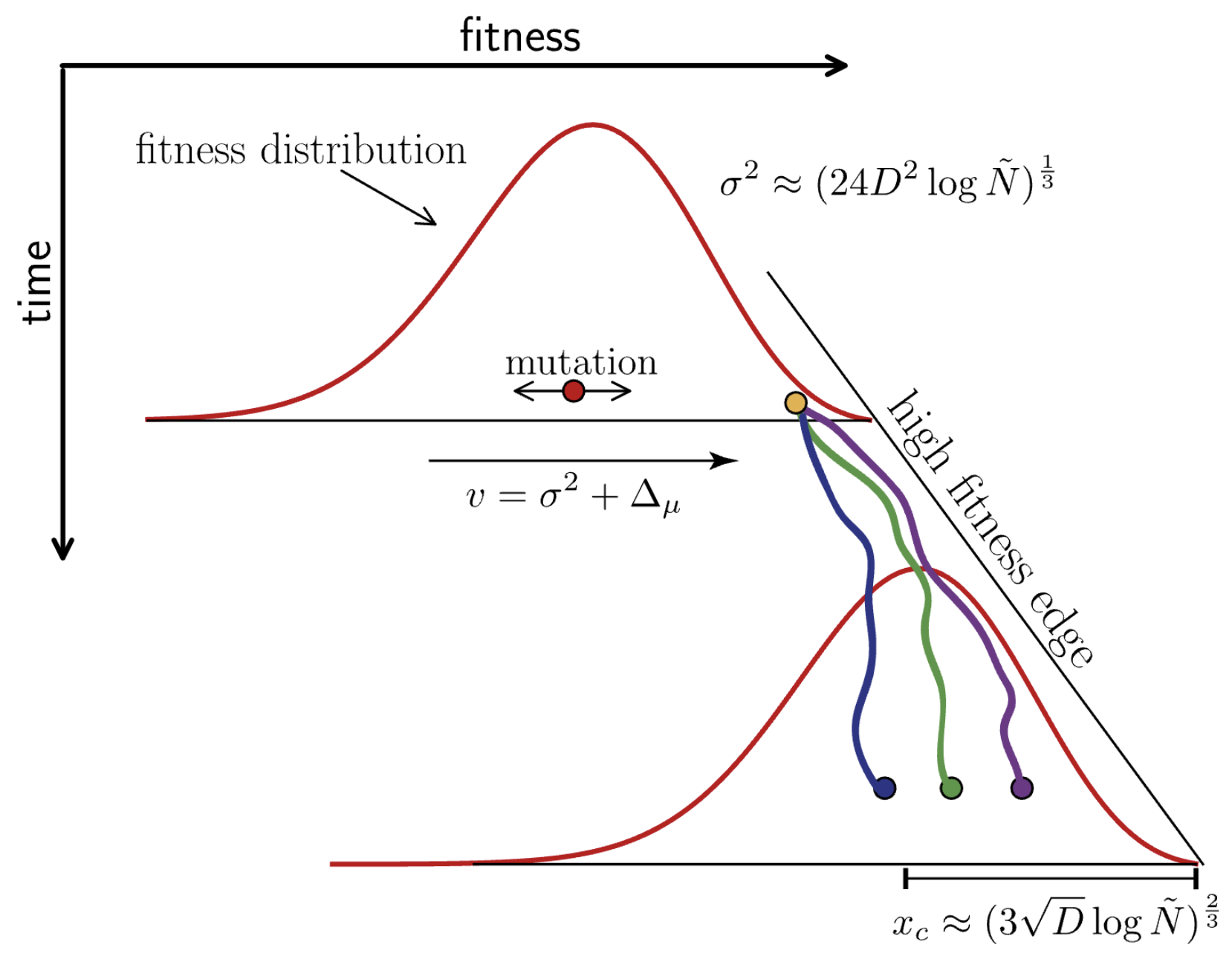
Many mutations of small effect create traveling fitness waves
Richard Neher and others have analytically characterized these waves
Diffusion constant $D = \mu \, \langle \delta^2 \rangle/2$, where the average $\langle \ldots \rangle$ is over the distribution of mutational effects $K(\delta)$
Using empirical frequencies and MLR fitness to characterize fitness wave
SARS-CoV-2
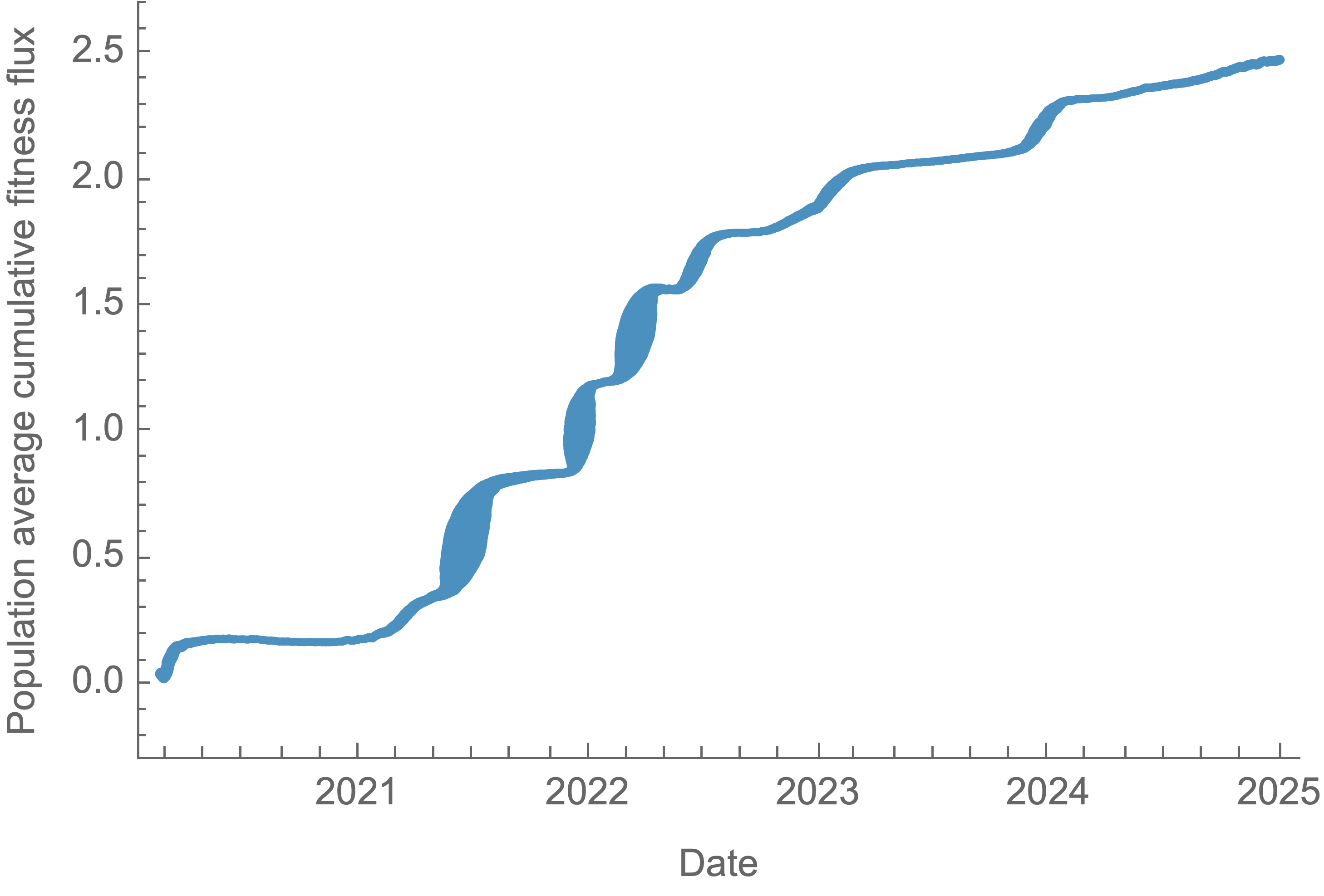
Fitness variance correlates well with fitness flux
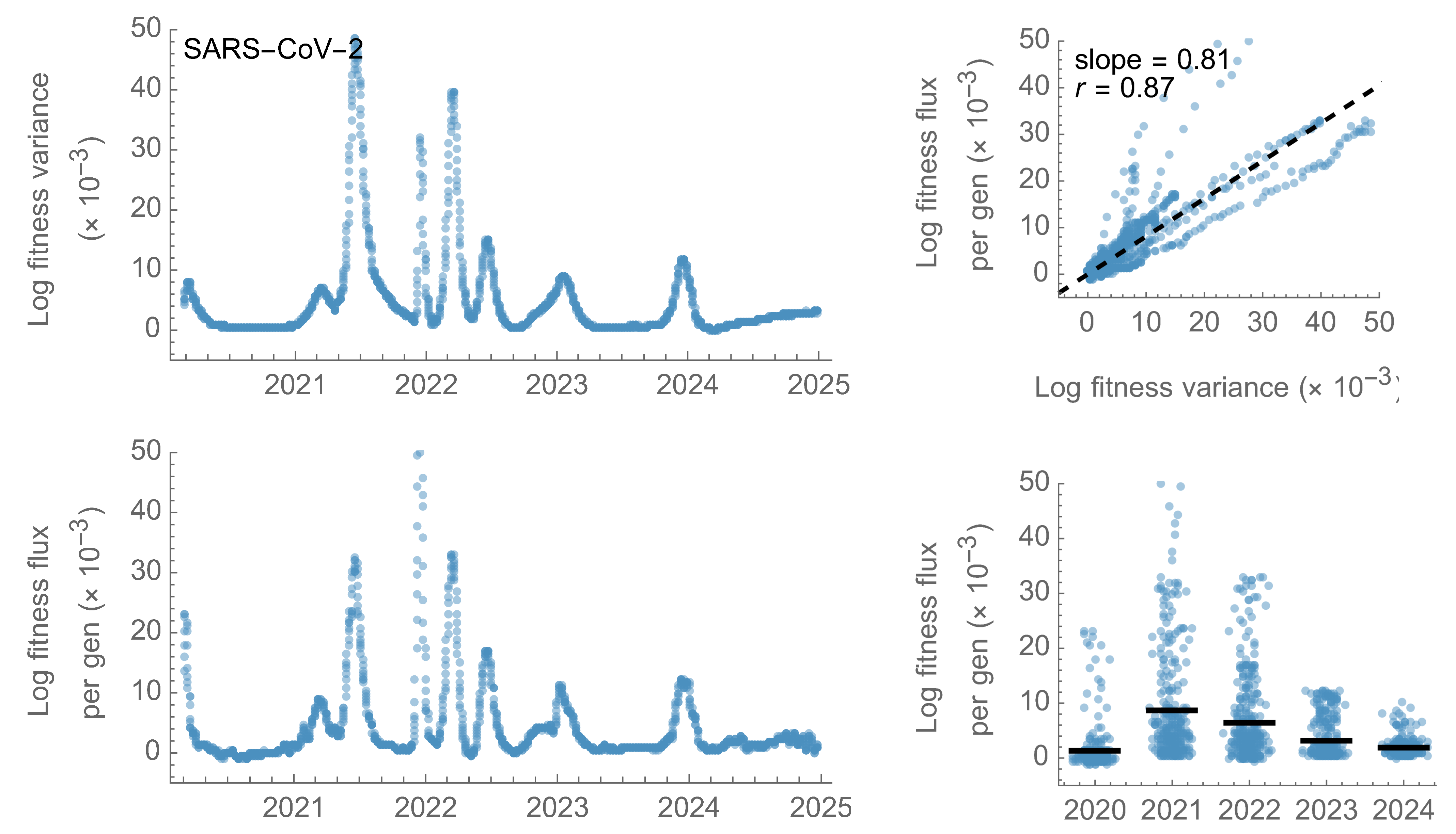
Fitness variance correlates well with fitness flux
This is a specific example of Fisher's fundamental theorem
"The rate of increase in fitness of any organism at any time is equal to
its genetic variance in fitness at that time," ie
$$\frac{d\bar{f}}{dt} = Var(f)$$
Mutational fitness effects
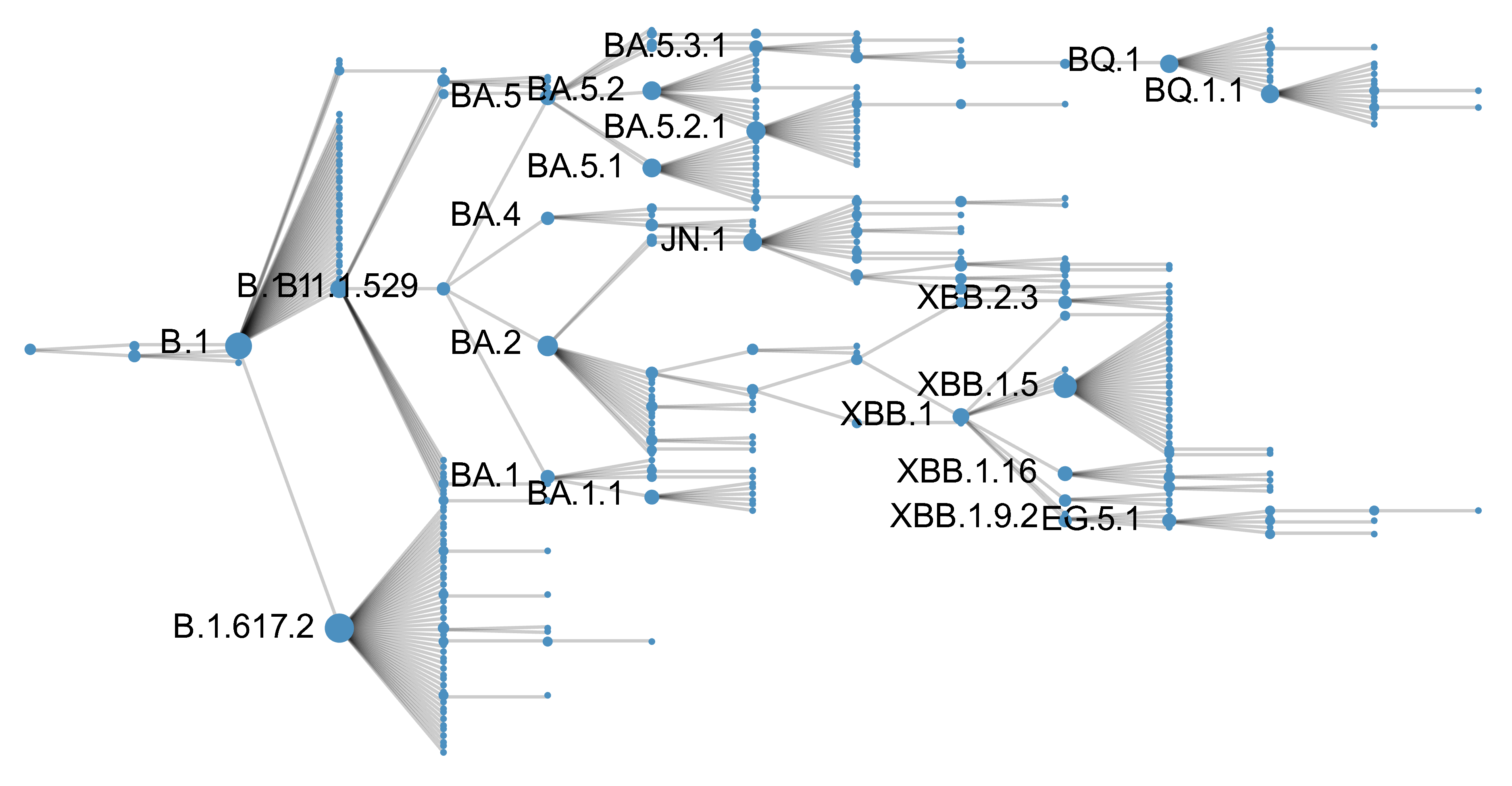
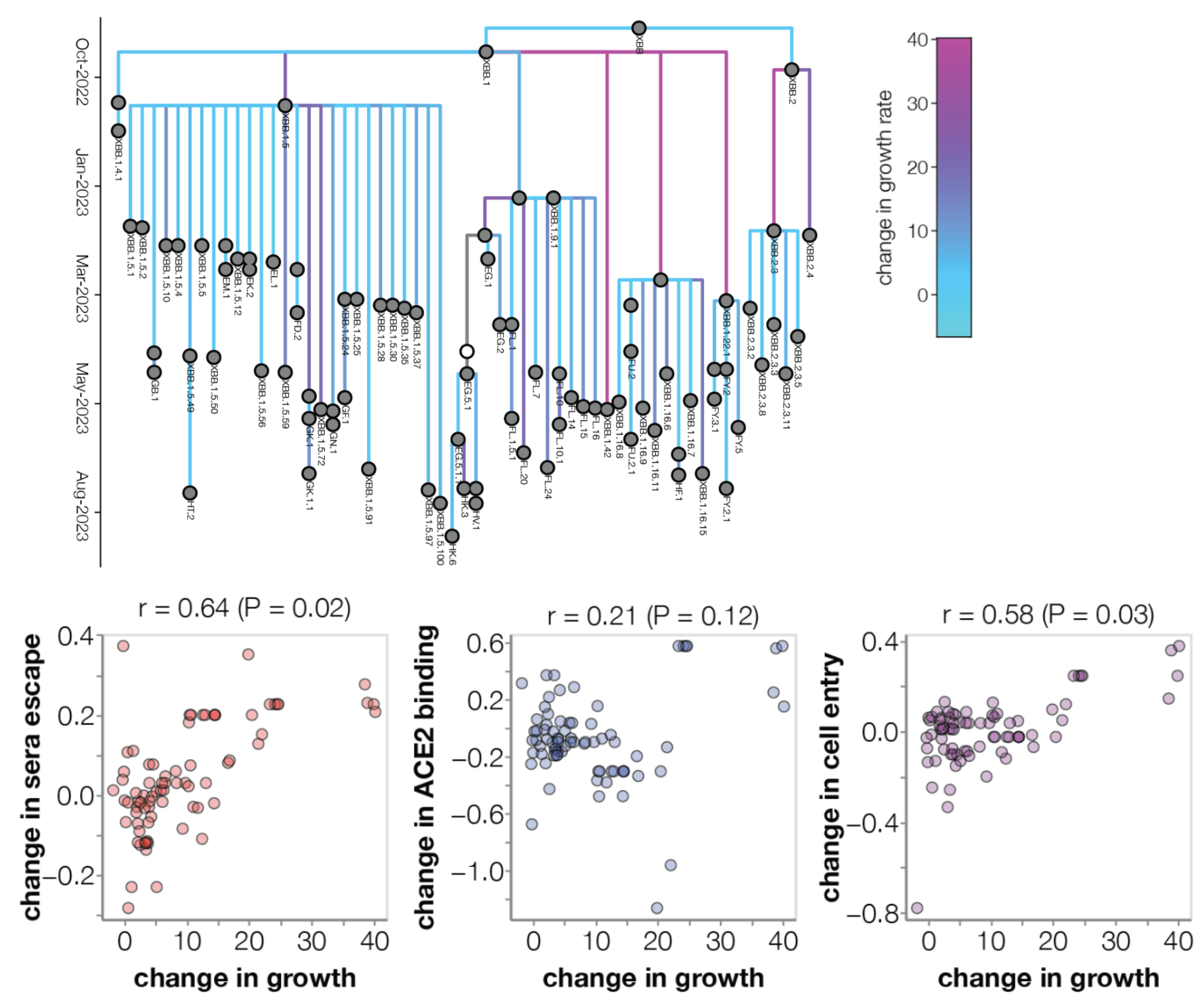
Analyze MLR fitness between parent/child lineages
Expand to 367 Pango lineages with at least 1000 sequence counts in the US from 2020 to 2025
Similar concept to Obermeyer et al
Most Pango branches have 0-1 spike mutations and change log fitness by ±0.1
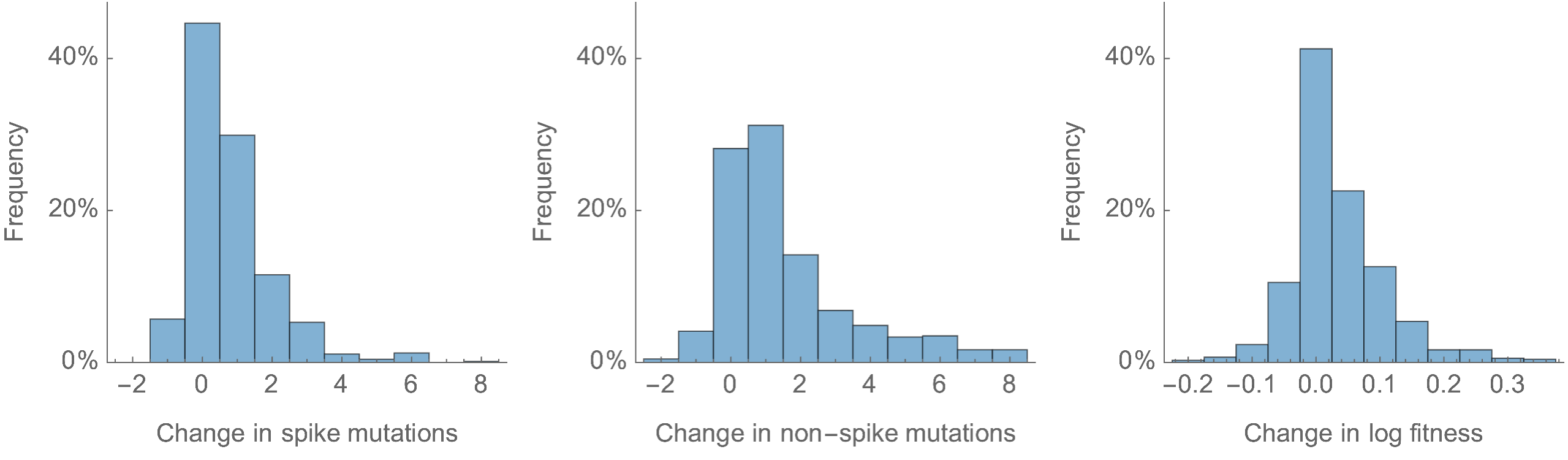
Spike mutations tend to increase fitness
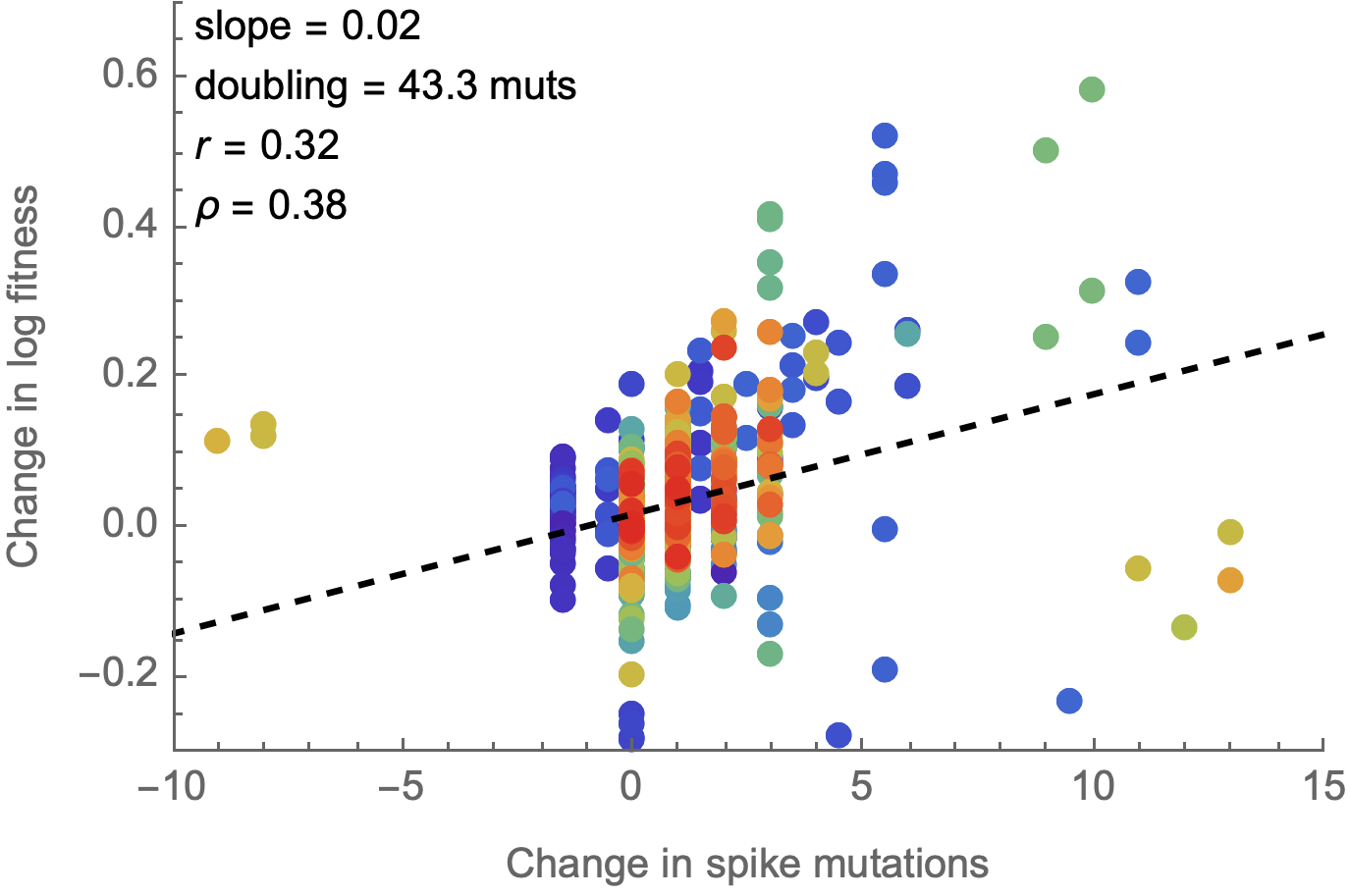
Non-spike mutations do not impact fitness on average
Looking across the genome shows that spike is the focus for positive selection, but accessory genes have some signal


Some attenuation of fitness effects over time
Framework to compare predictors of fitness
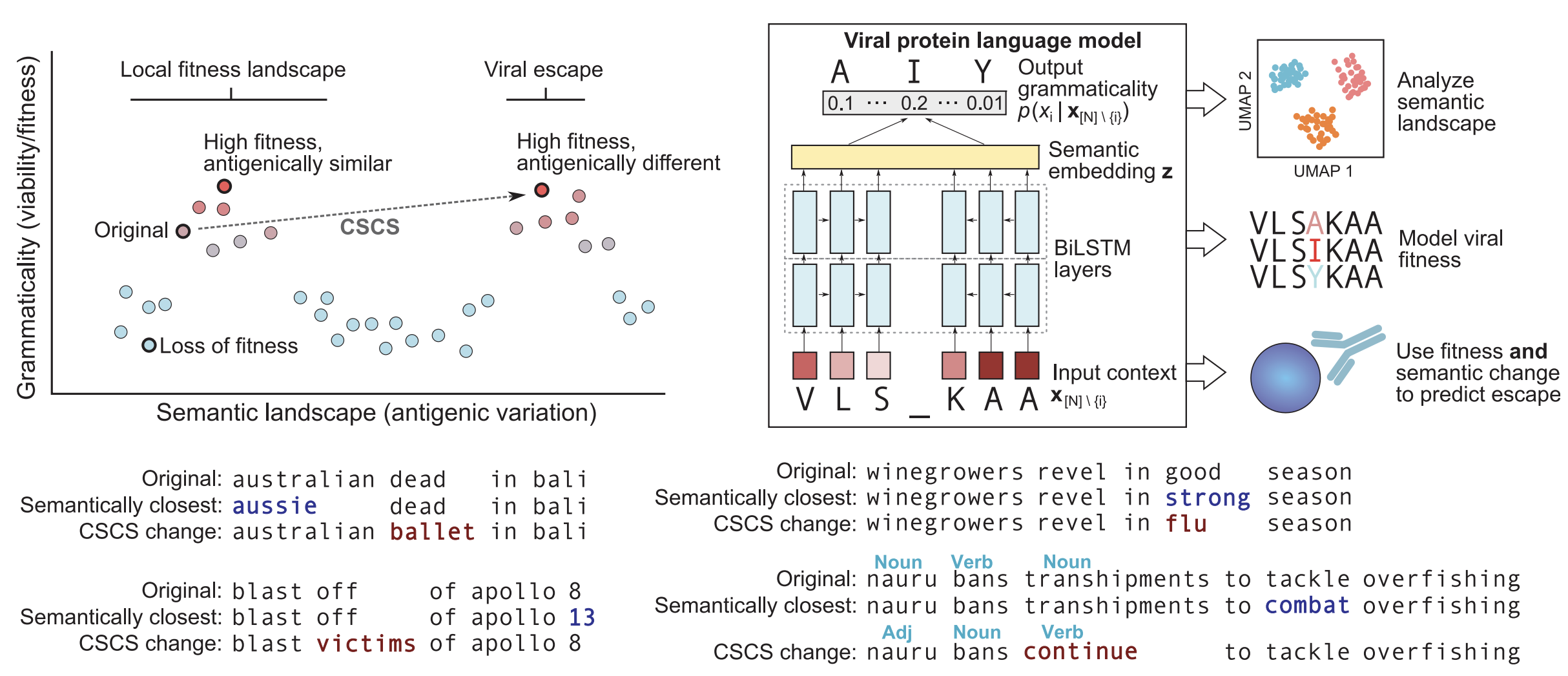
EvEscape is a metric that combines a variational autoencoder for mutation effect + antibody accessibility + biochemical dissimilarity
Framework to compare predictors of fitness
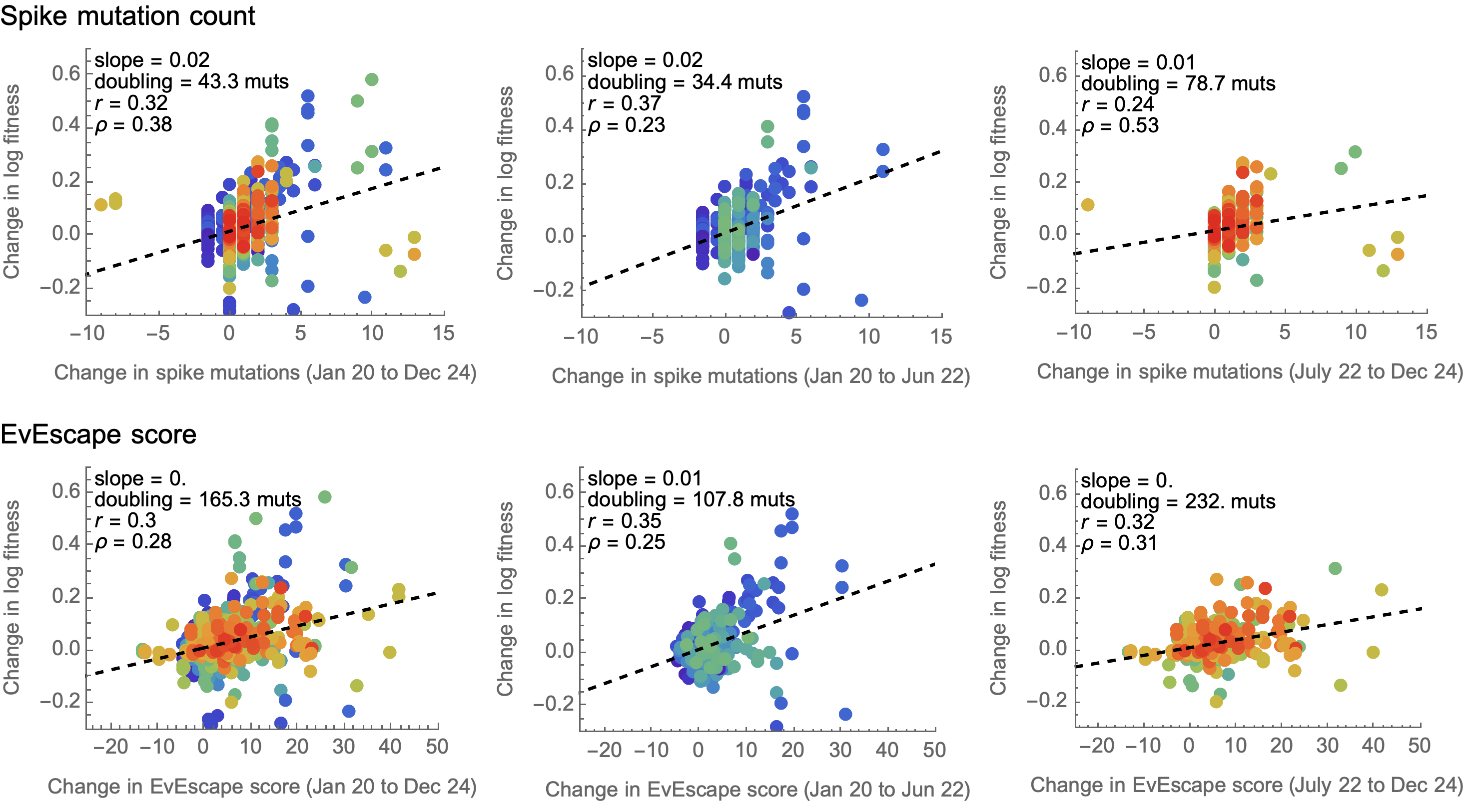
EvEscape does no better than counting spike mutations
Framework to compare predictors of fitness
Semanticity to predict immune escape via dissimilarity of embeddings
Framework to compare predictors of fitness
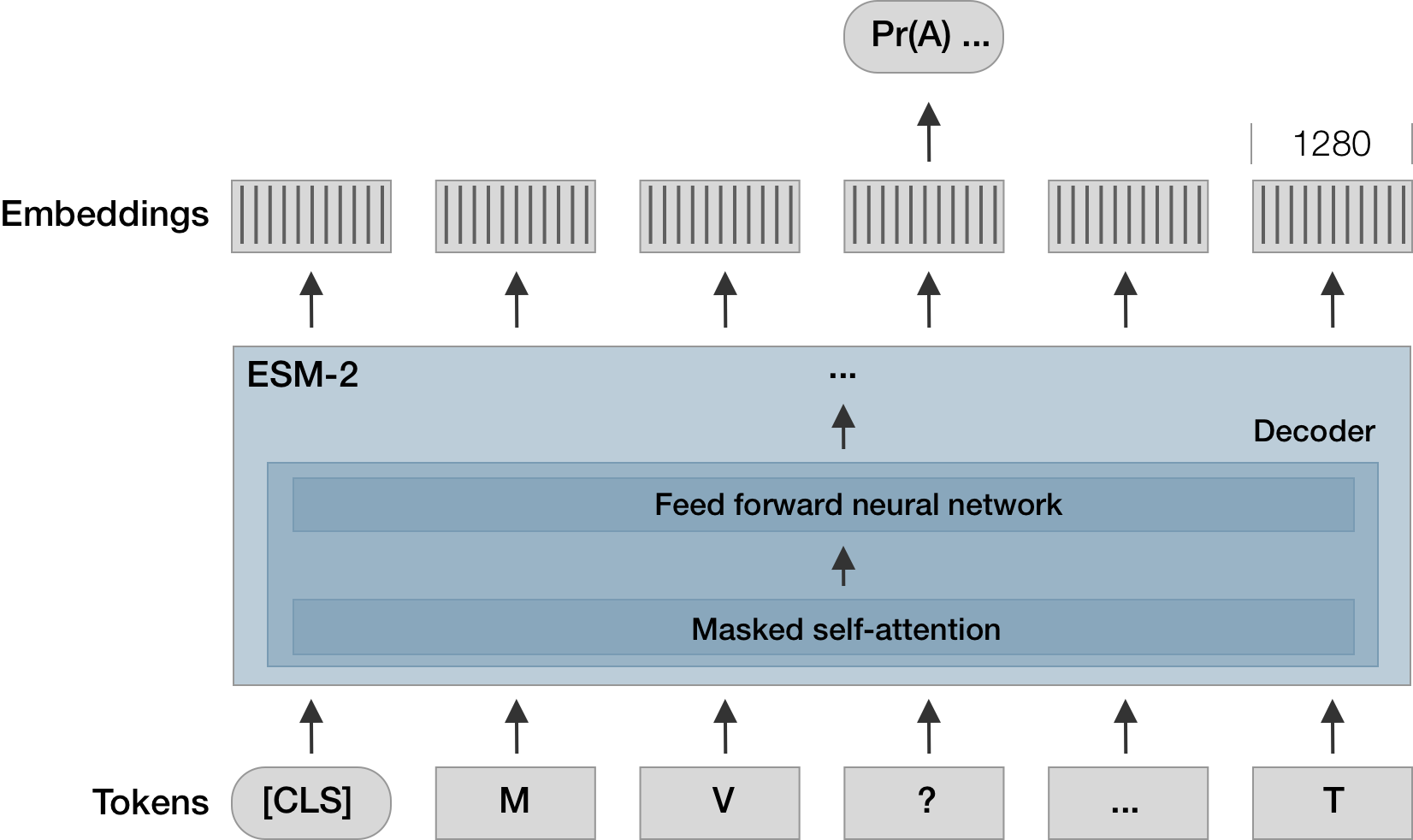
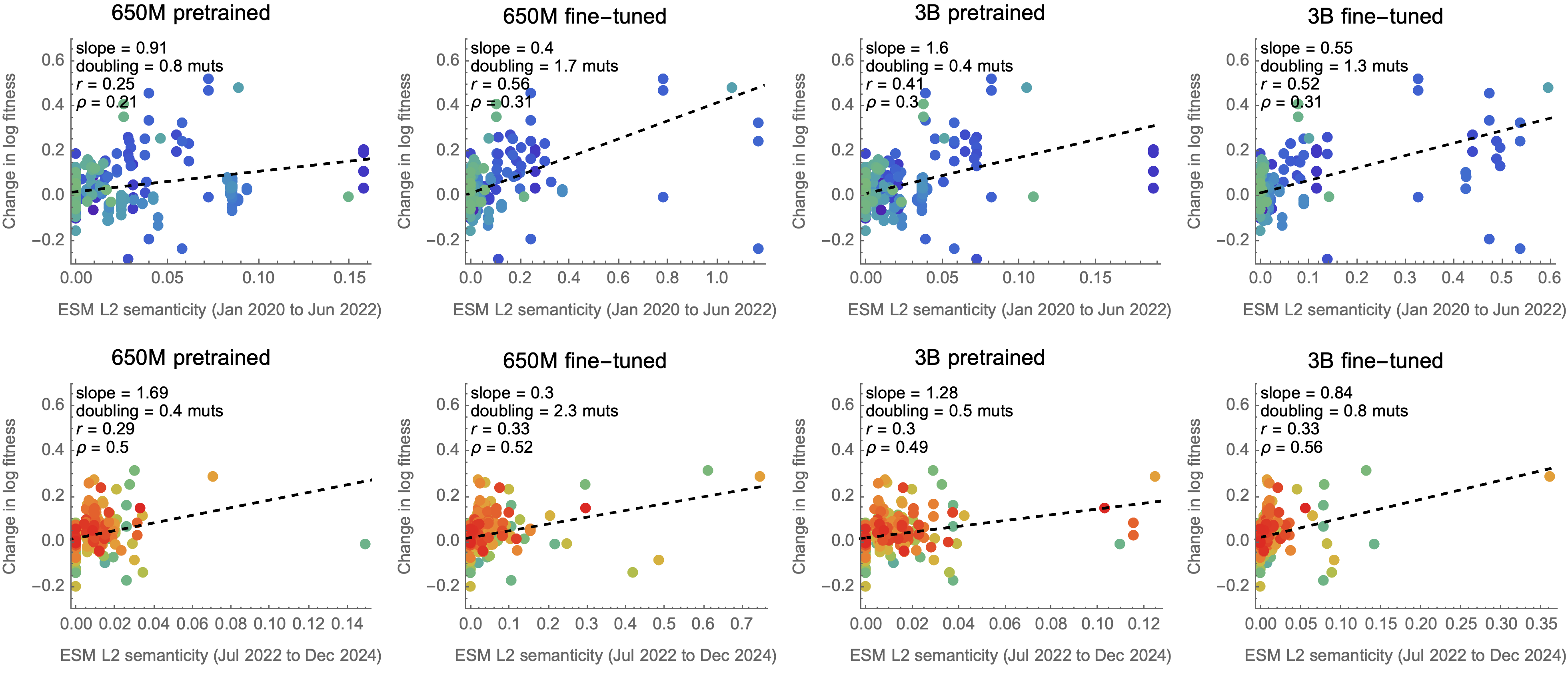
I re-implemented Brian Hie's semanticity metric in ESM-2 via CLS token embedding
Framework to compare predictors of fitness
Semantic dissimilarity does no better than counting spike mutations
Simple linear model to combine predictors into a fitness estimate
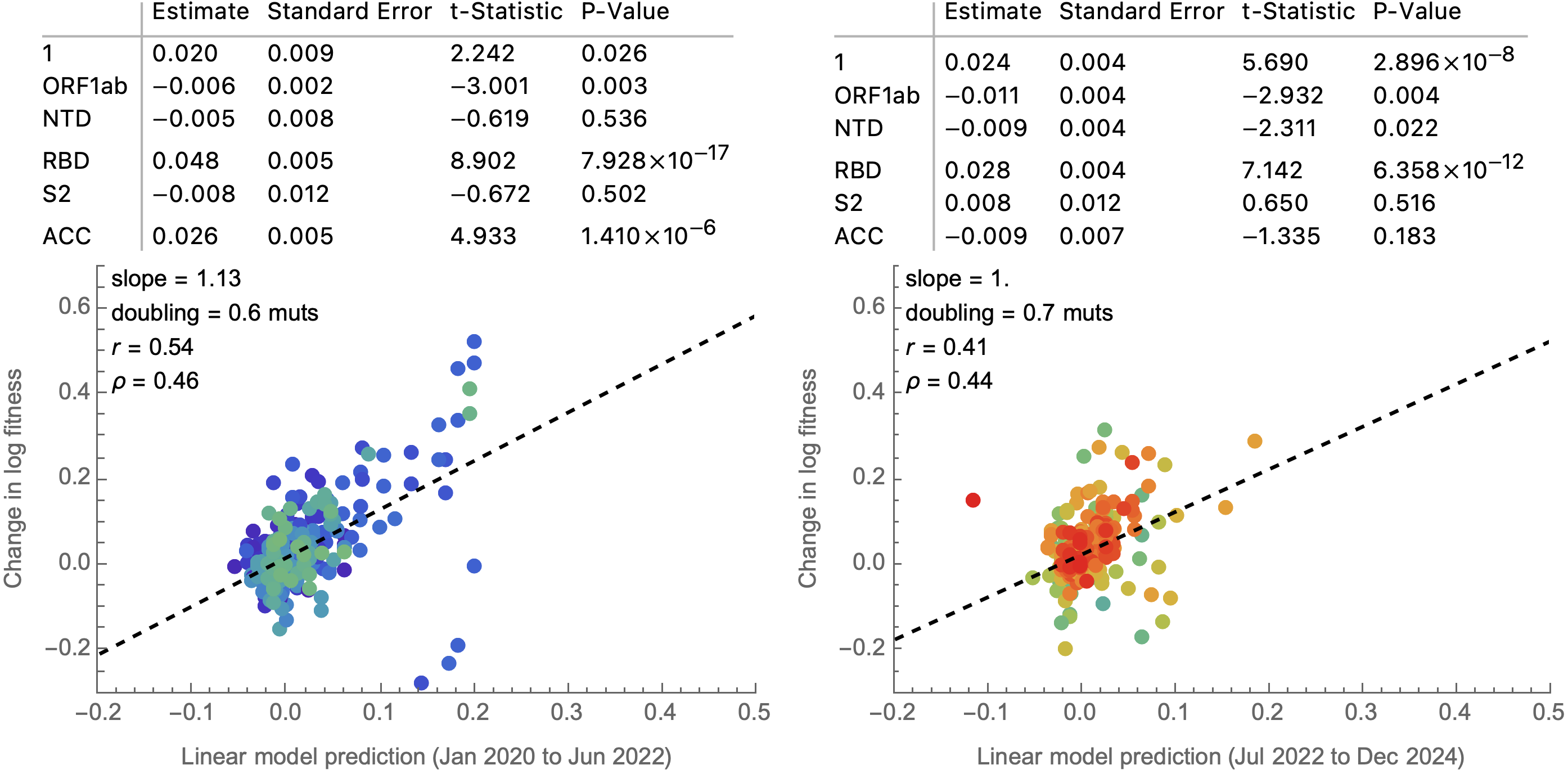
Ongoing work by Bloom Lab to conduct high-throughput experimental measurements of ACE2 binding and immune escape
Prediction of variant fitness from empirical priors
Rather than estimate variant specific fitness $f_i$ directly, instead parameterize the "innovation" in fitness in going from parent lineage $p$ to child lineage $i$ as $\delta_i = (f_i - f_p)$.
Compare a non-informative model of $$\delta_i = (f_i - f_p) \sim \mathrm{Normal}(0, \sigma)$$ to a model where each "innovation" value has an informed prior based on a linear combination of predictors such as ACE2 binding, immune escape and spike mutations, where $z_k$ represents the value of predictor $k$ $$\delta_i = (f_i - f_p) \sim \mathrm{Normal}\left(\sum_k \beta_k \, z_k, \sigma\right)$$
Still need approaches that explicitly model mutations and emergence of novel lineages
Acknowledgements
We're hiring! Particularly interested in recruiting a postdoc to work on sequence language models, but would love to hear from others as well
Seasonal influenza and SARS-CoV-2 genomics: Data producers from all over the world, GISAID
Nextstrain: Richard Neher, Ivan Aksamentov, John SJ Anderson, Kim Andrews, Jennifer Chang, James Hadfield, Emma Hodcroft, John Huddleston, Jover Lee, Victor Lin, Cornelius Roemer, Thomas Sibley
MLR and fitness modeling: Marlin Figgins, Eslam Abousamra, Jover Lee, James Hadfield, John Huddleston, Philippa Steinberg, Jesse Bloom, Cornelius Roemer, Richard Neher
Bedford Lab:
![]() John Huddleston,
John Huddleston,
![]() James Hadfield,
James Hadfield,
![]() Katie Kistler,
Katie Kistler,
![]() Thomas Sibley,
Thomas Sibley,
![]() Jover Lee,
Jover Lee,
![]() Marlin Figgins,
Marlin Figgins,
![]() Victor Lin,
Victor Lin,
![]() Jennifer Chang,
Jennifer Chang,
![]() Nashwa Ahmed,
Nashwa Ahmed,
![]() Cécile Tran Kiem,
Cécile Tran Kiem,
![]() Kim Andrews,
Kim Andrews,
![]() Cristian Ovaduic,
Cristian Ovaduic,
![]() Philippa Steinberg,
Philippa Steinberg,
![]() Jacob Dodds,
Jacob Dodds,
![]() John SJ Anderson
John SJ Anderson
![]() Nobuaki Masaki
Nobuaki Masaki
![]() Amin Bemanian
Amin Bemanian




