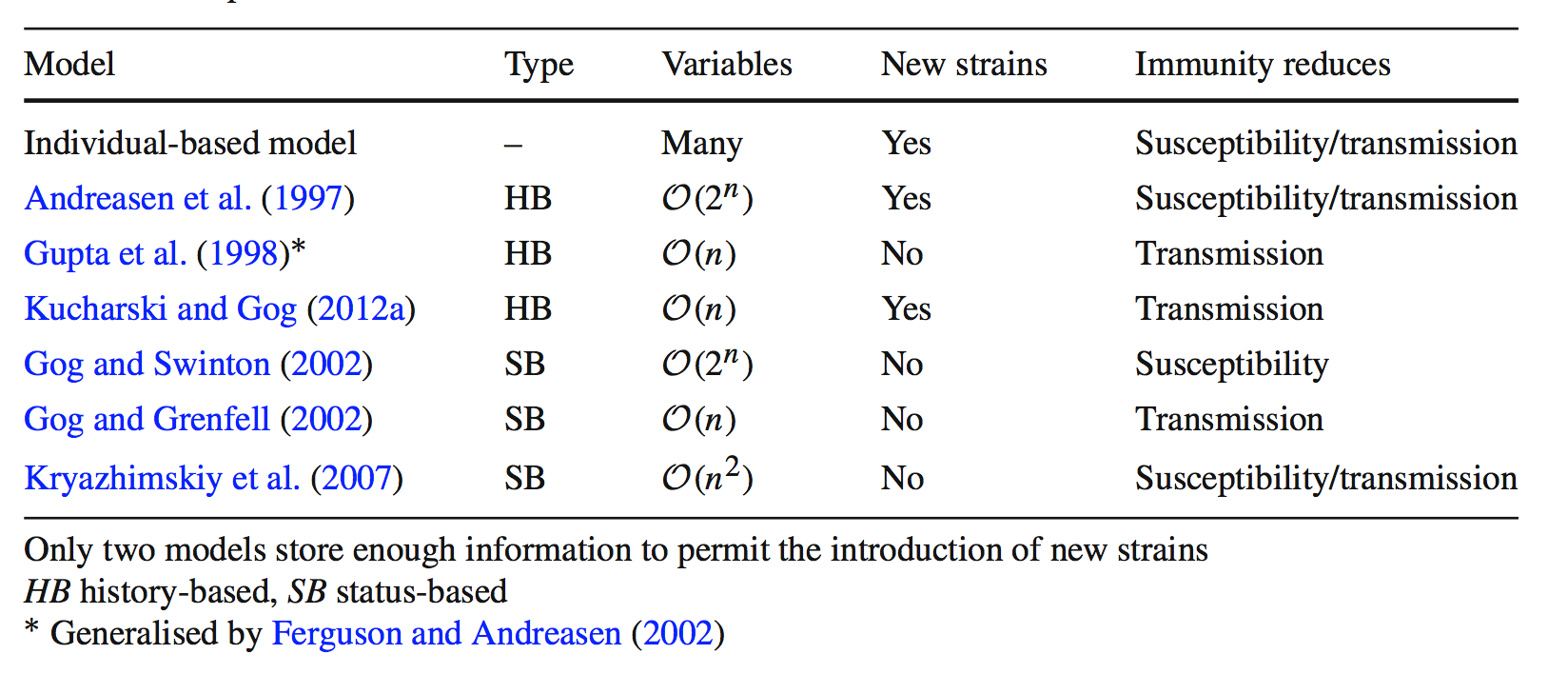
Multistrain models
How to interpret changing trends?
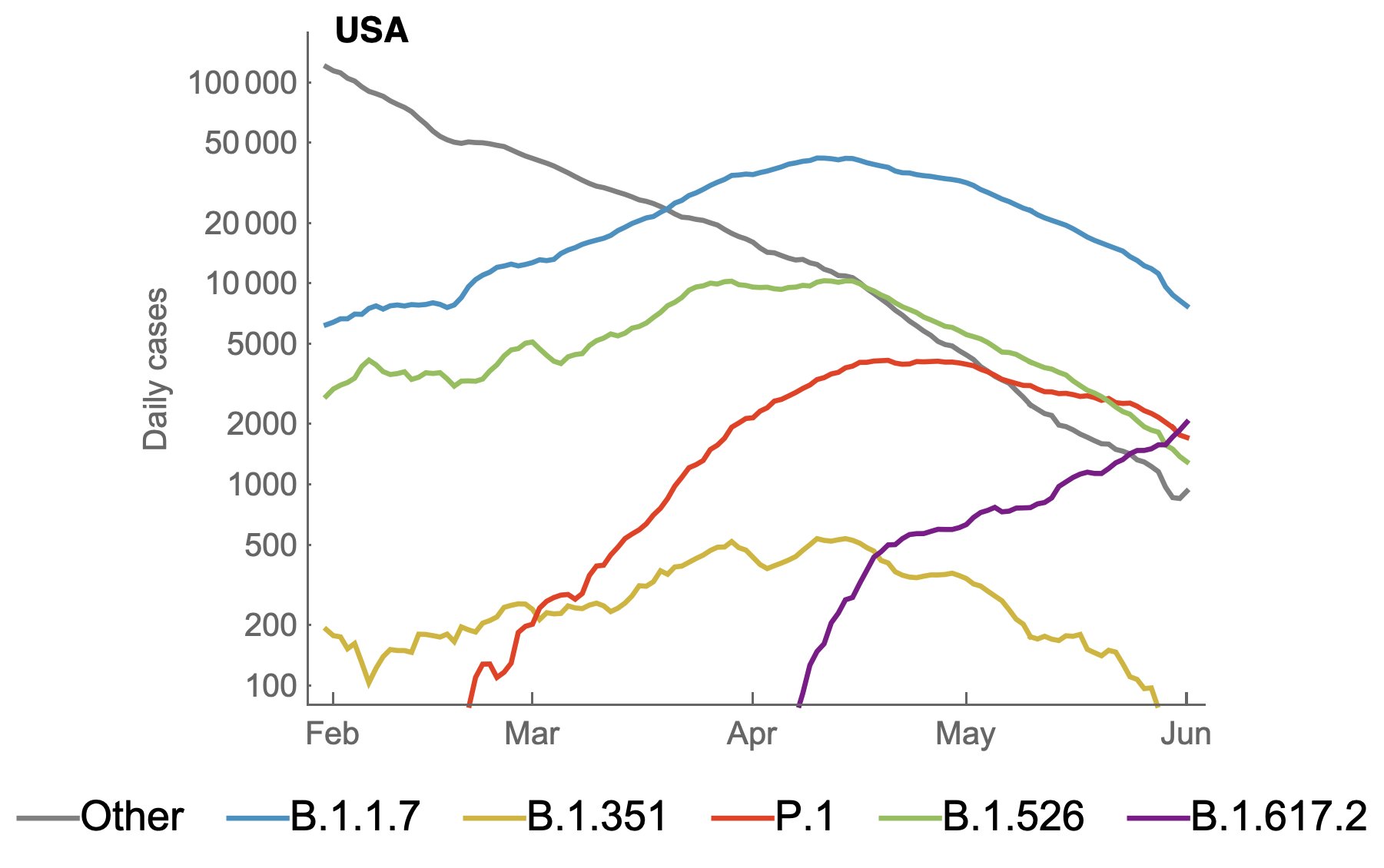
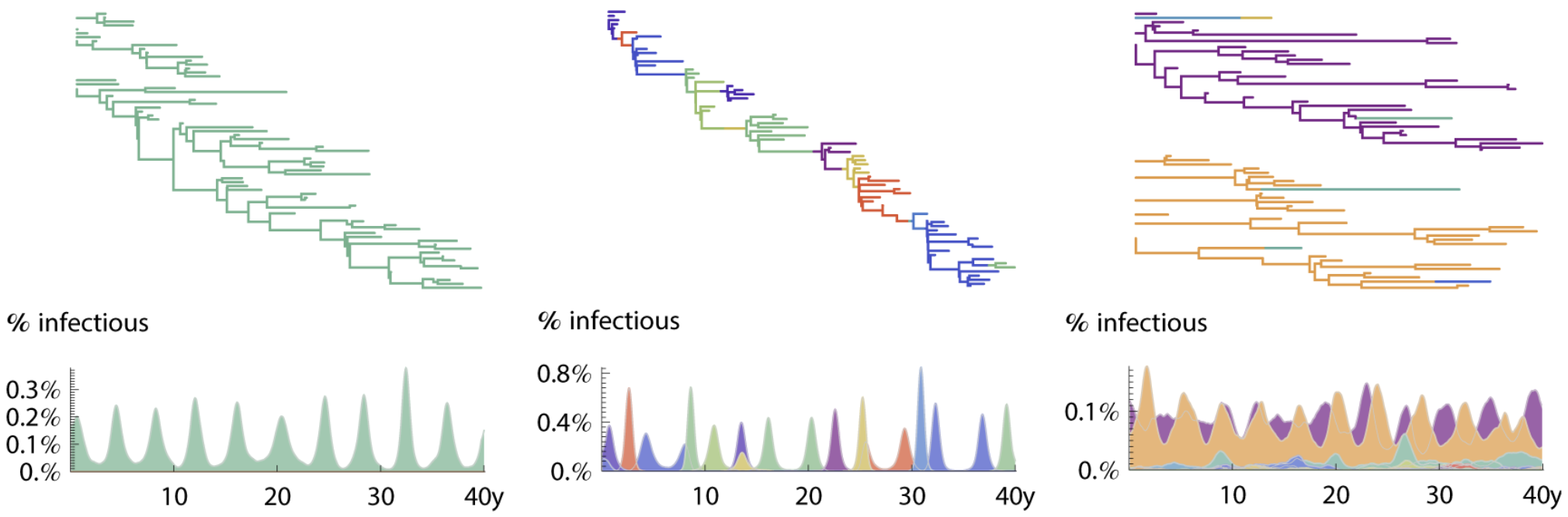
Should we see antigenic change? Turnover? Coexistence?
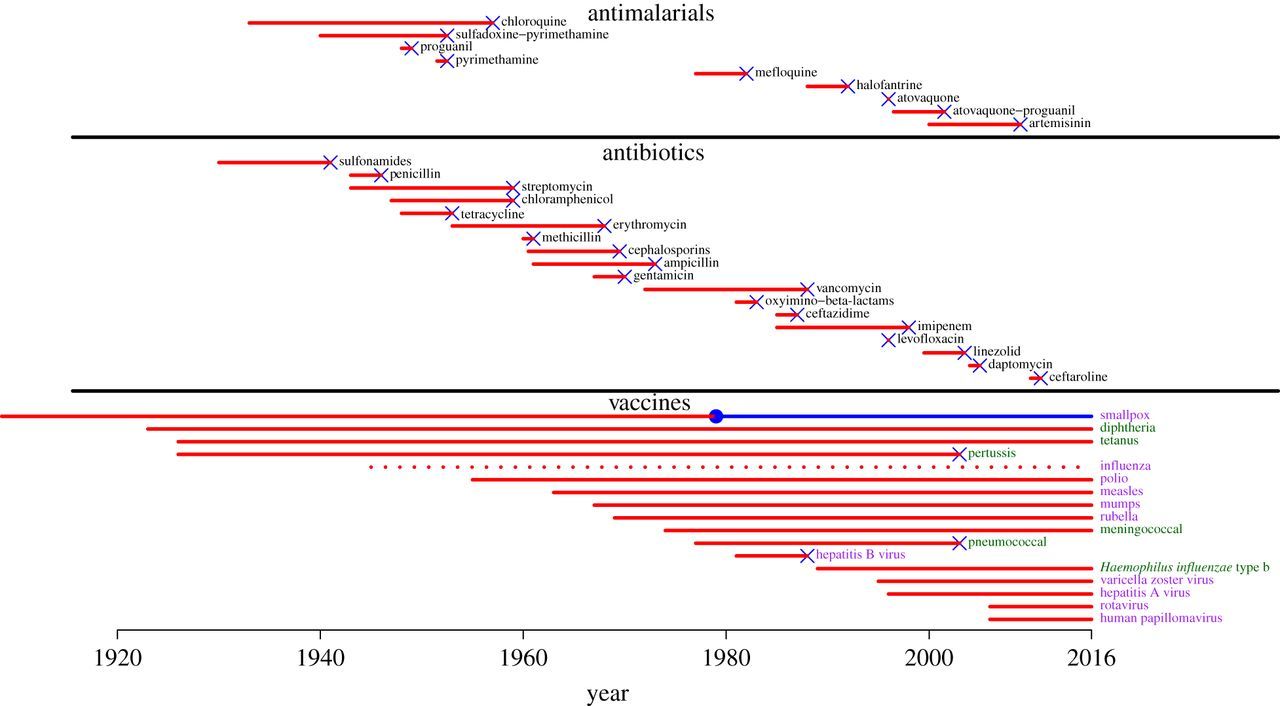
Resistance to vaccines? Antimicrobials?
Model types are fuzzy
Statistical
Mechanistic (mathematical v. agent-based)
Advantages and disadvantages of each?
History-based models
Track individuals' histories of infection, $S_{(0)}, S_{(1)}, S_{(1,2)},...$
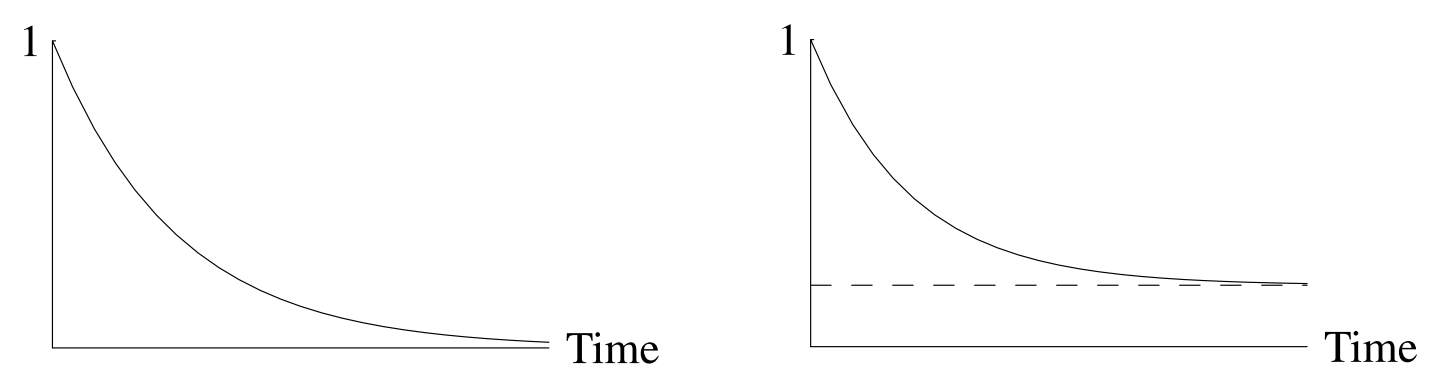
Cross-immunity reduces probability of infection or infectiousness
Numerically unwieldy: $2^n$ histories for $n$ strains
Dimensional reduction
Requires cross-immunity through reduced transmission (only)
Cross-immunity must be in context of antigenic "neighborhoods"
(with $n$ strains in $m$ neighborhoods, system is $n$ x $(m+1)$)
Impossible to calculate immunity to new strains
Status-based models
Track individuals S, I, or R to each strain
$O(n)$ equations possible
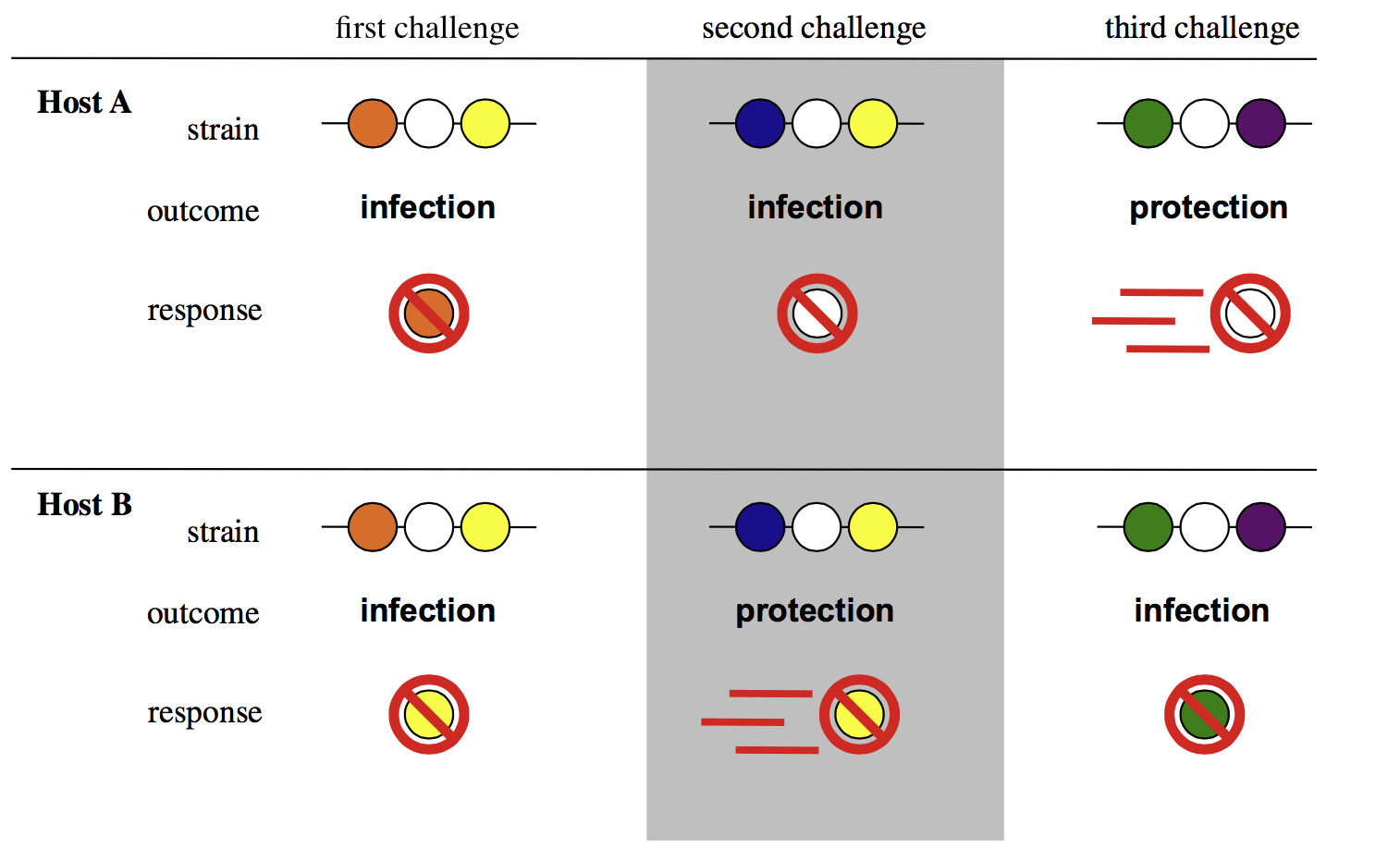
"Polarized" immunity: If $i$ and $j$ cross-react, infection with $j$ leads to perfect immunity to $i$ in some fraction of hosts
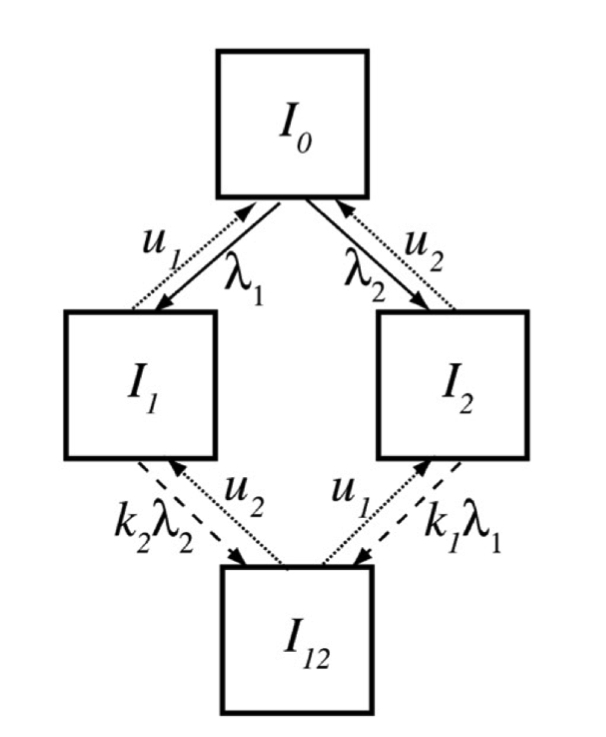
A "simple" status-based model
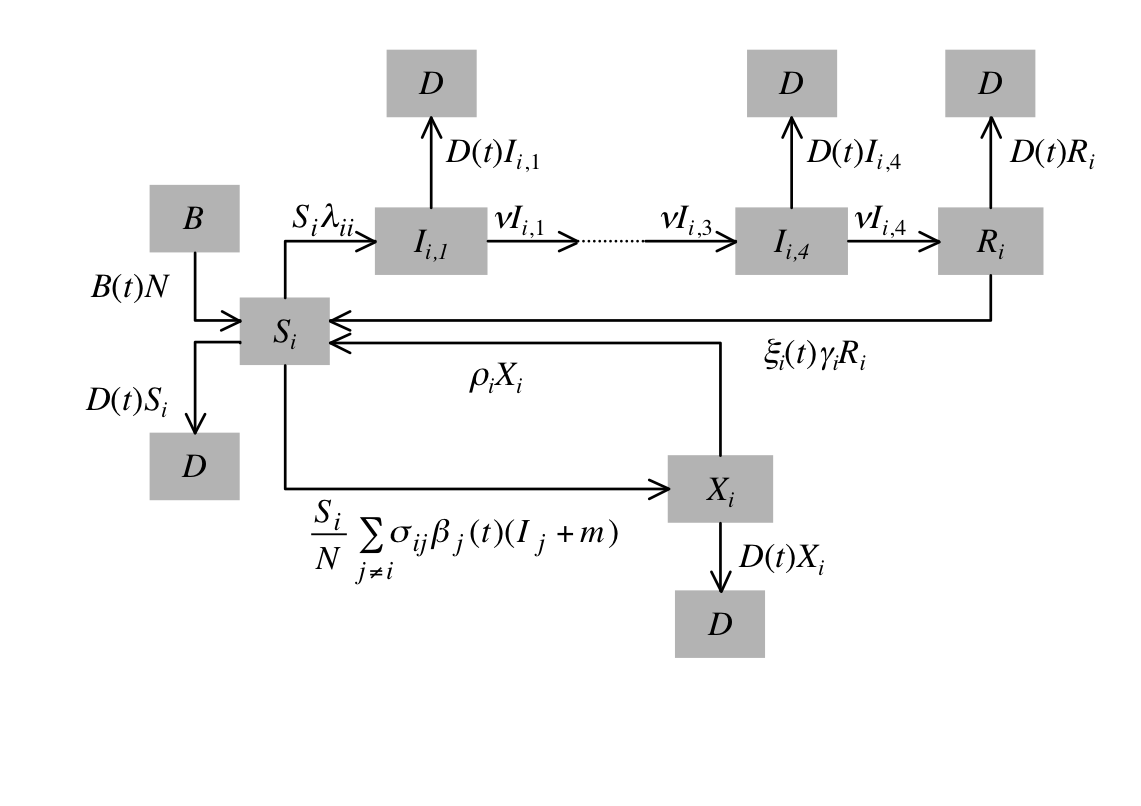
Implicit assumption
Proportion of population not infected by second strain
Some options for multistrain models
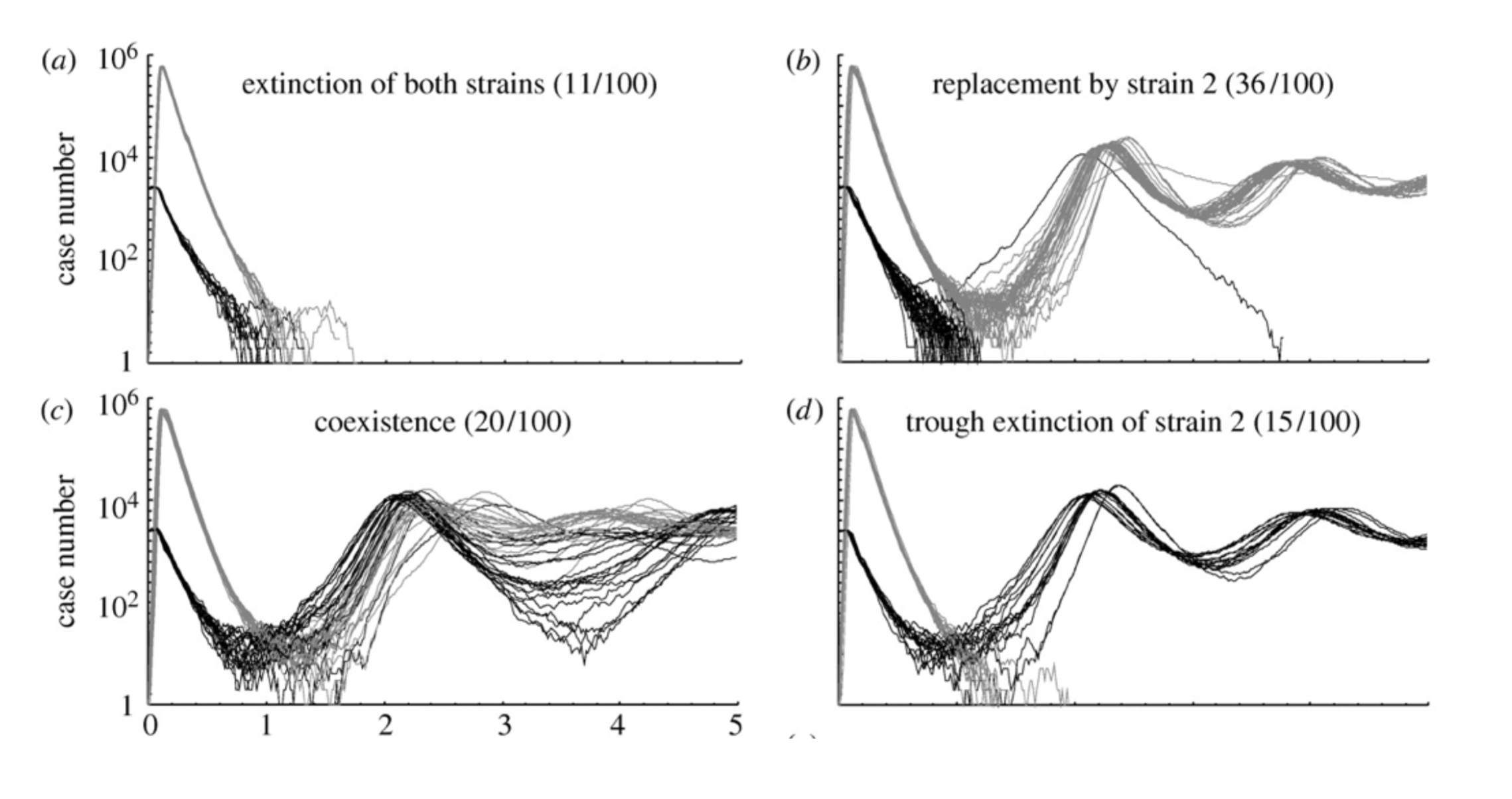
Classic problem: invasion
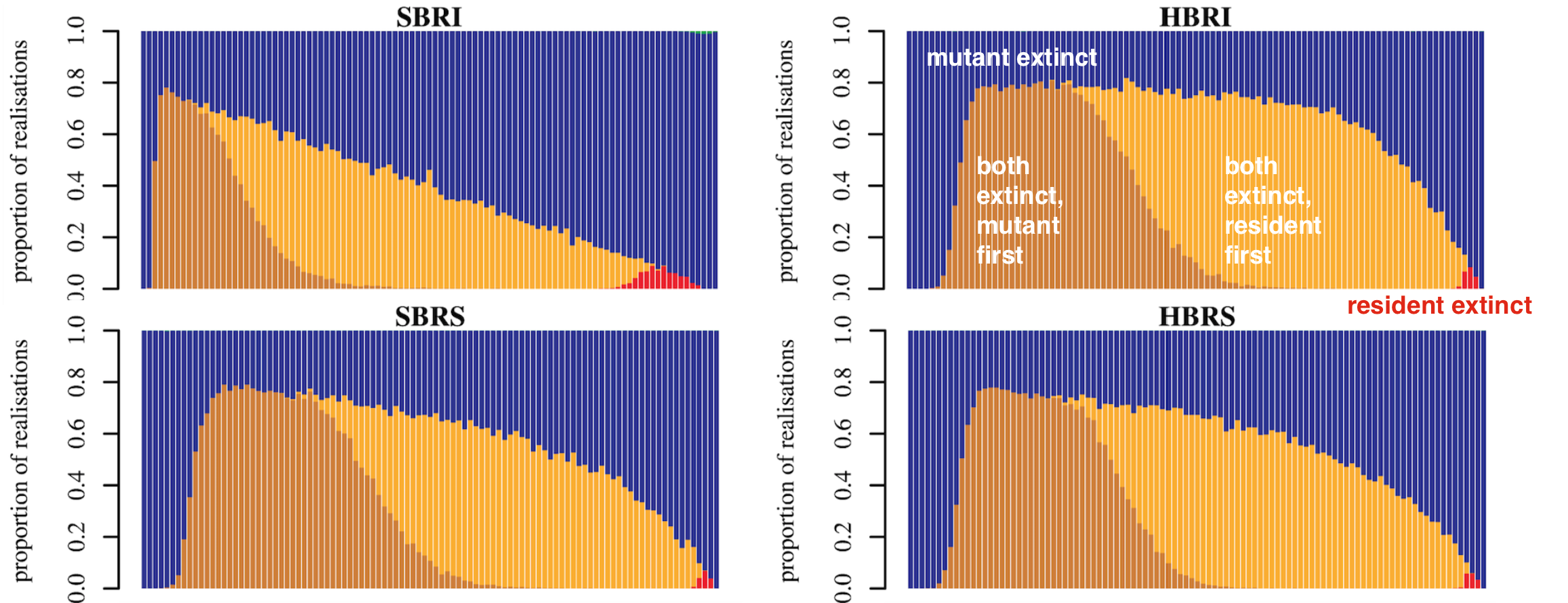
Subtle differences change dynamics
Cross-immunity
Know your assumptions
Which model promotes coexistence?
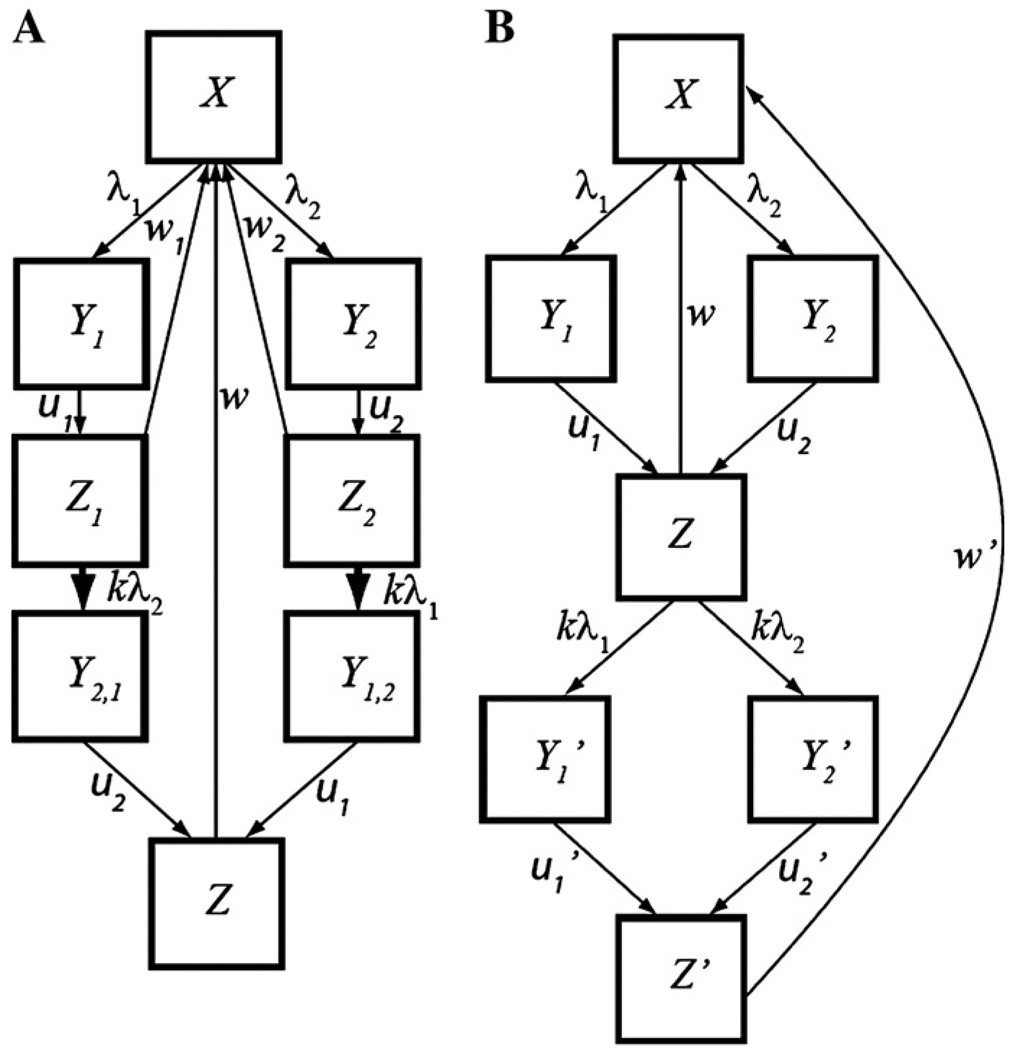
Model A
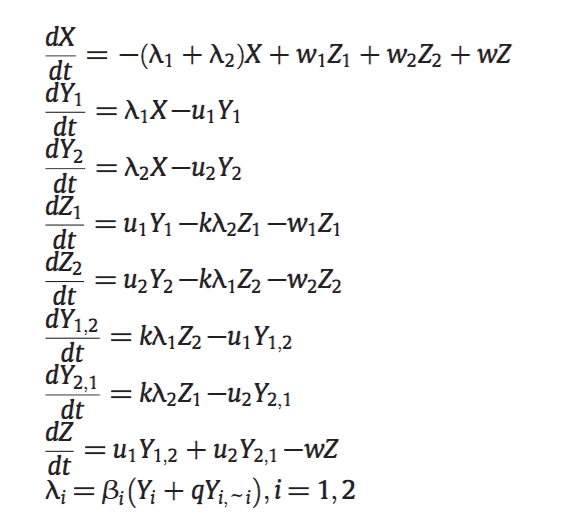
Model B
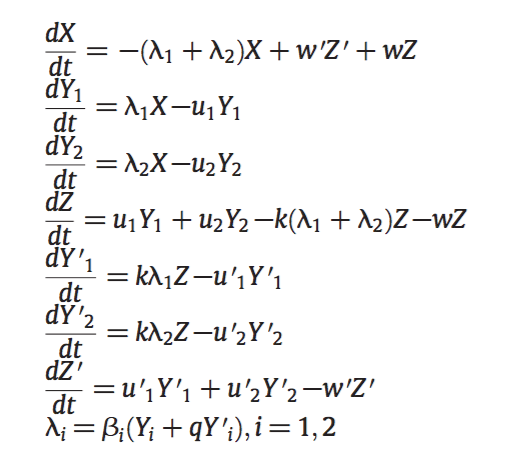
Does this model bias for coexistence?
Equations
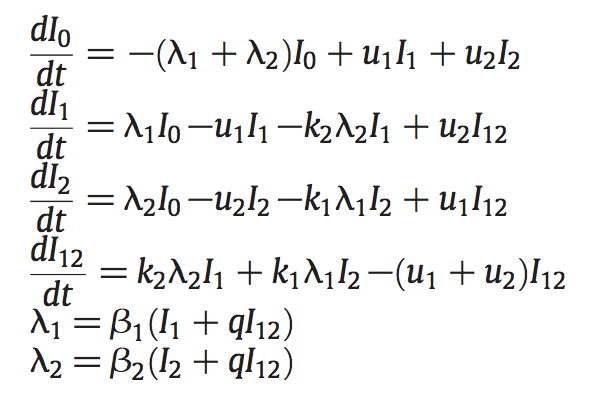
Equations
Ecological dynamics depend on strain composition
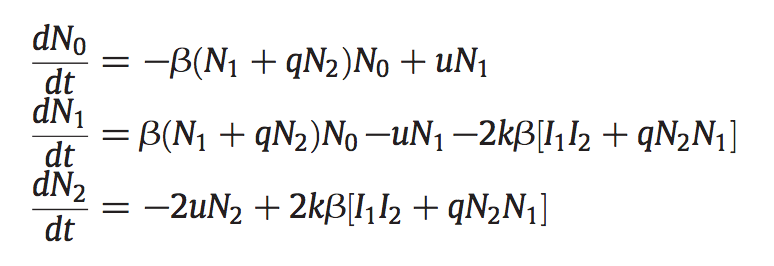
Multiplicity of infection
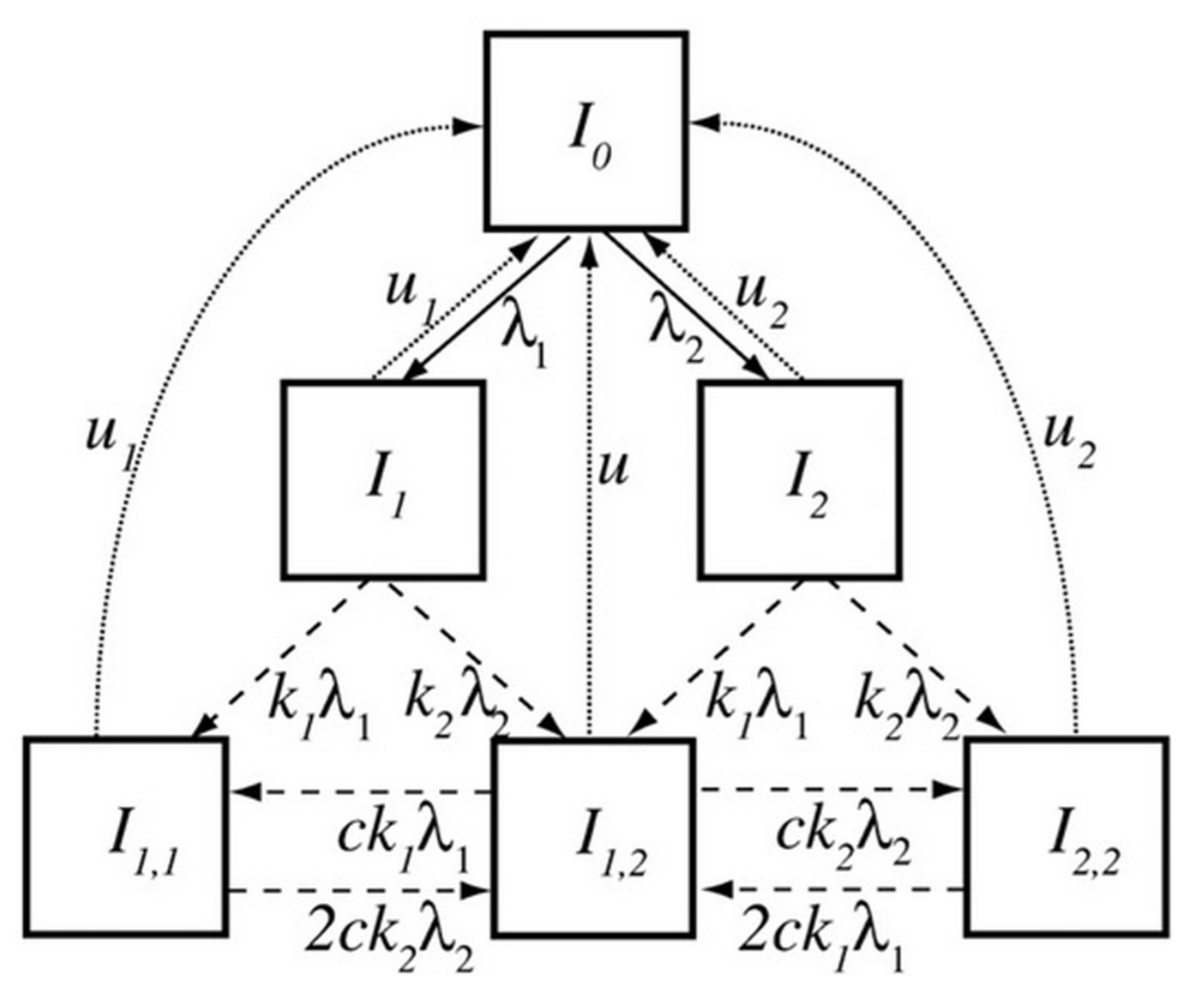
ODEs
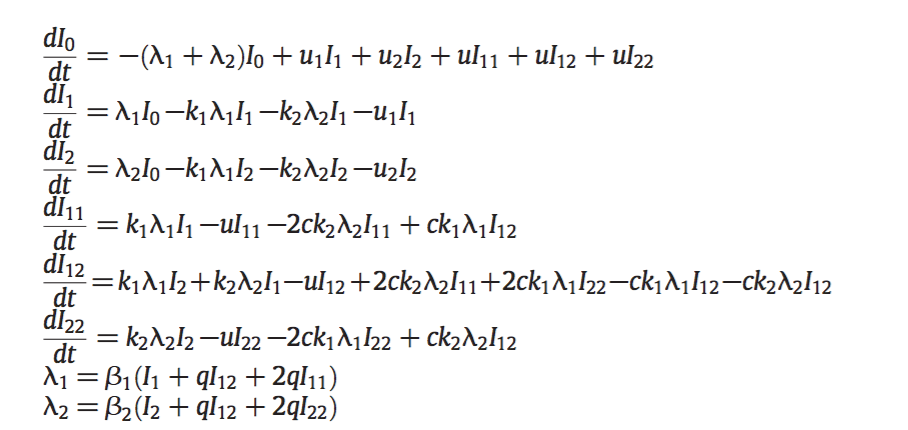
Ecological dynamics
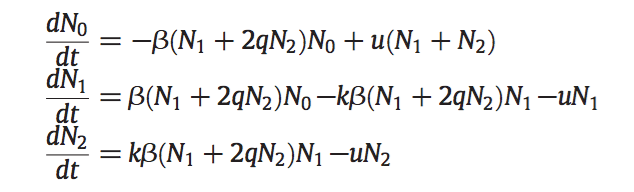
Ancestor tracing
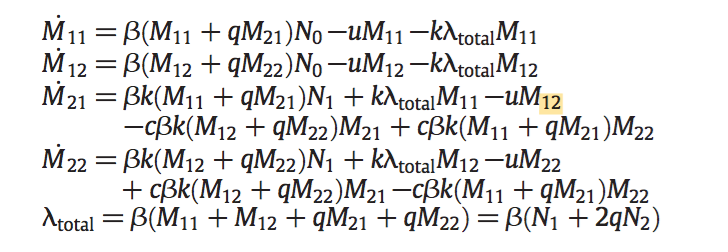
The question of strain space
Continuous or discrete?
How many dimensions?
Continuous space
Discrete space
Immunodominance and breadth affect diversity
Agent-based models
Potentially most efficient with many strains
Support complex interactions
Naturally incorporate demographic stochasticity
Analytic approaches
Equilibria: Solve for $S_{i}'=I_{i}'=...=0$
Stability analysis: Linearize at equilibria
Invasion analysis: Is $I_{2}'>0$ at $I_{1}^*$?
Integration: Calculate $I_{1}(t), I_{2}(t),...$
Numerical integration
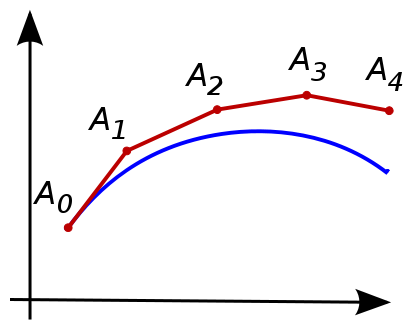
Approximate solution to $N'=f(N)$:
$$N(t_0+\Delta t) \approx N_0+ f(N_0) \Delta t = N_1$$
Re-iterating, we get
$$N_{z+1} \approx N_{z}+f(N_{z}) \Delta t$$
$$N_{z+1} \approx N_{z}+f(N_{z}) \Delta t$$
We could assume $f(x)$ is constant for $\Delta t$ (Euler's method)
Even better, average over multiple points!
A second-order method
$$N_{z+1} \approx N_{z}+f(N_{z}) \Delta t$$
$$M_{z+1}=N_z+f(N_{z}) \Delta t$$
$$N_{z+1}=N_z+\frac{1}{2}\left[ f(N_{z})+f(M_{z+1})\right] \Delta t$$
4th-order Runge-Kutta
$$k_1=f(N_z) \Delta t$$
$$k_2=f\left(N_z+\frac{1}{2}k_1 \right) \Delta t$$
$$k_3=f\left(N_z+\frac{1}{2}k_2 \right) \Delta t$$
$$k_4=f\left(N_z+k_3 \right) \Delta t$$
$$N_{z+1}=N_z+\frac{1}{6}(k_1+2k_2+2k_3+k_4)$$
Why not just pick an extremely small $\Delta t$?
Considerations for multistrain models
Form of immunity (duration, strength, polarity)
Effect of immunity (susceptibility, infectiousness, clearance)
Coinfections and timing of interactions
Accuracy for individuals v. populations
Dimensionality and discretization of strain space
Analytic and numeric approaches, including stochasticity