Introduction to phylogenetics
Erick Matsen
(With a great exercise from Trevor)
What is phylogenetics?
“data”: sequence alignment

Sequence alignment is hard!
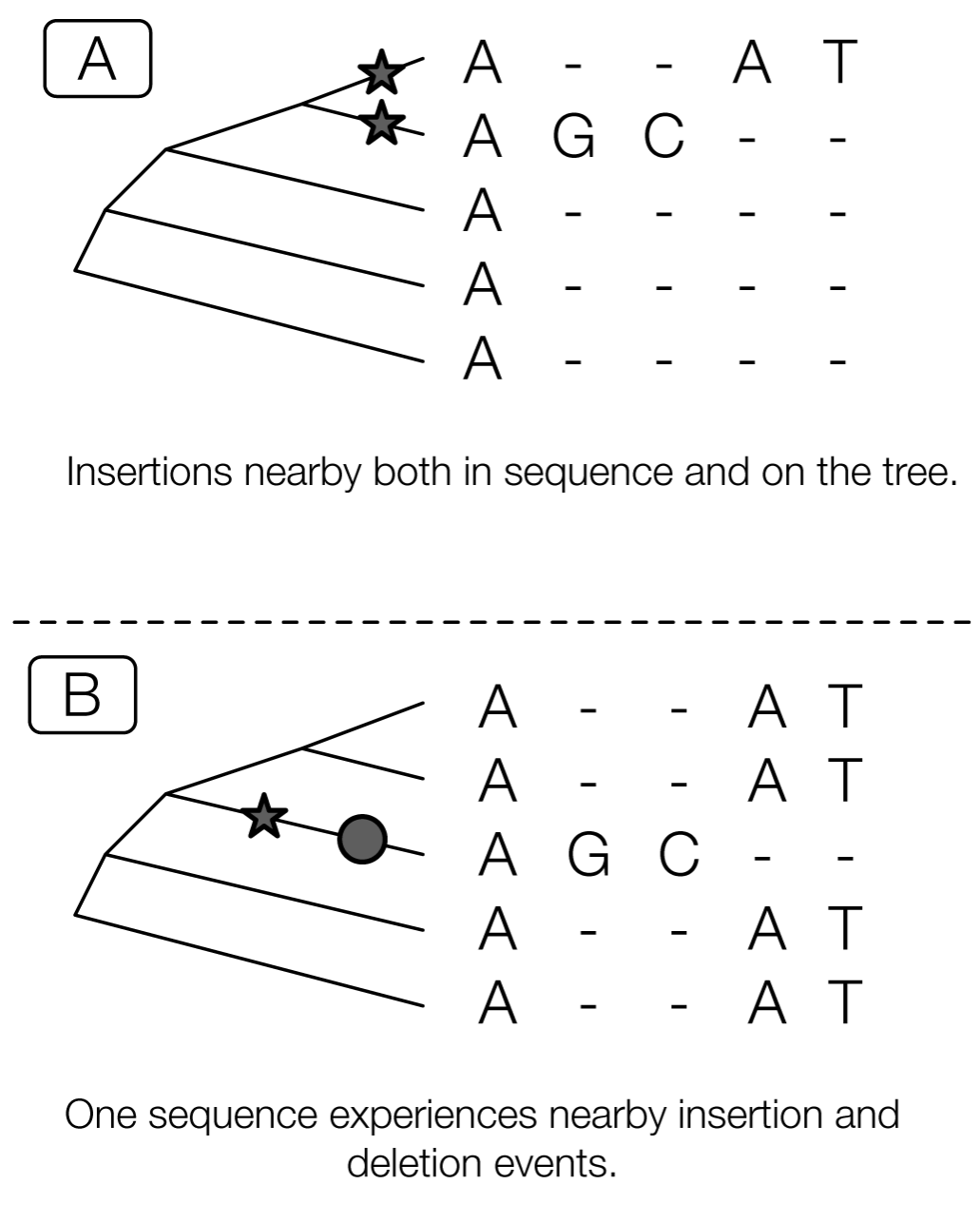
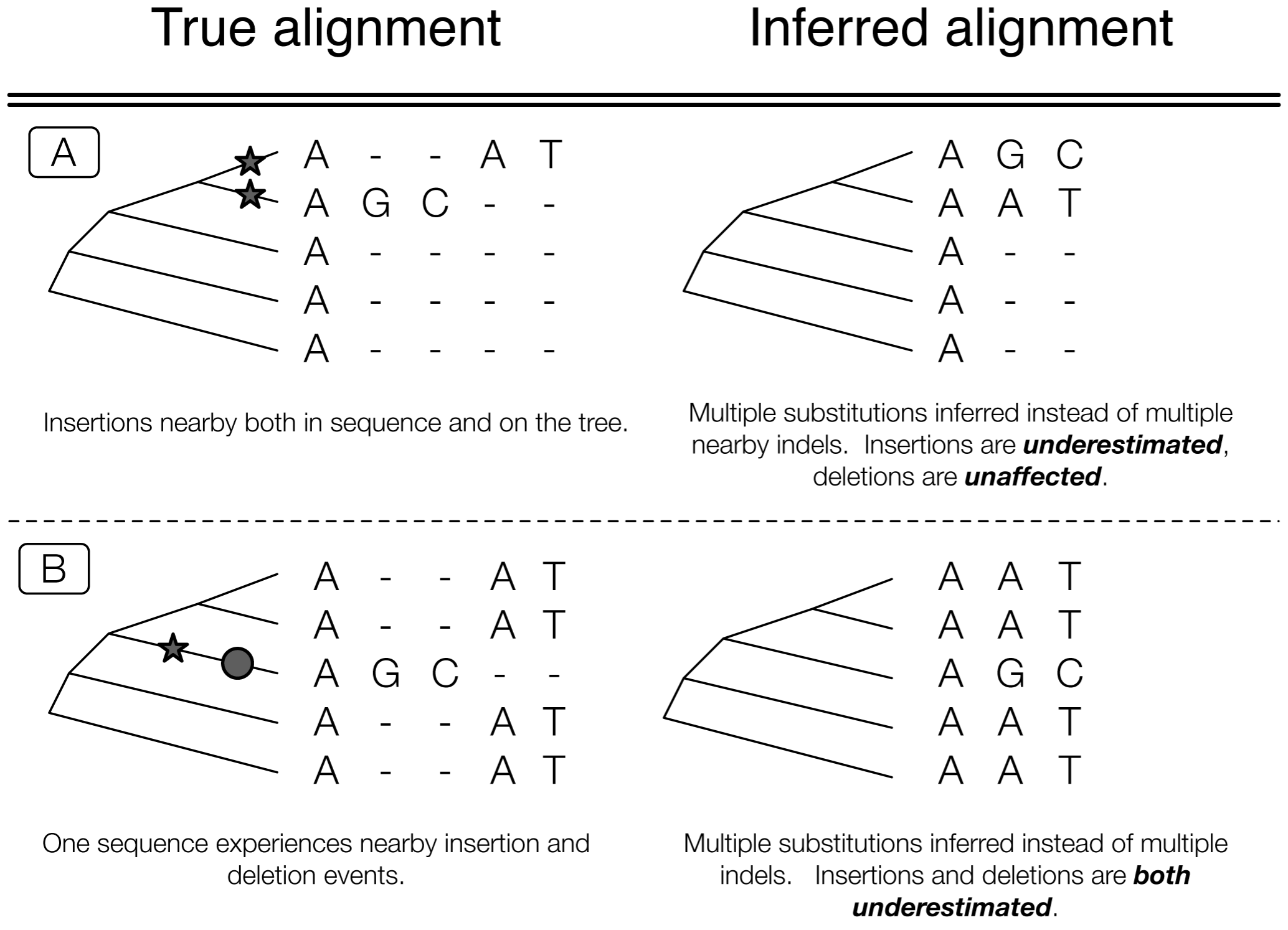
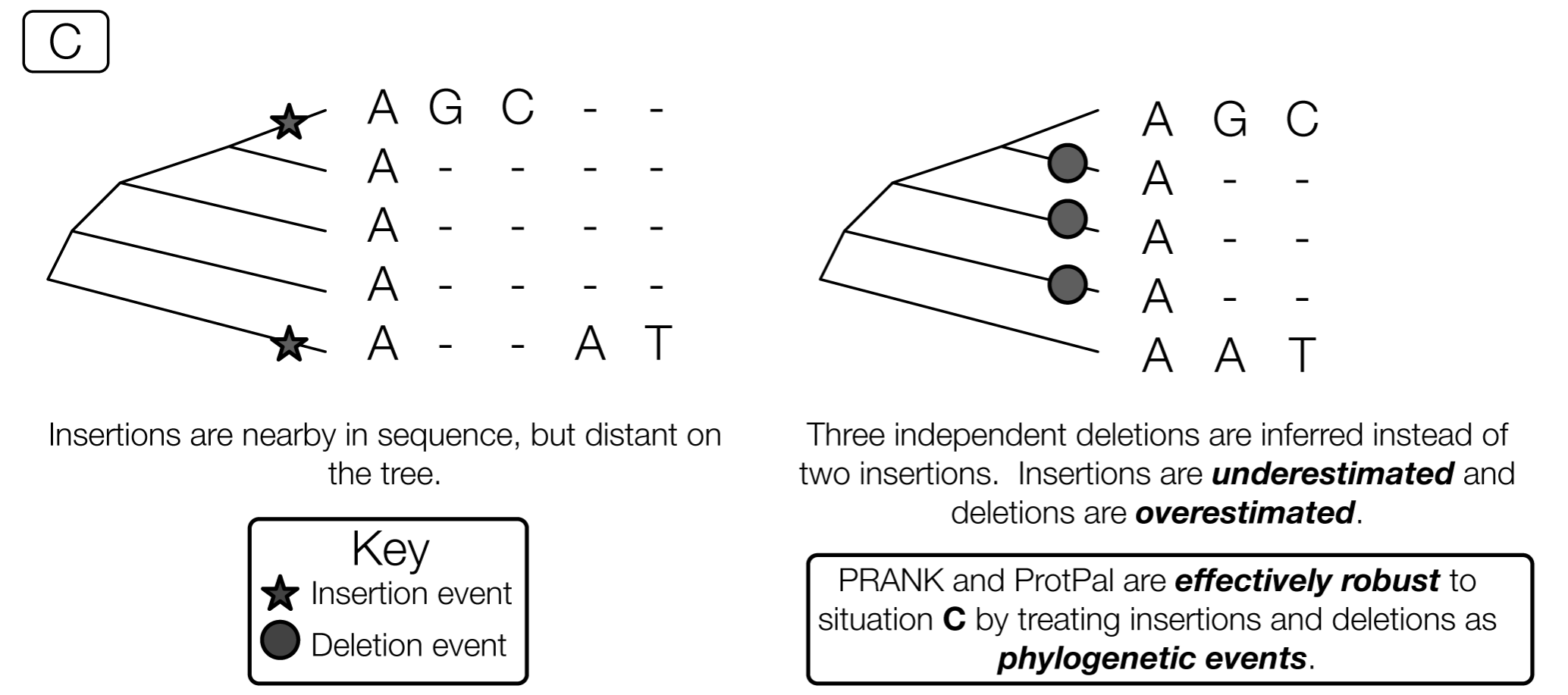
Sometimes it’s more or less impossible
Phylogenetic approach is best
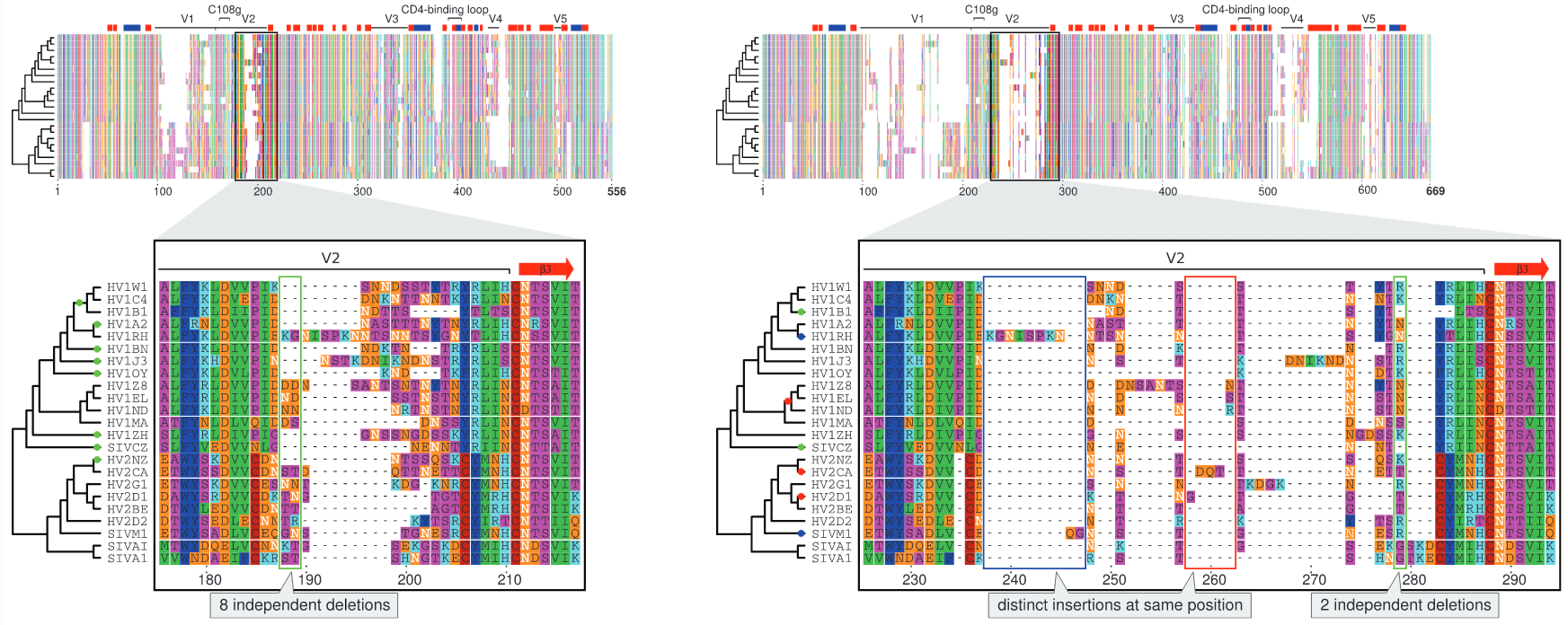
Muscle vs PRANK
BAli-Phy
Co-estimate tree & alignment using Bayesian methods 
Multiple sequence alignment: summary
Types of phylogenetic inference methods
- Distance-based
- Parsimony
- Likelihood-based
- Maximum likelihood
- Bayesian
Distance-based phylogenetics
Parsimony phylogenetics
Parsimony is based on Occam's razor
Among competing hypotheses that predict equally well, the one with the fewest assumptions should be selected.
(The next few slides are from Trevor.)
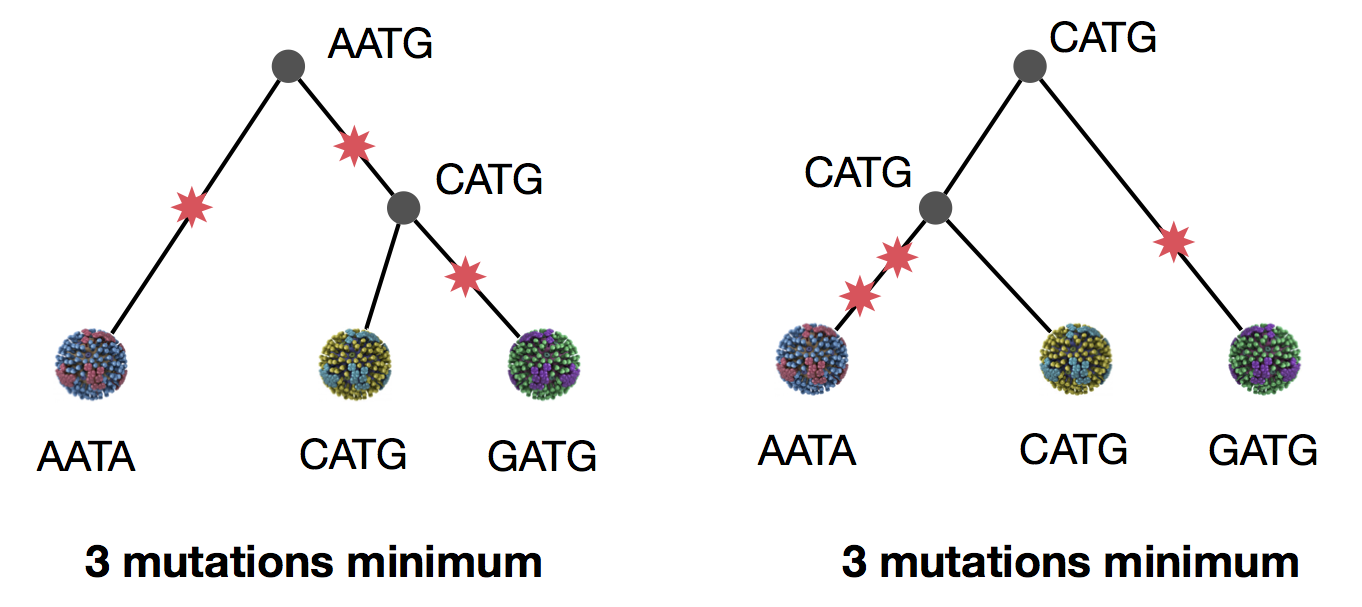
Parsimony suggests this topology requires 3 mutations at minimum
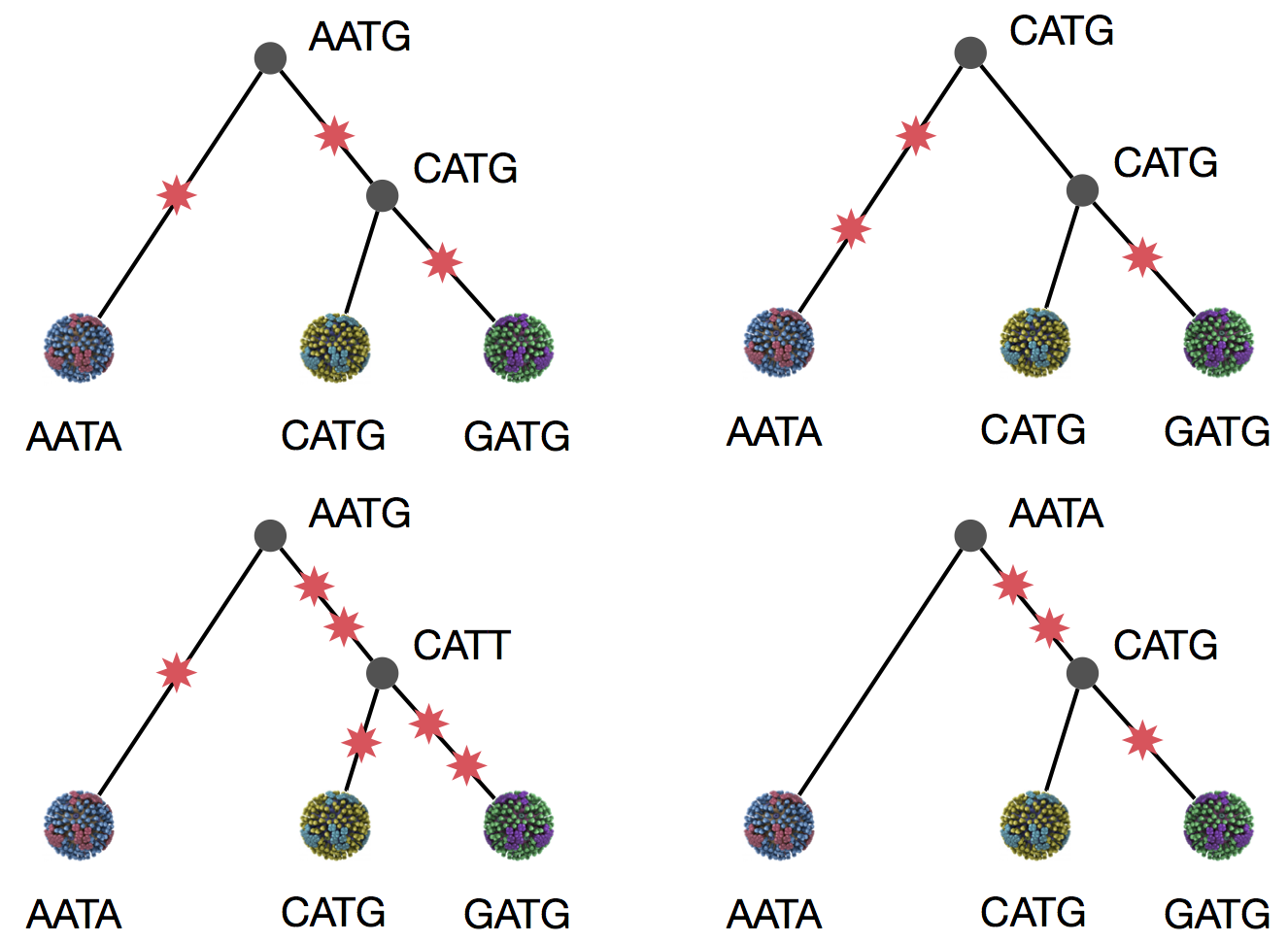
Parsimony suggests both topologies equally tenable
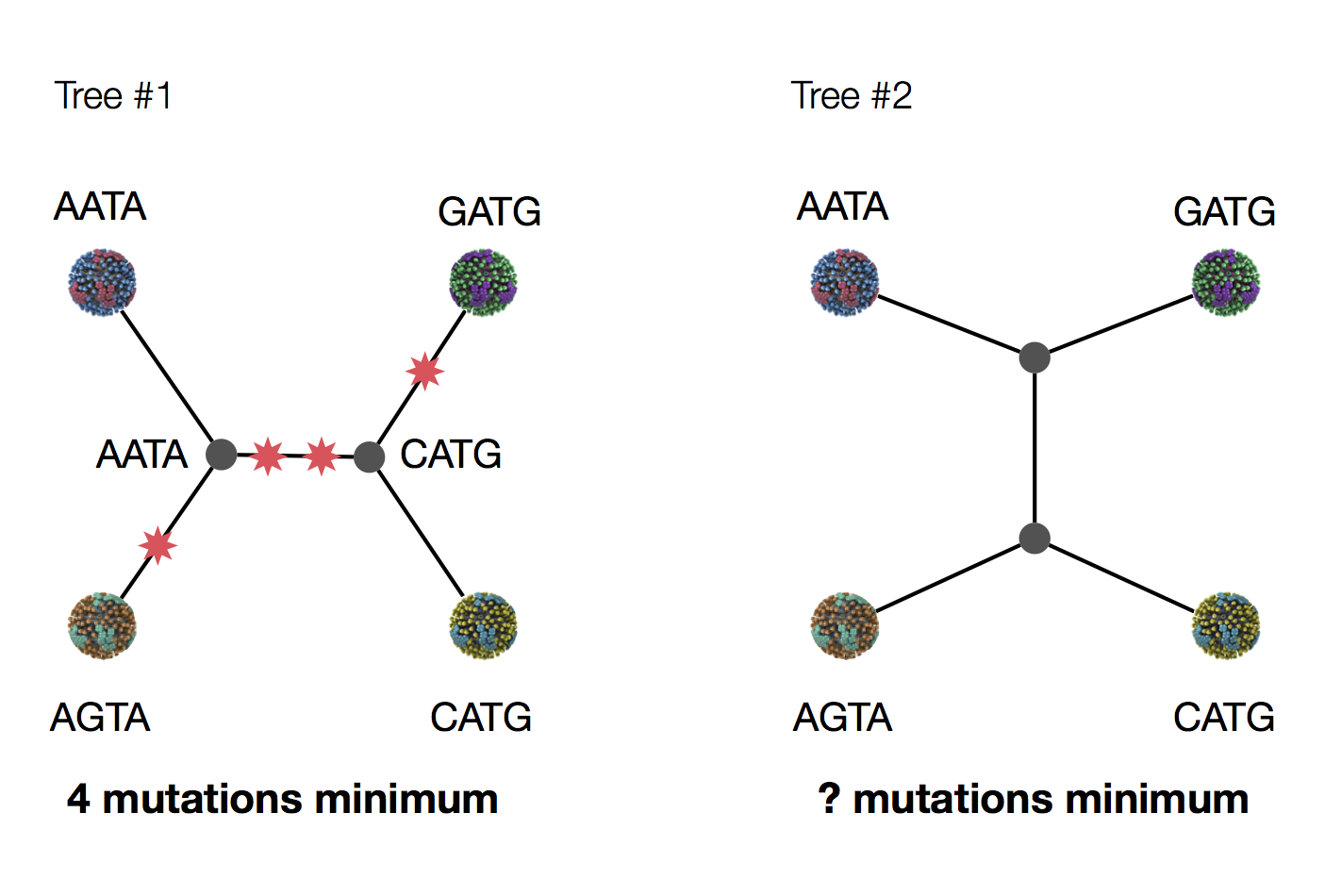
Exercise: which topology is more parsimonious?
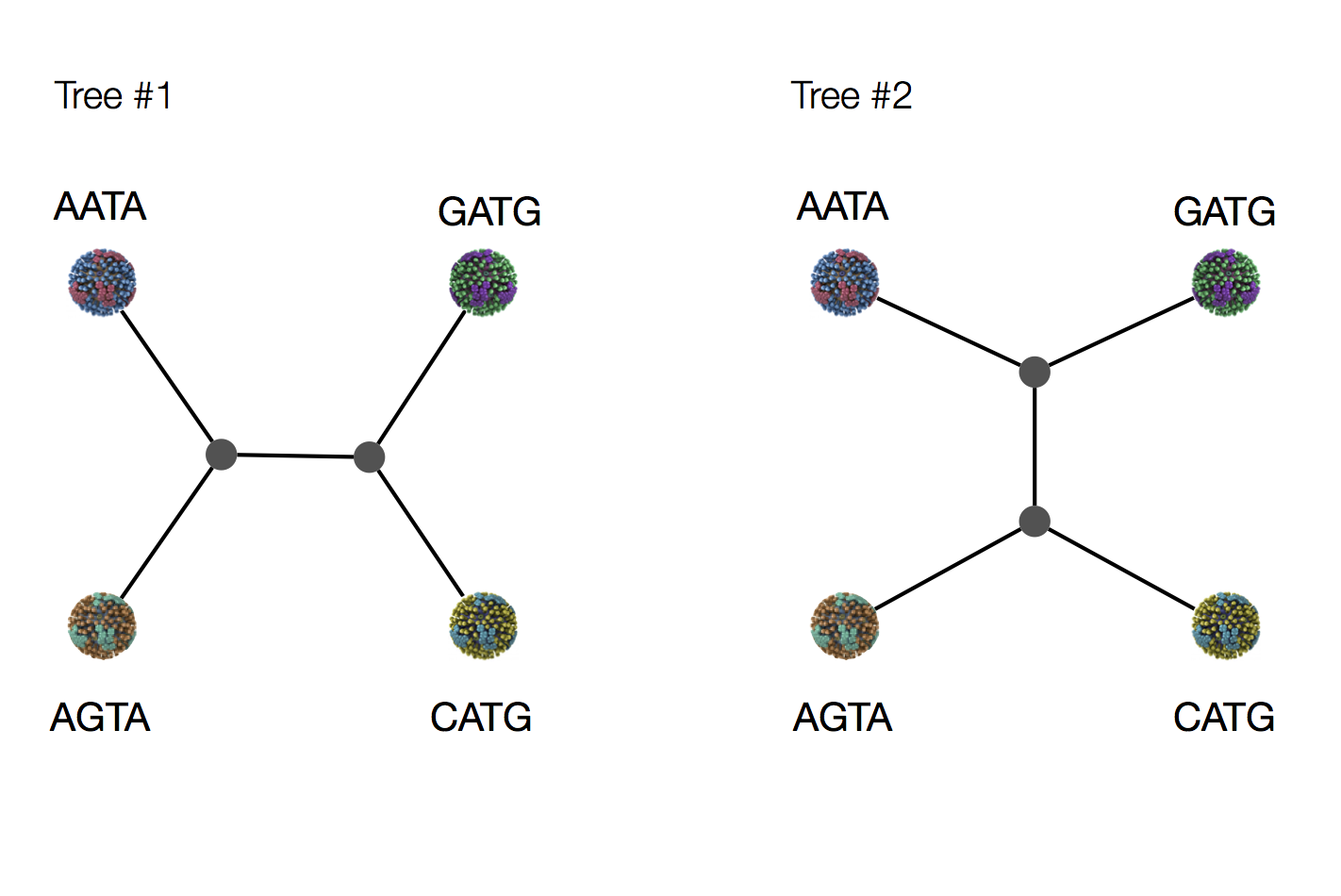
Exercise: which topology is more parsimonious?
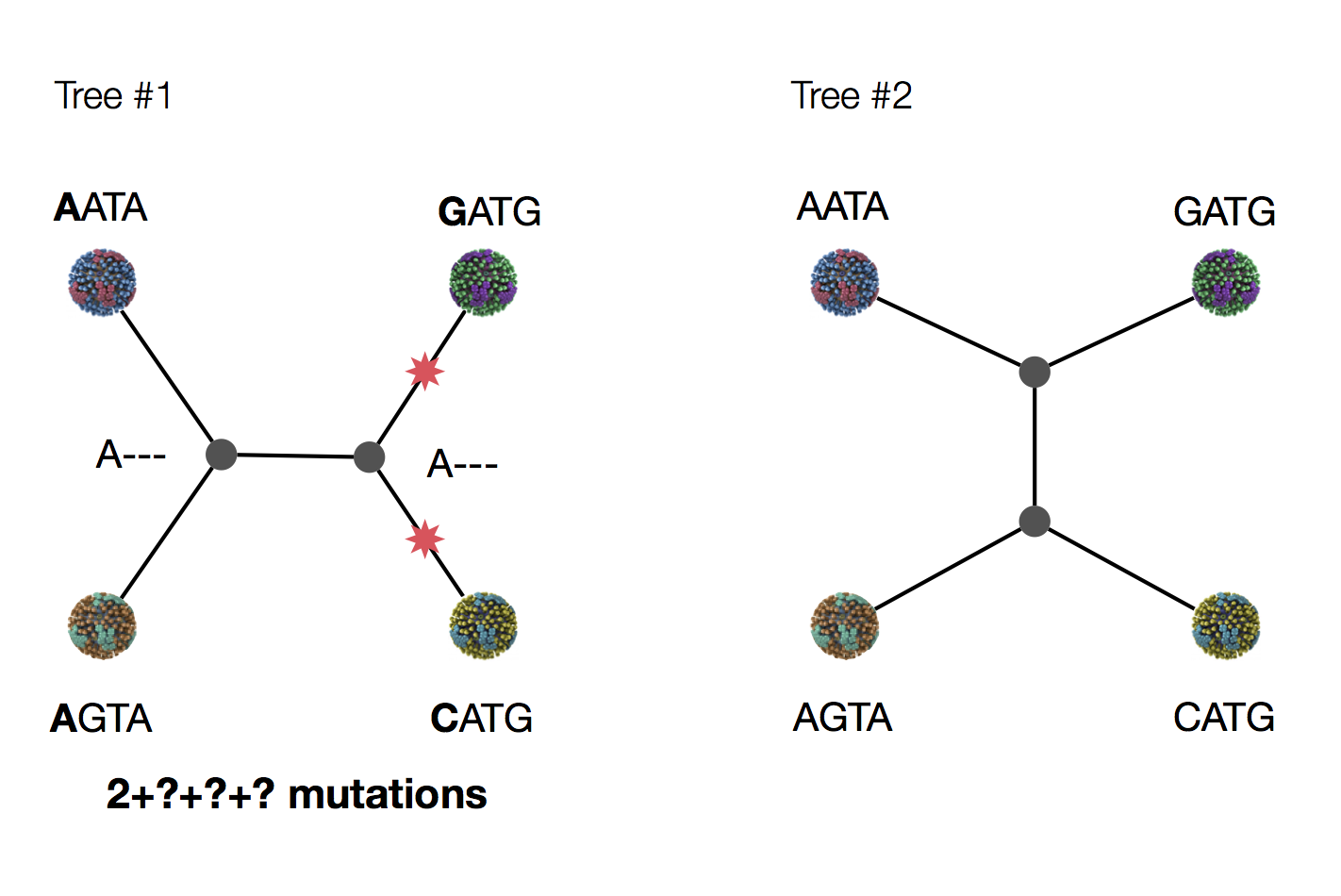
Exercise: which topology is more parsimonious?
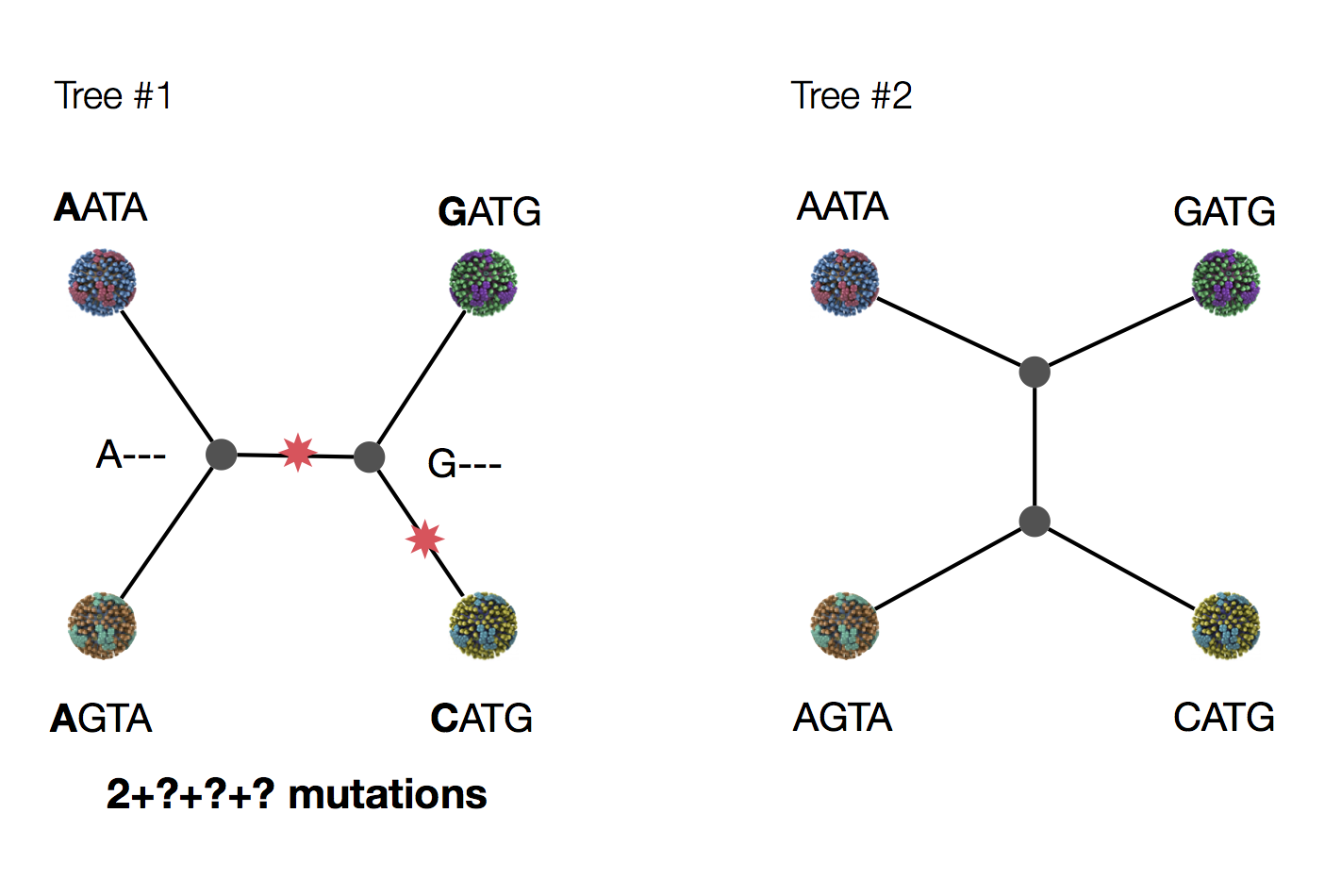
Exercise: which topology is more parsimonious?
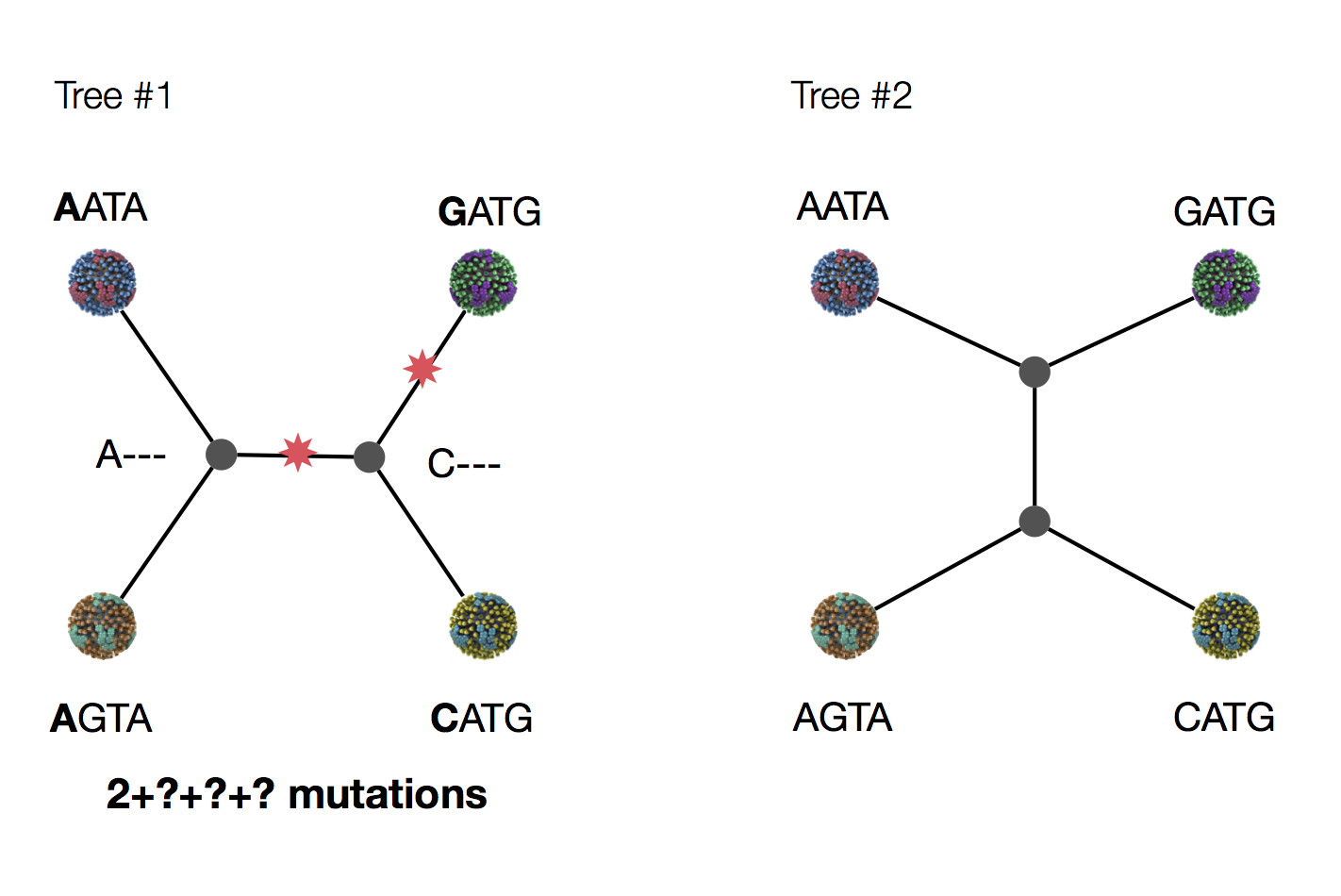
Exercise: which topology is more parsimonious?
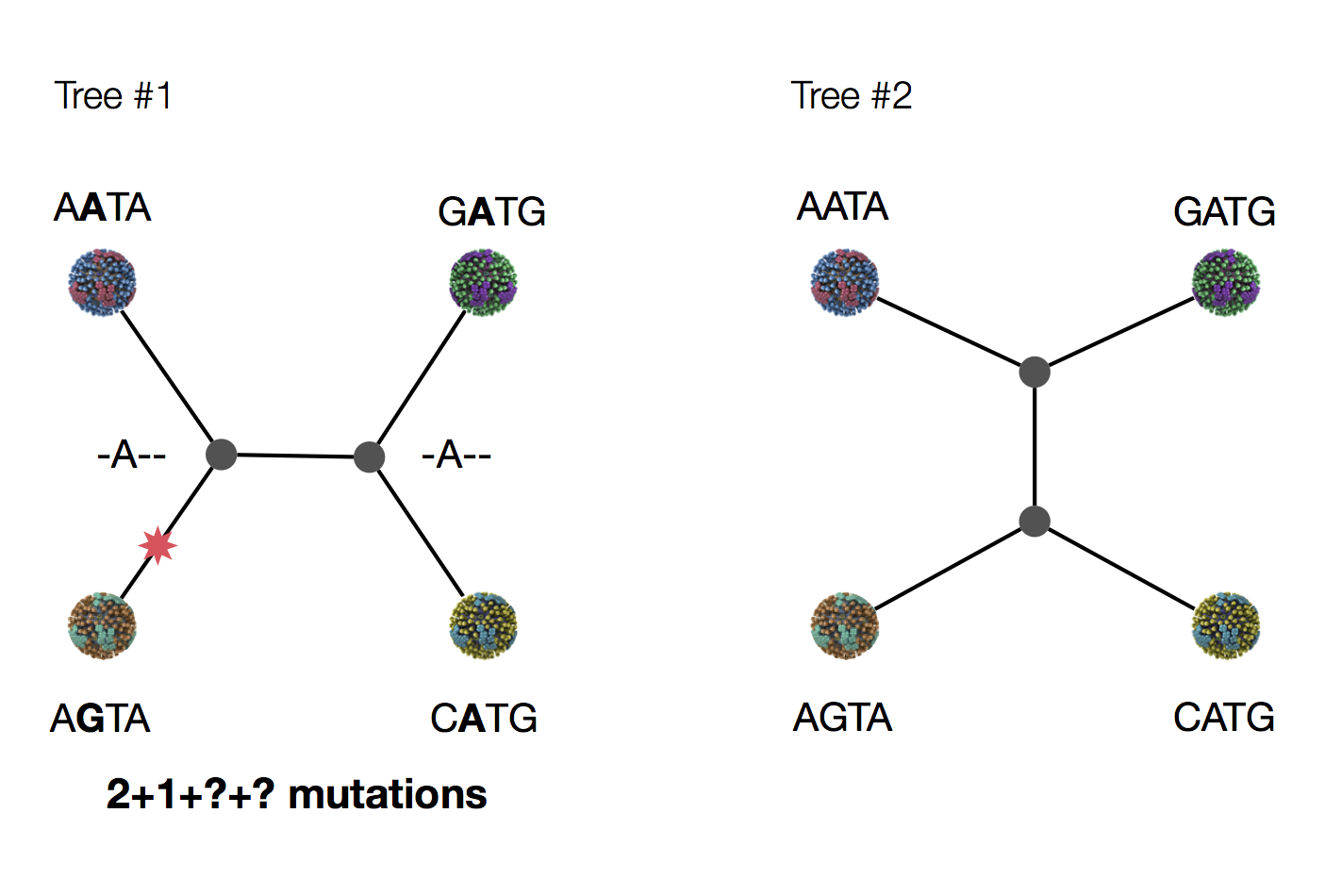
Exercise: which topology is more parsimonious?
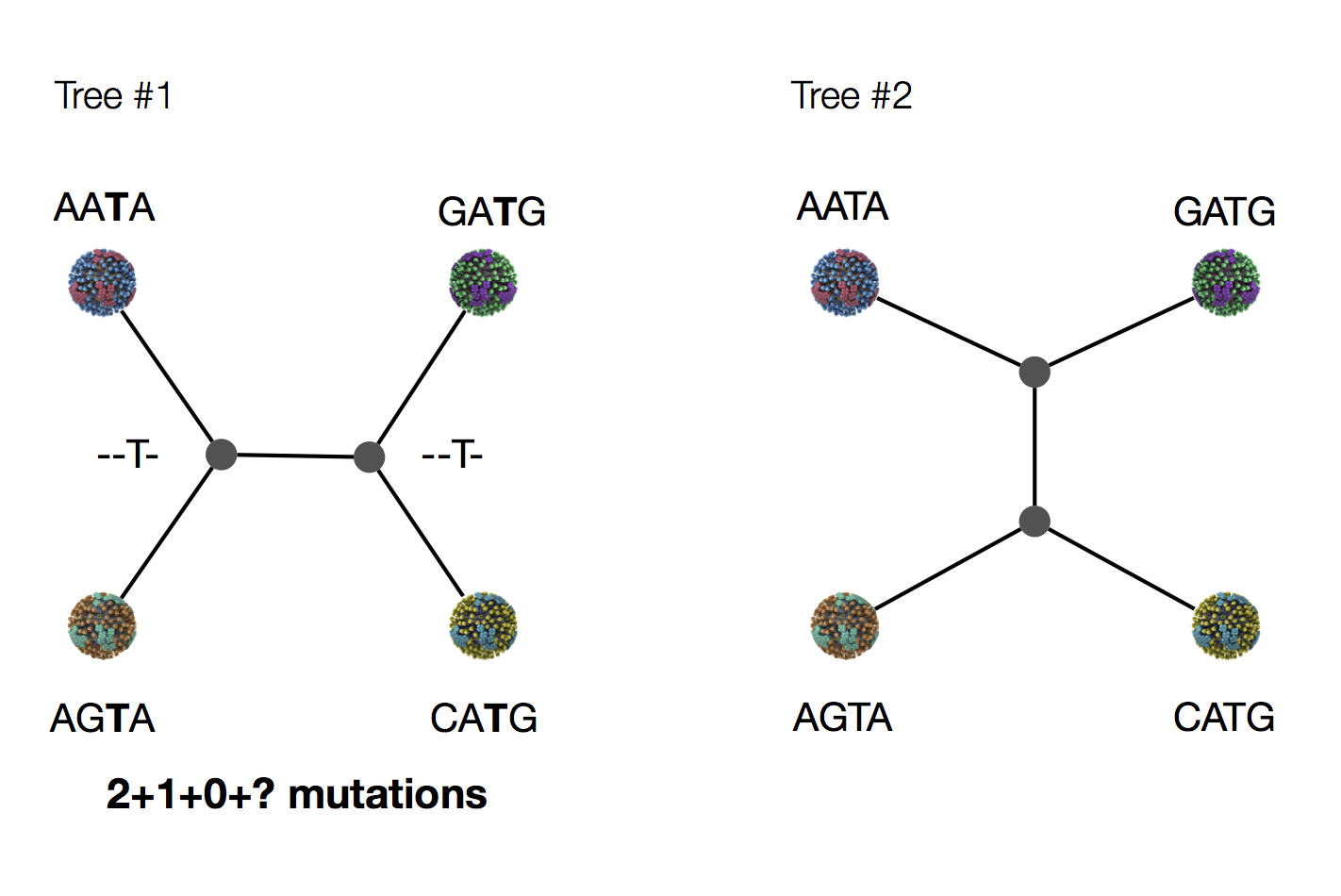
Exercise: which topology is more parsimonious?
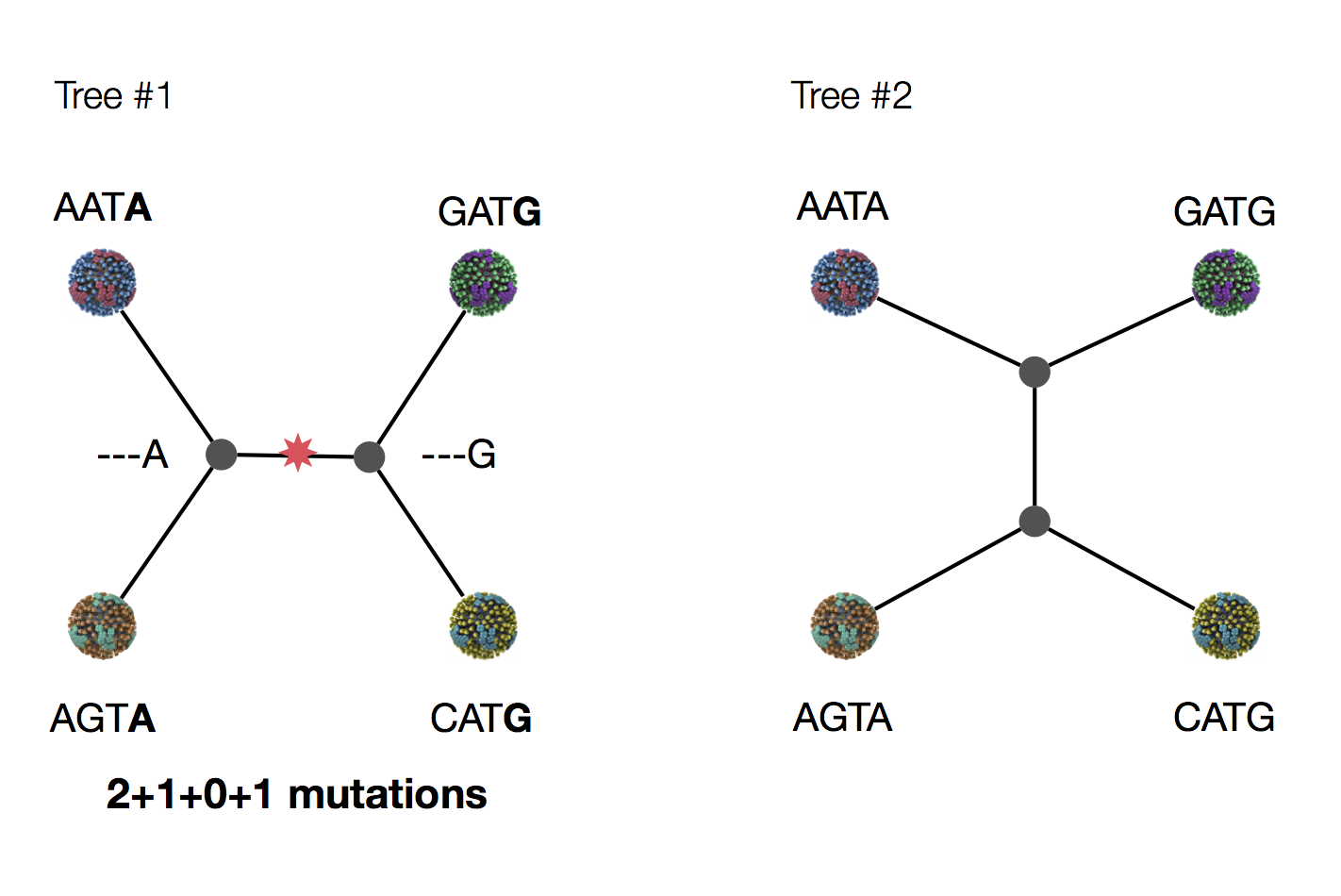
Exercise: which topology is more parsimonious?
Likelihood setup
- Come up with a statistical model of experiment
- Parametrize that model
- Evaluate likelihood under various parameter values
Example: flipping coins
Say that, after flipping a coin 20 times, we get 6 heads.
Model using the binomial distribution. Say \(p\) is the probability of getting a tail, and each draw is independent.
The likelihood of getting the observed result is \[ { {20} \choose 6} \, p^6 \, (1-p)^{20-6}. \] Recall: \({ {20} \choose 6}\) is the number of ways of choosing 6 items out of 20.
Exercise: likelihood surface
- Run
Beta_binomial.Rin R - Change the number of heads and tails.
- The maximum likelihood estimate of the parameter of interest is the parameter value(s) that maximize the likelihood. Here it's marked with a dot.
- What do you notice about the ML value when the observations are rare?
- How does the shape of the likelihood surface change when we get more observations?
Likelihood recap
- Maximum likelihood is a way of inferring unknown parameters
- To apply likelihood, we need a model of the system under investigation
- In general, the “likelihood” is the likelihood of generating the data under the given parameters, written \(P(D | \theta),\) where \(D\) is the data and \(\theta\) are the parameters.
Setup for likelihood based phylogenetics
The phylogenetic likelihood of a tree is the likelihood of generating the observed data given that tree (under the sequence evolution model).
Note that the UW’s own Joe Felsenstein was the first to formalize this and develop efficient algorithms.
Sequence evolution models tell us the probability of seeing a certain mutation in some period of (evolutionary) time
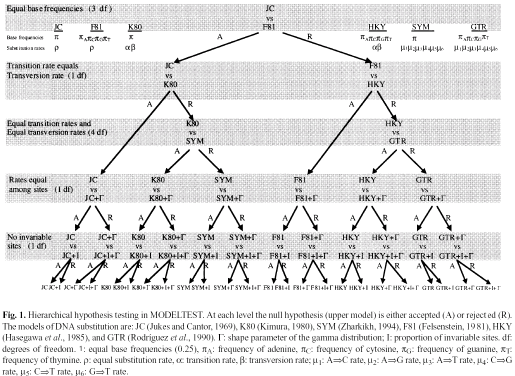
Model hierarchy, from Posada and Crandall
Calculating likelihood of a single column
Likelihood of an alignment
The phylogenetic likelihood of a tree is the likelihood of generating the observed data given that tree (under the sequence evolution model)
- Maximum likelihood gives a point estimate
- Confidence is assessed using the bootstrap
- Lots of flexibility with models
Bayes is magic
\[ P(\theta \mid D) \propto P(D \mid \theta) P(\theta) \]
Exercise: the prior and the posterior
- Open
Beta_binomial.Ragain. - Return the number of heads and tails to zero, and click "Bayesian".
- Alpha and Beta are the parameters of the prior. Try changing them around.
- Make them such that the prior is peaked around 0.5.
- Now, what happens when you vary the number of heads and tails?
The posterior probability of a tree is the probability that the observed tree is correct (given the model and priors)
- Bayesians sample from this posterior
- If you can deal with a prior, it’s the statistically right thing to do
- Sometimes we aren’t actually interested in the tree, so we can integrate it out
- But! Short alignment, 100 taxa = hours
Markov chain Monte Carlo
Metropolis-Hastings algorithm
- If you jump to a better tree, accept that move
- If you jump to a worse tree, accept that move with a non-zero probability
- It’s all arranged so that you sample trees in proportion to their posterior probability
Subset to high probability nodes
Real tree spaces have bottlenecks

Likelihood phylogenetics recap
- In likelihood phylogenetics, explicitly model mutation process
- This allows complex models to be used
- Statistical basis allows us to make formal statements about uncertainty
- But on the other hand our models are over-simple!
Crazy but typical model assumptions
- differences between sequences only appear by point mutation
- evolution happens on each column independently
- sequences are evolving according to reversible models (this excludes selection and directional evolution of base composition)
- the evolutionary process is identical on all branches of the tree
To read
- Inferring Phylogenies by Felsenstein
- The phylogenetic handbook edited by Lemey, Salemi, and Vandamme, chapters by the stars
- Bodega phylogenetics tutorials