Multistrain models

In multistrain models, pathogens (or immune cells) interact via resource competition

Infection by strain $i$ creates immunity to strain $i$, but also to strain $j$

Consuming antigen $i$ by clone $x$ depletes antigen $i$ for consumption by clone $y$

Simple SIR model

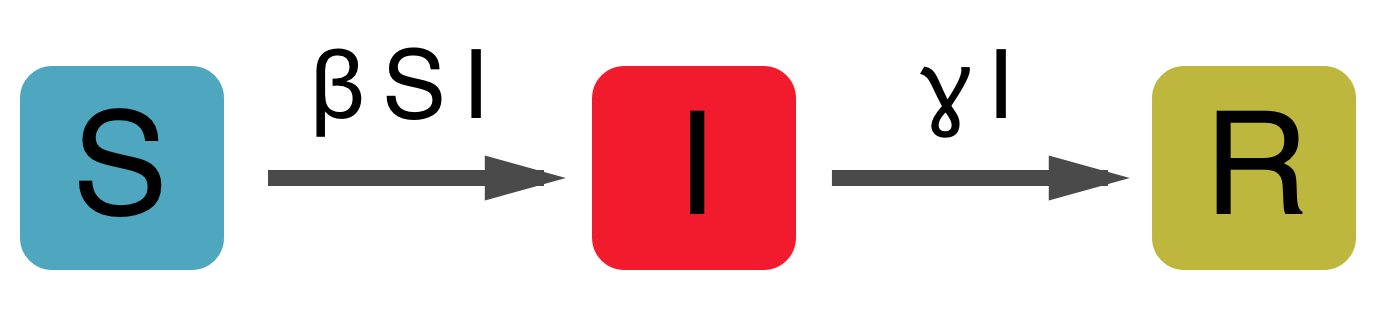
$dS/dt = - \beta S I$

$dI/dt = \beta S I - \gamma I$

$dR/dt = \gamma I$

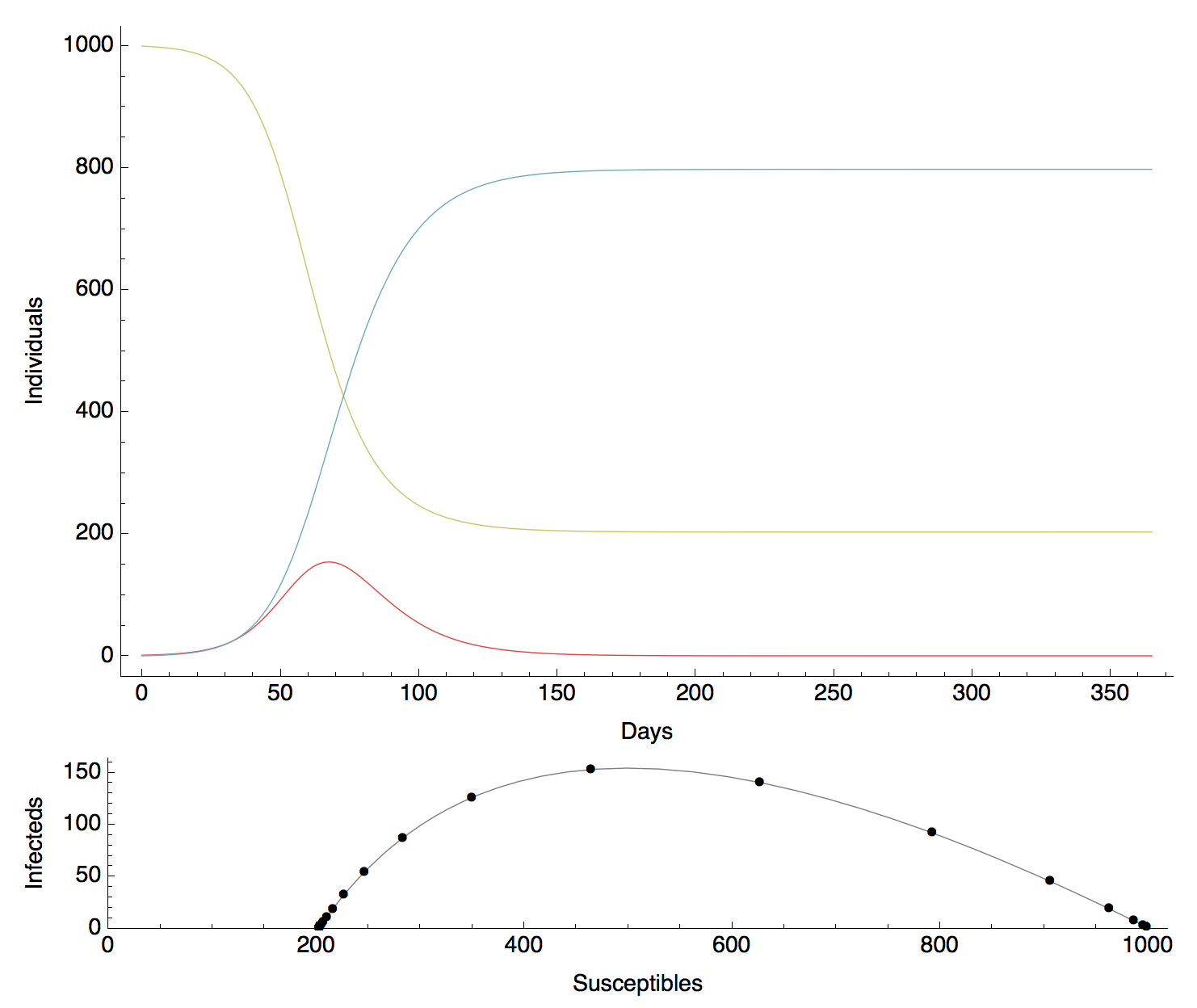
Simple SIR behavior

SIR model with vital dynamics

$dS/dt = \mu - \beta S I - \mu S$

$dI/dt = \beta S I - \gamma I - \mu I$

$dR/dt = \gamma I - \mu R$

Fundamental reproductive number

Growth when 100% of population is susceptible

$$dI/dt = \beta S I - \gamma I - \mu I = \beta I - \gamma I - \mu I = (\beta - \gamma - \mu) I$$

$$R_0 = \frac{\beta}{\gamma + \mu}$$

SIR with vital dynamics behavior

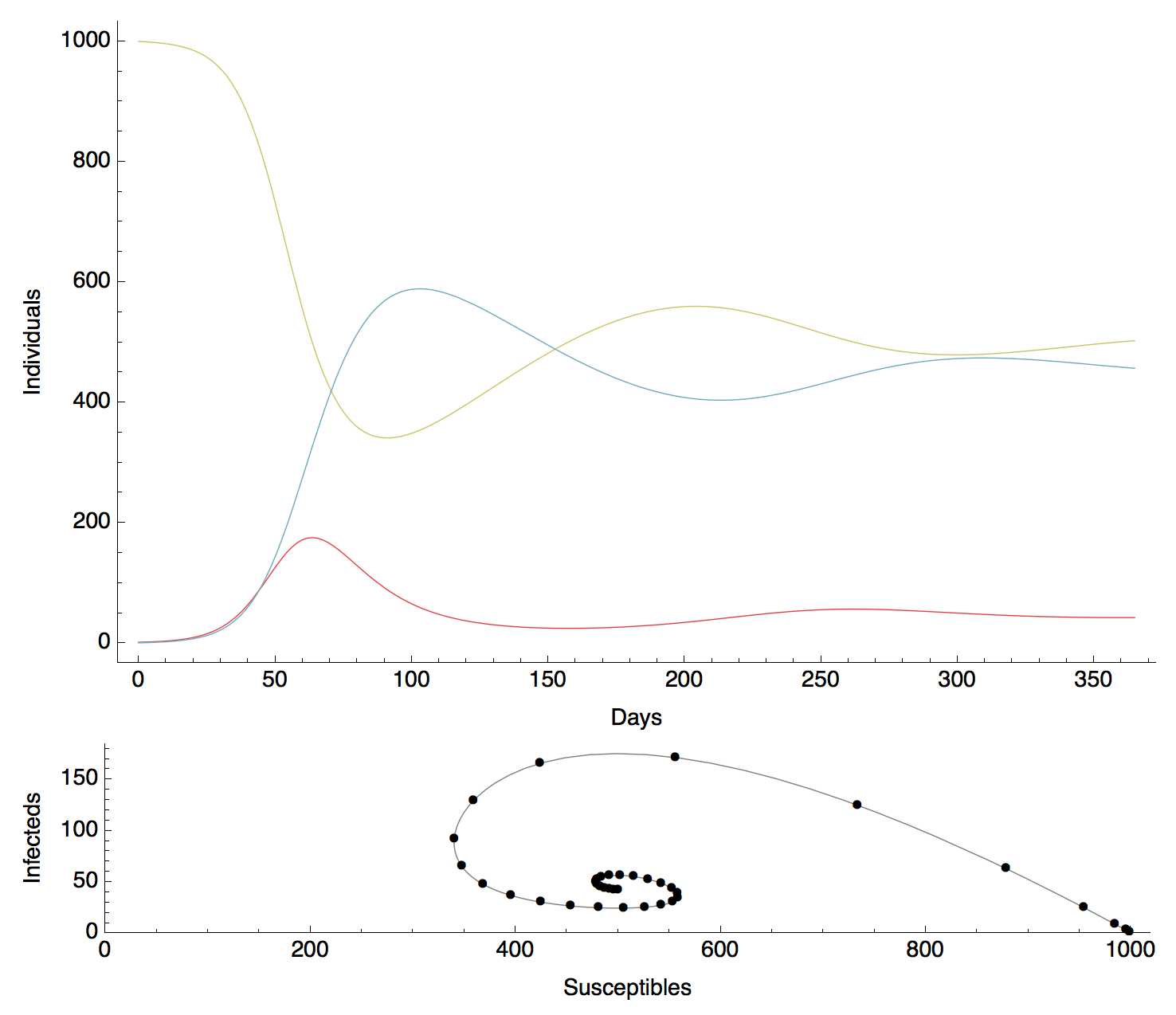
Solving for endemic equilibrium

Equilibrium when $S$, $I$ and $R$ remain constant through time

$$dI/dt = 0 = \beta S^* I^* - \gamma I^* - \mu I^*$$

$$\beta S^* I^* = \gamma I^* + \mu I^*$$

$$\beta S^* = \gamma + \mu$$

$$S^* = \frac{\gamma + \mu}{\beta} = \frac{1}{R_0}$$

With this equation, we can solve for equilibrium infecteds

$$I^* = \frac{\mu}{\beta} (R_0 - 1)$$

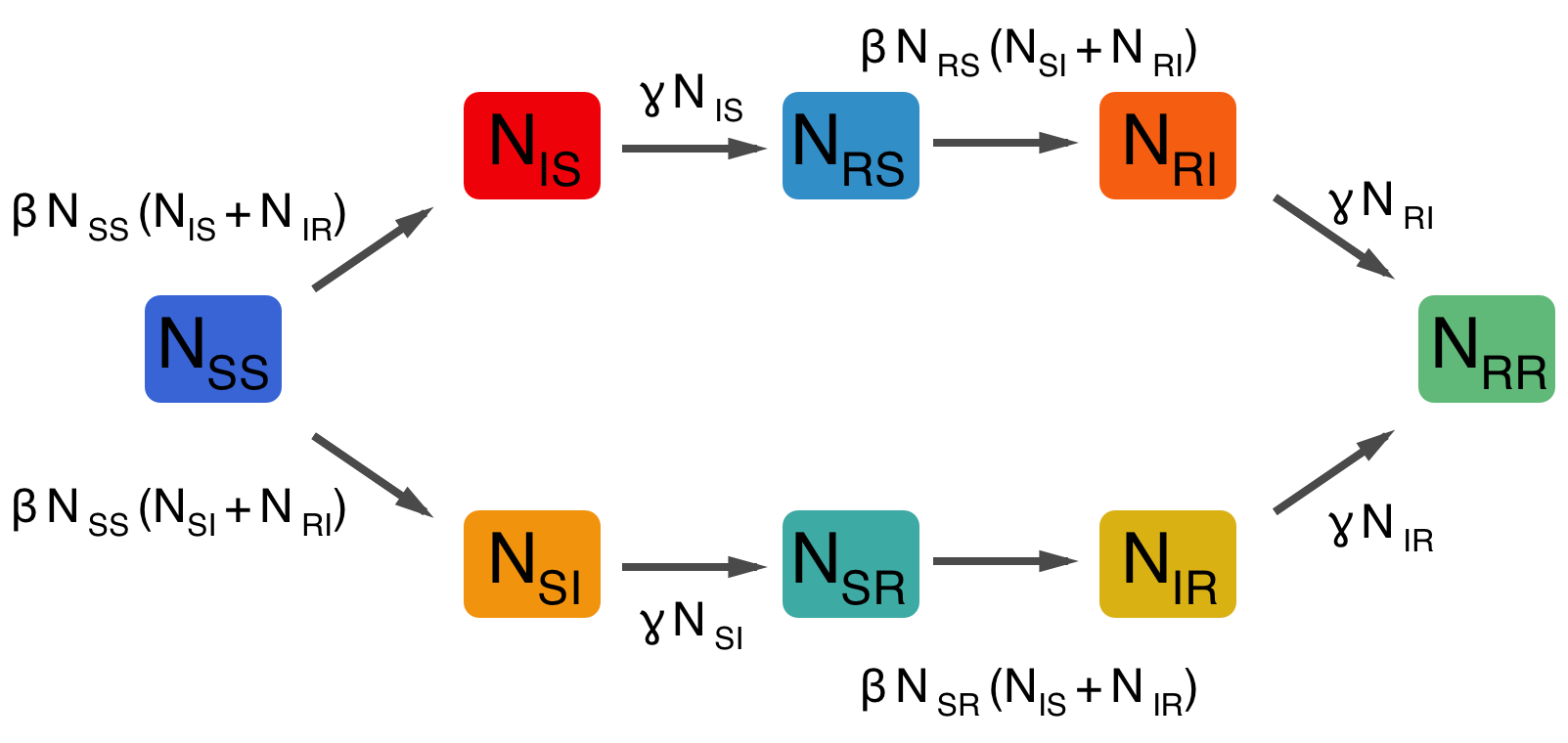
Two-strain SIR model, independence between strains

All the following have host birth/death arrows omitted for clarity

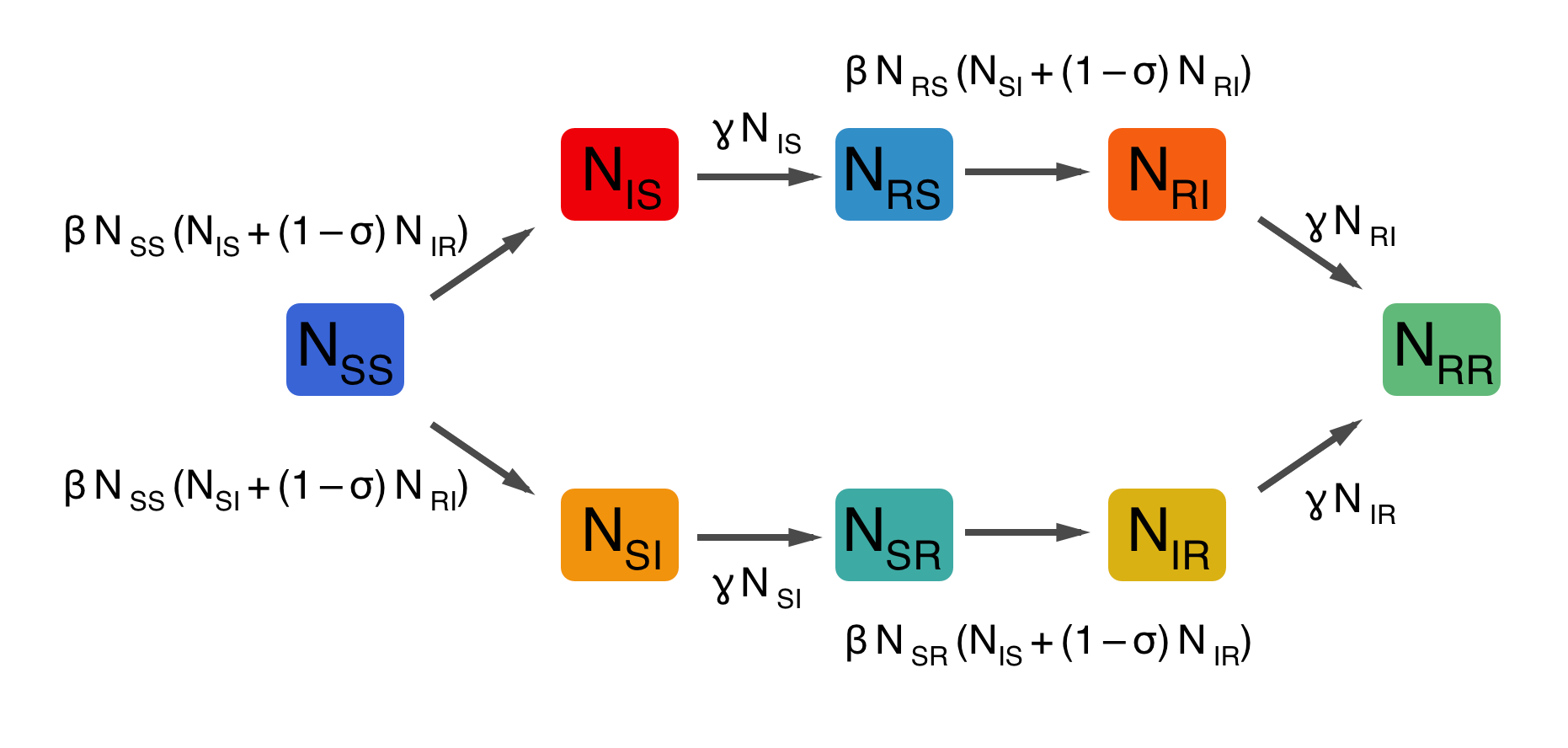
Two-strain SIR model, cross-immunity mediated through transmission

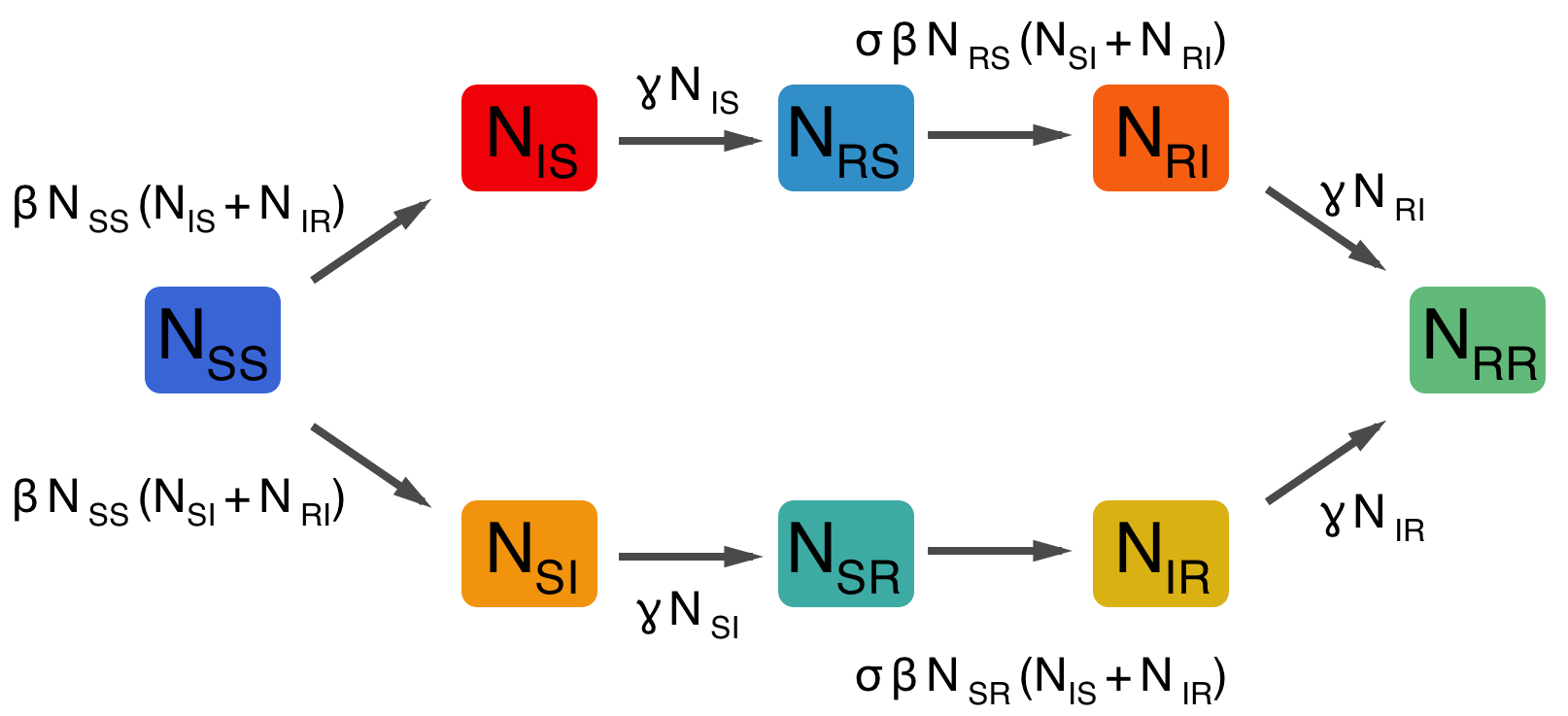
Two-strain SIR model, cross-immunity mediated through susceptibility

Variety of ways to parameterize interactions

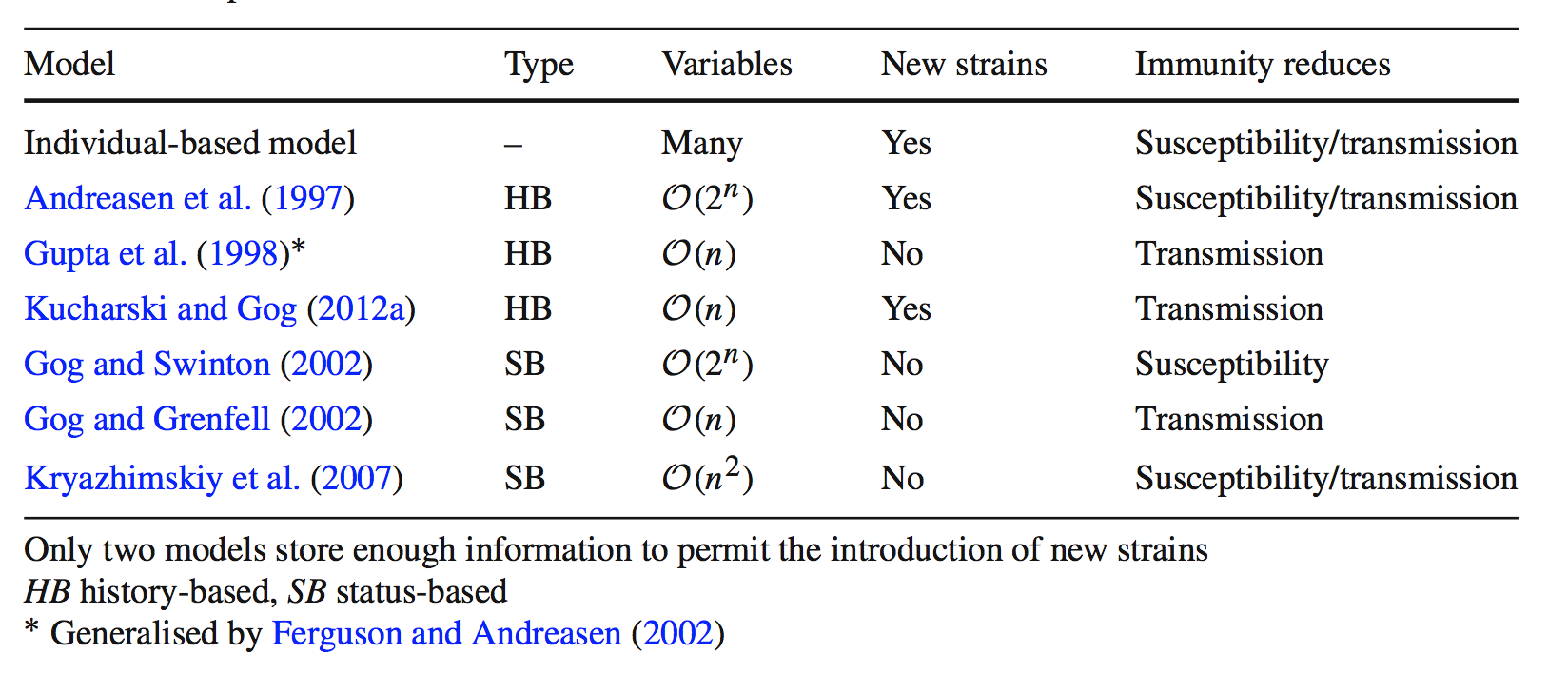
Two-strain SIR model, cross-immunity through polarizing immunity

Exercise: invasion of second strain into an endemic population

Assuming the model of polarizing immunity, allow a single strain to reach endemic equilibrium

$$S^*_1 = \frac{1}{R_0}, I^*_1 = \frac{\mu}{\beta} (R_0 - 1)$$

After strain 1 equilibrium is reached, allow strain 2 to enter the population. Strains share $R_0, \beta, \gamma, \mu$ parameters.

Questions: What is the endemic equilibrium $S^*_2$ for strain 2? Given $S^*_2$, what is the initial growth rate of strain 2? What effect does $\sigma$ have on this growth rate? When can strain 2 invade?

Dynamical outcomes of invasion

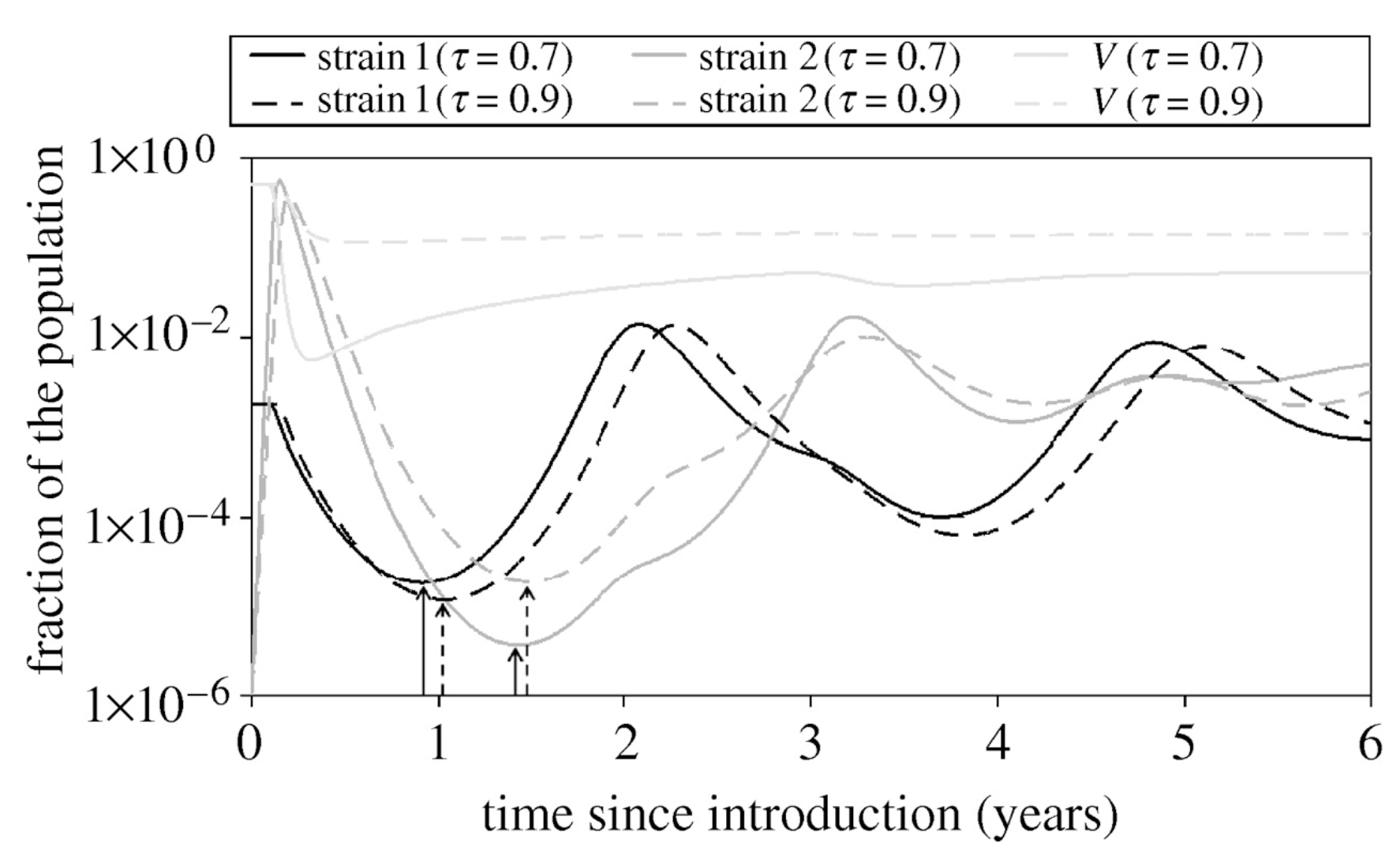
Dynamical outcomes of invasion

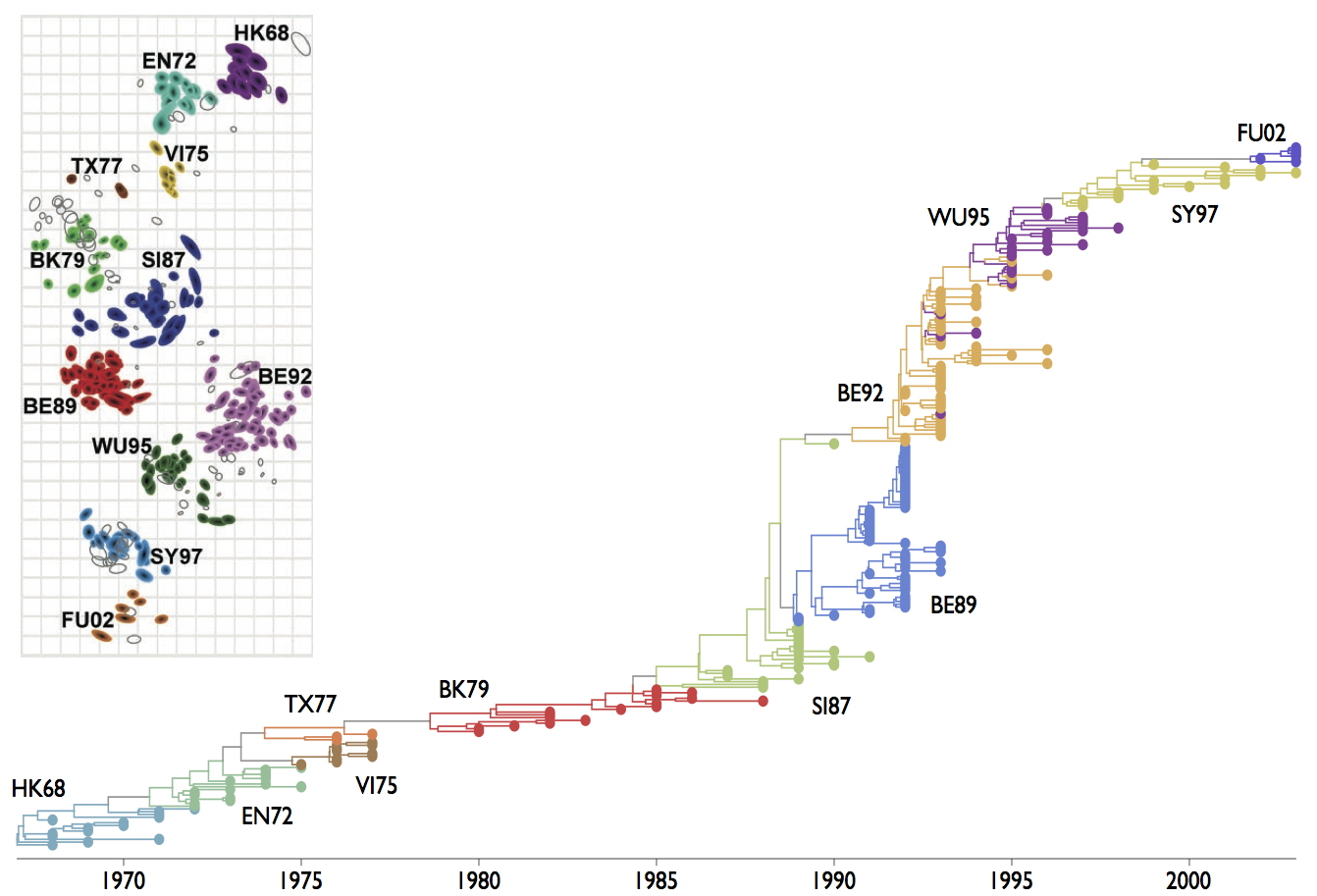
Under some regimes, may result in continual strain turnover

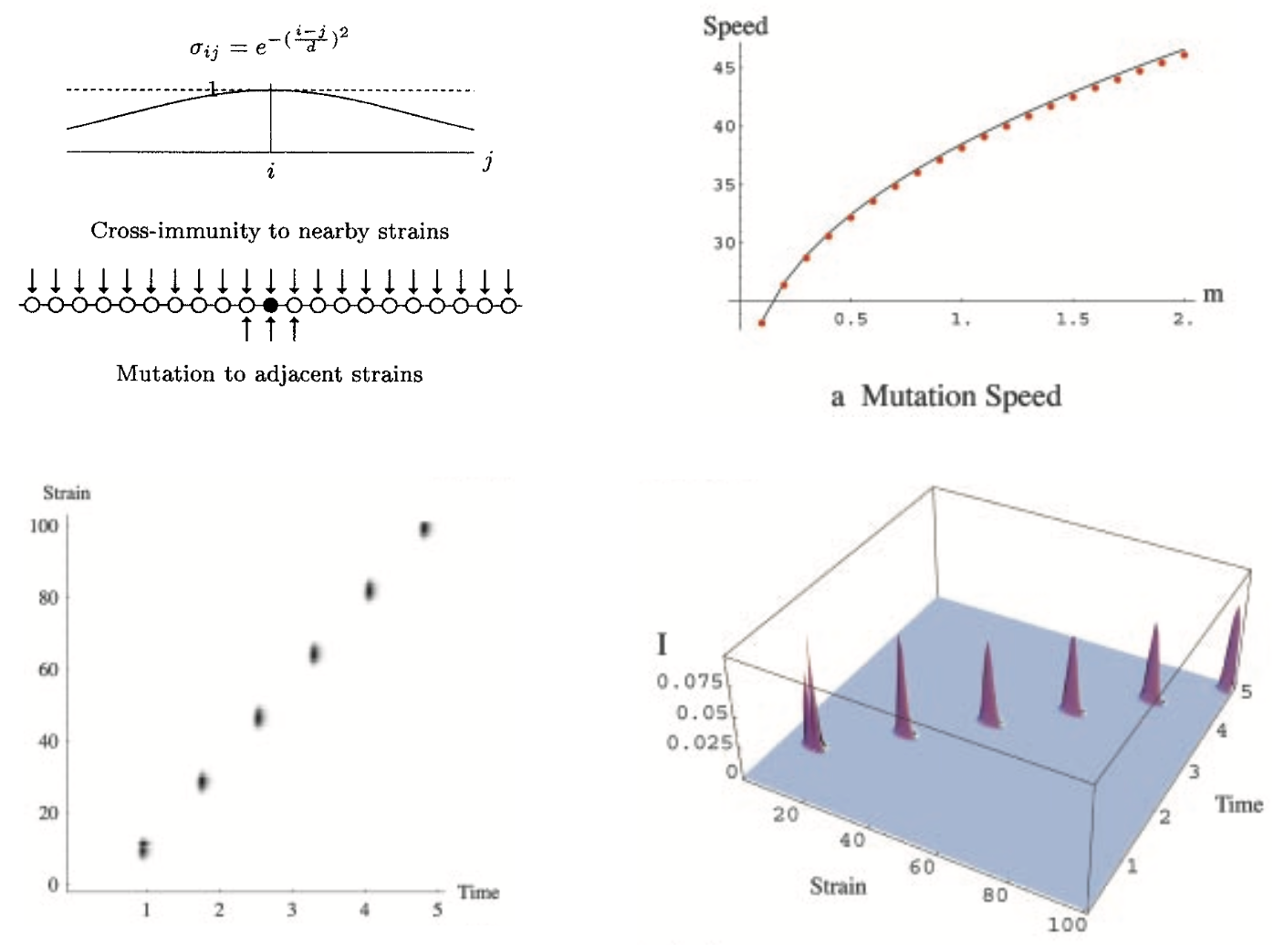
Again, looks similar to strain replacement in influenza