Selection and evolution in B cells



Most slides from Sarah Cobey ; some from Erick

B cells determine antibody diversity

Murphy 2011

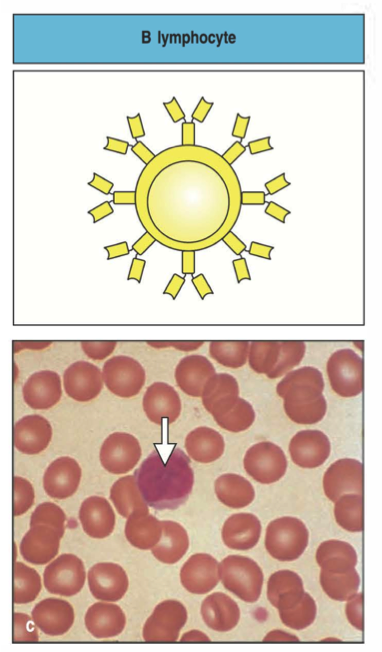
Structure of a B cell receptor

Georgiou et al. 2014

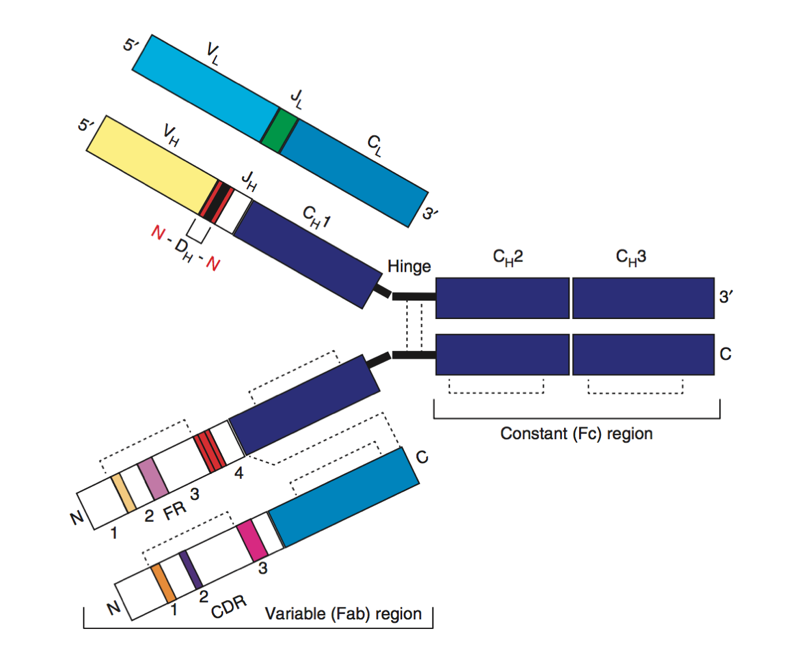
Origins of B cell receptor diversity

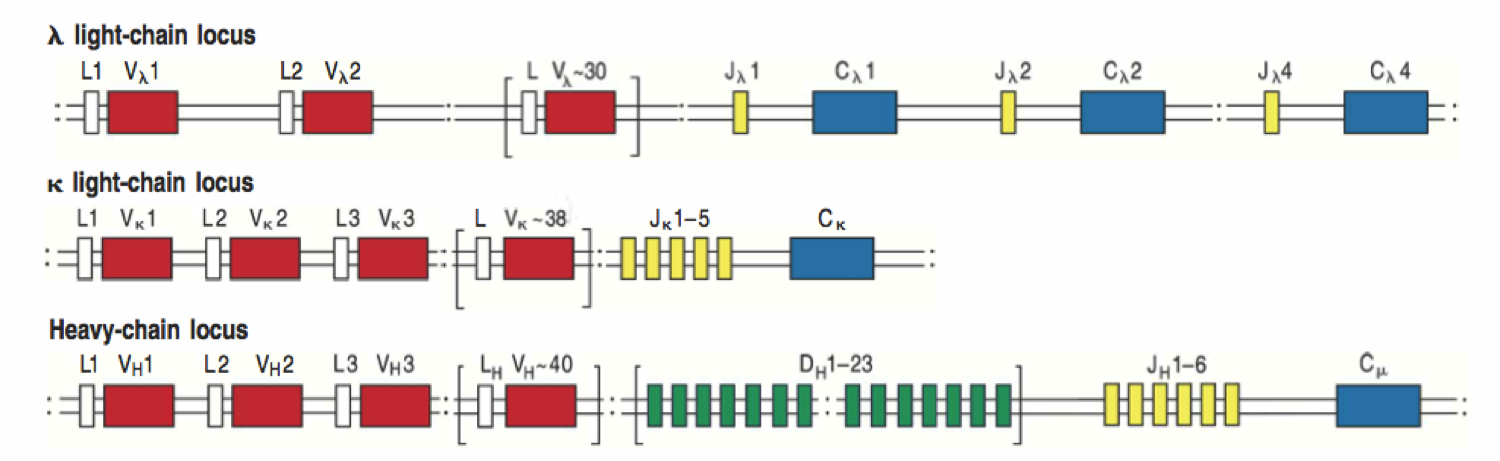
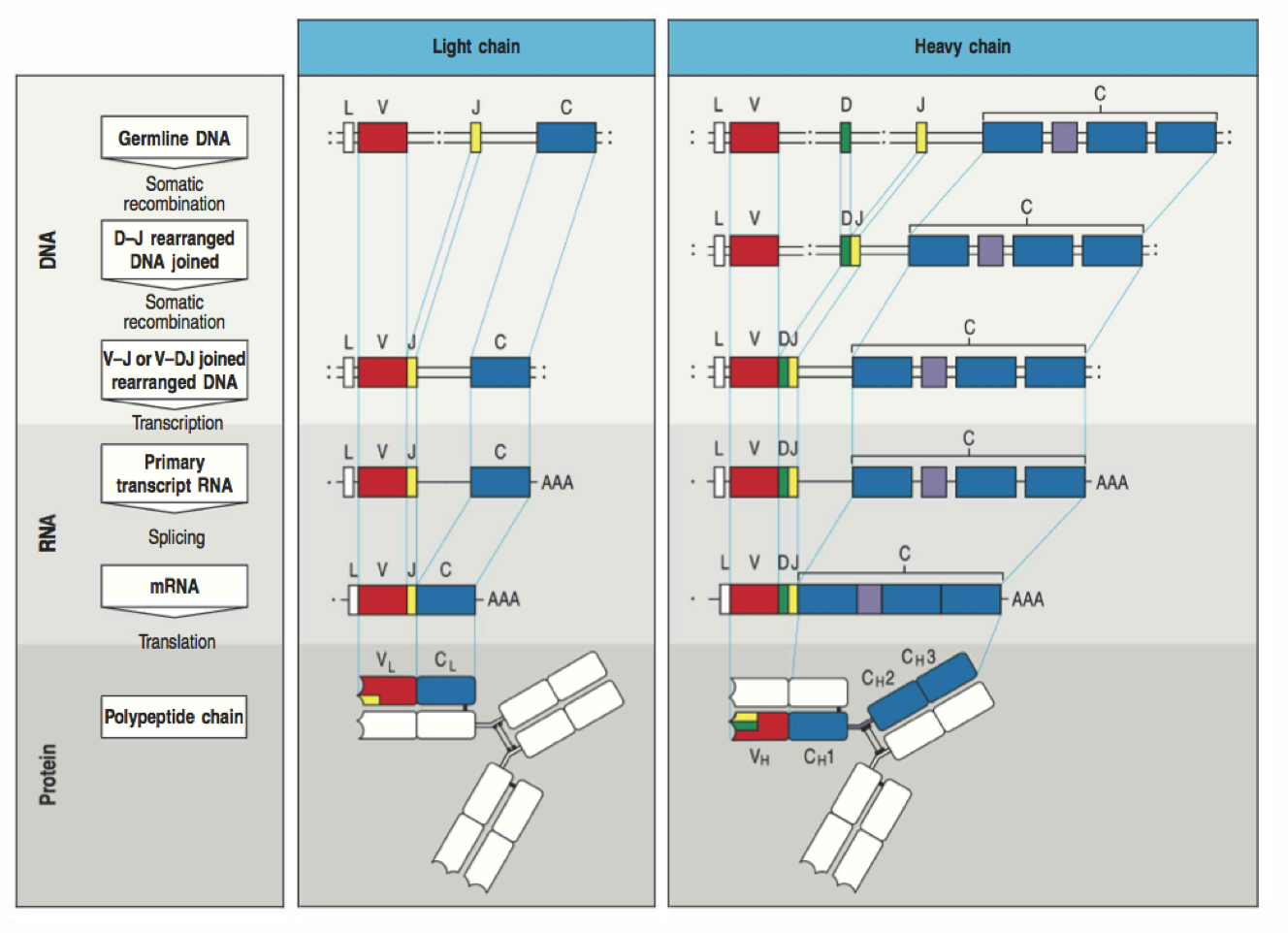
VDJ recombination

Affinity maturation

VDJ loci

Murphy 2011

VDJ recombination

Murphy 2011

Selection on naive repertoire

Stability

Autoreactivity

Tas et al. 2016

Somatic hypermutation is AID + repair

Teng and Papavasiliou 2007

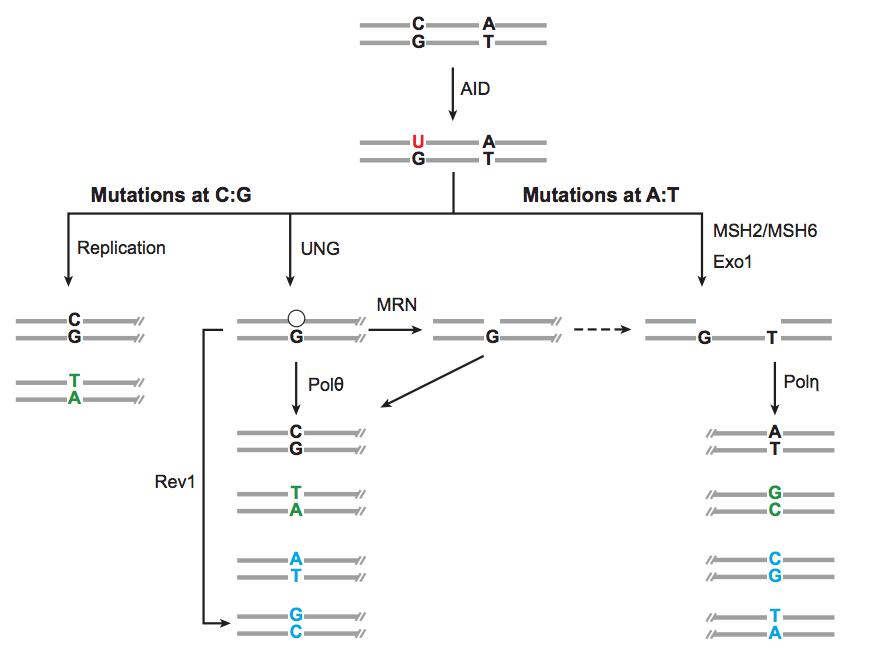
Mutation rate varies over BCR

Wei et al. 2015

The mutations have peculiar biases


The mutations have peculiar biases


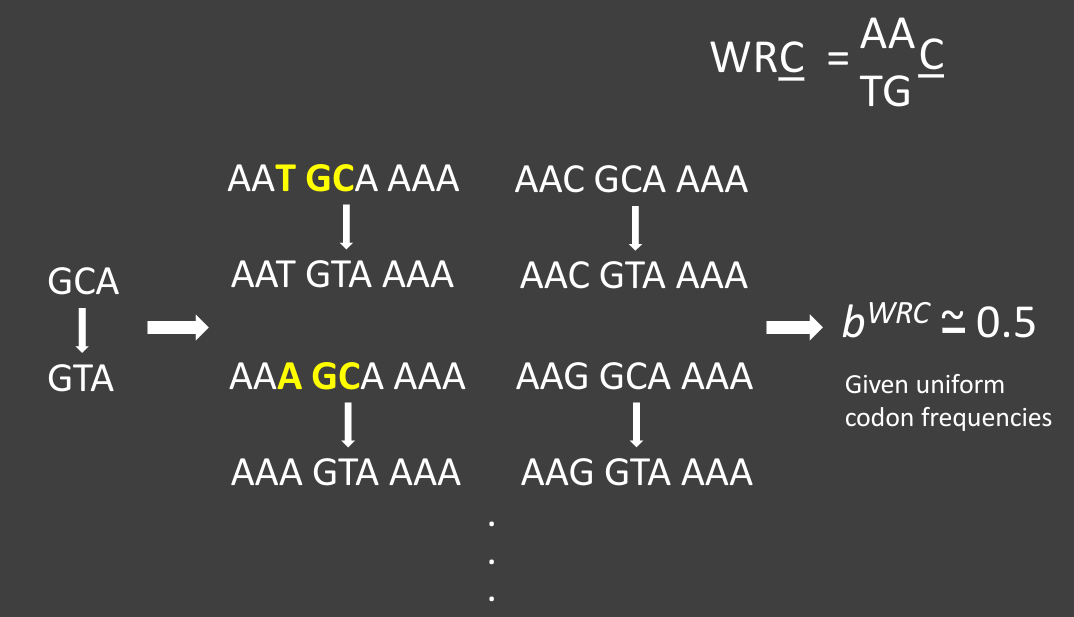
One would like to quantify these biases

Phylogenetics is not straightforward

Hoehn et al. 2017

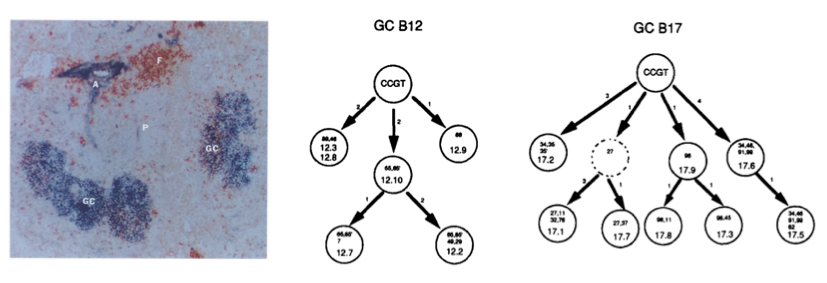
GC B cells evolve

Jacob and Kelsoe 1992

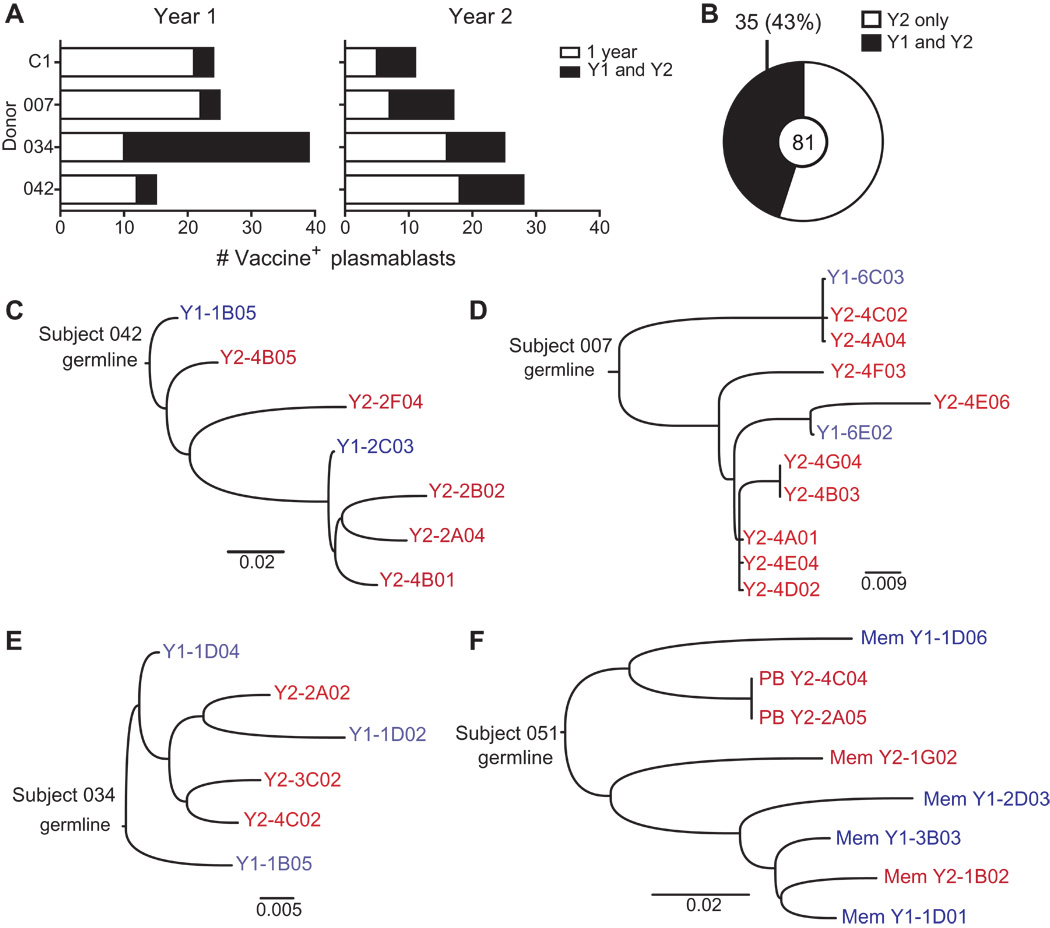
Permissive selection vs complex antigens

Kuraoka et al. 2016

Memory cells can affinity mature

Andrews et al. 2015

Antibody isotypes

Absolute Antibody

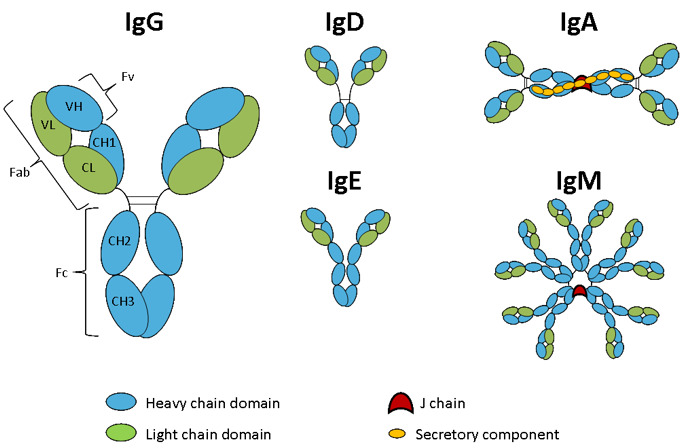
Isotype switching

Wikipedia

Clones can be long-lived

Liao et al. 2013

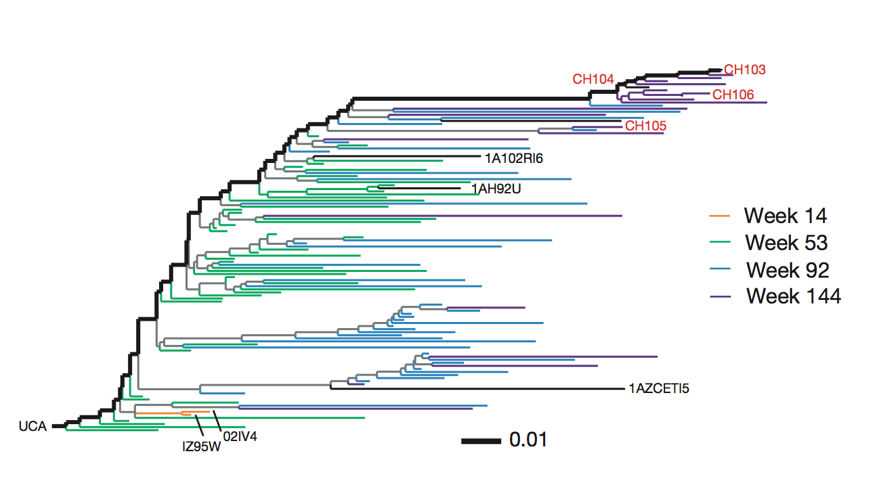
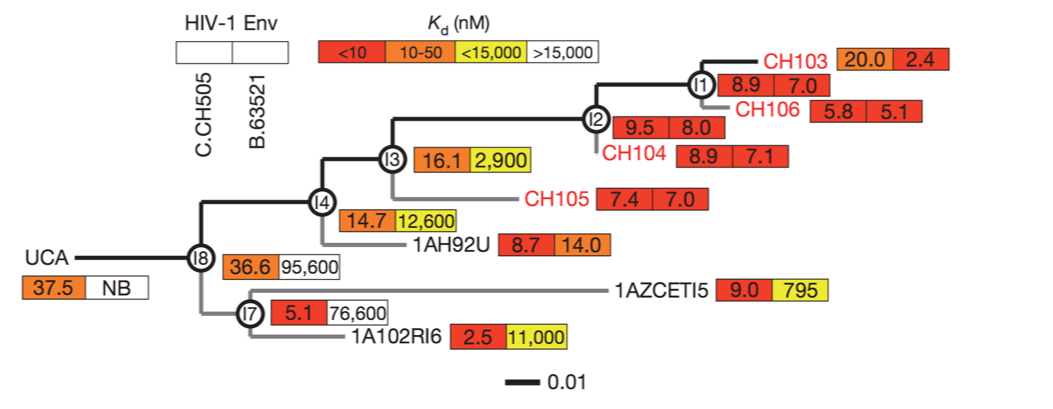
Broadly neutralizing antibodies are often highly diverged

Liao et al. 2013

Broadly neutralizing antibodies to flu elusive

Ekiert et al. 2011

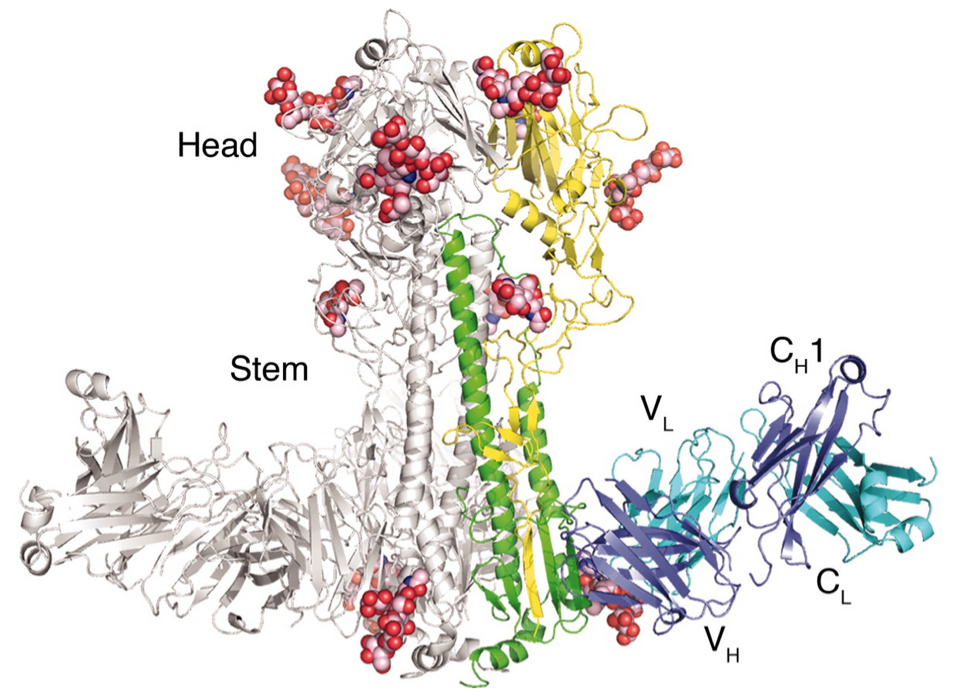
Why do some people develop broadly neutralizing antibodies?

Can we induce them in everyone?

Will they dominate?

"Restricted" responses to epitopes

Dunand and Wilson 2015

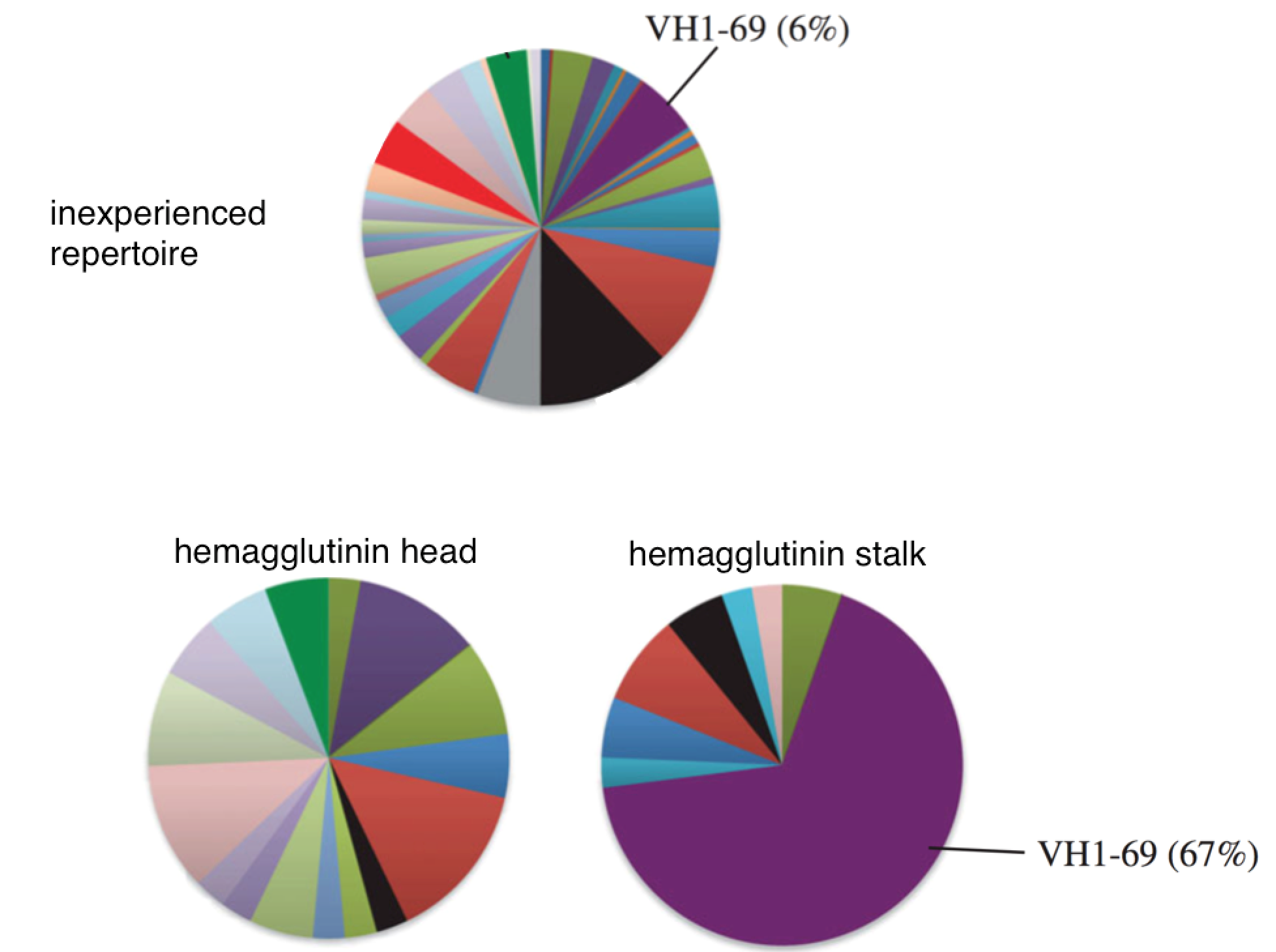
Genotype affects response to H5N1 vaccination

Avnir et al. 2016

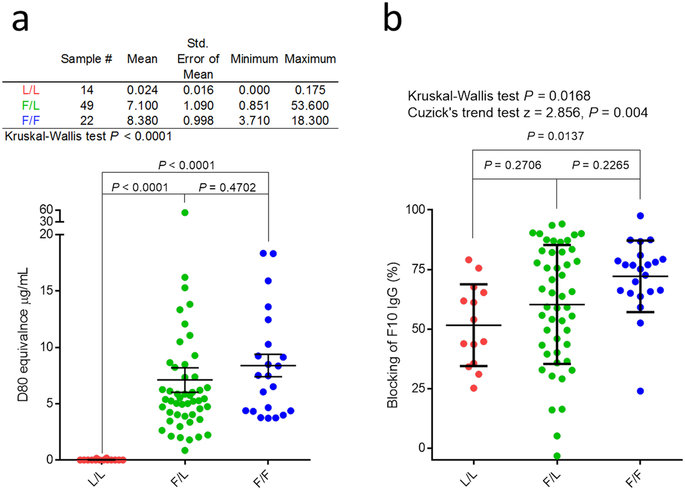
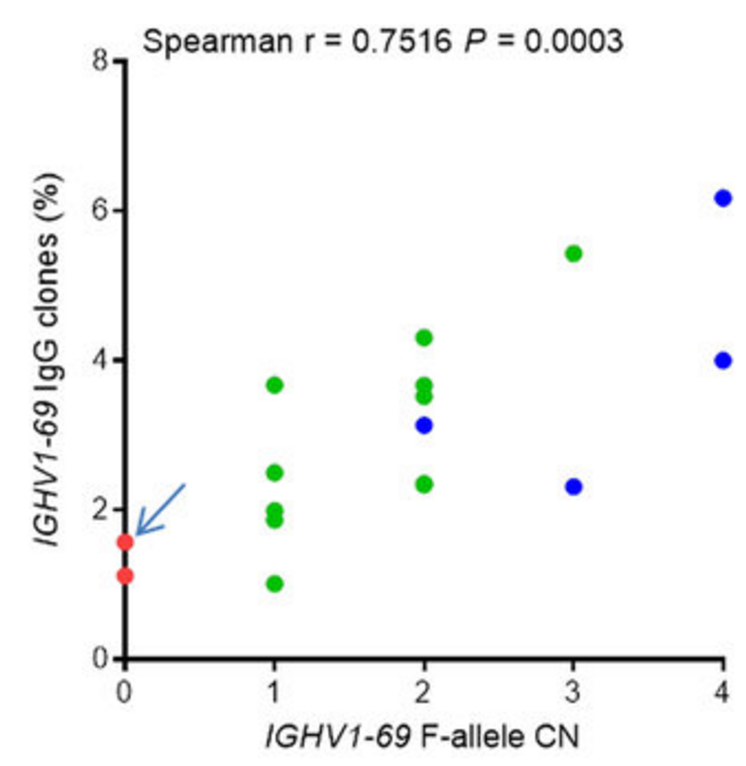
Allele copy number affects clone frequency

Avnir et al. 2016

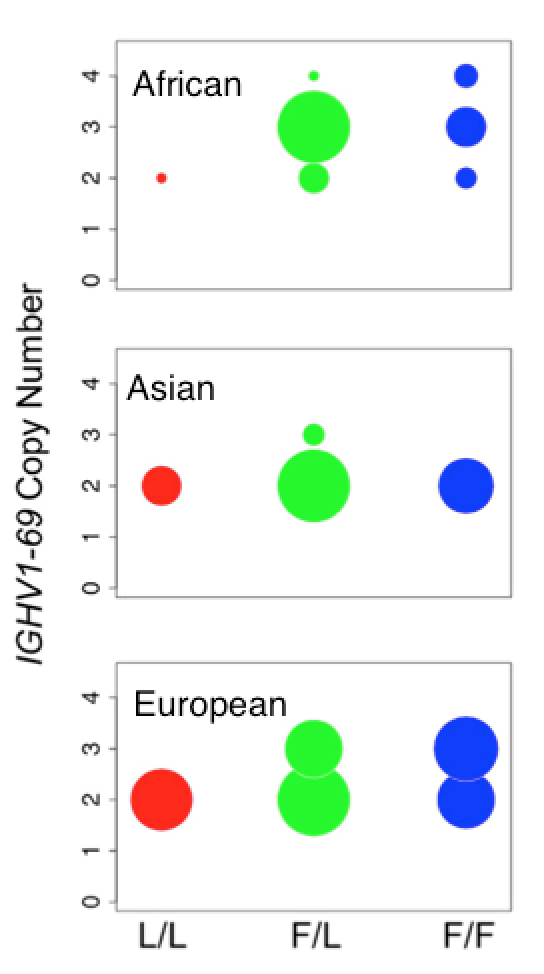
Ethnic differences in copy number

Avnir et al. 2016

How can we learn using probabilistic models?

We don’t need lots of little techniques…

we only need models and one principle: likelihood.

We can sequence BCRs in high throughput

How do we learn from BCR sequences?

  1. Develop probabilistic model of biological process and how data is generated.
  2. Find parameter choices that maximize the likelihood of generating the observed data.



When a field of bioinformatics is mature, it becomes statistics.
E.g. Maximum-likelihood phylogenetics, HMMER, DESeq2, etc.

VDJ rearrangement


HMM intro: dishonest casino

HMM intro: dishonest casino

HMM intro: dishonest casino

HMM intro: dishonest casino

  1. What is the likelihood of the data under this path (write equation)
  2. If \(p\) is close to 0.5, what is an alternate path that will have a higher likelihood? What is this likelihood?

Biased die roll \(\leftrightarrow\) read base (under mutation)
Switching dice \(\leftrightarrow\) changing between V, D, J genes

 

VDJ annotation problem: from where did each nucleotide come?

A: Take maximum-likelihood HMM path.

What are probabilities?

Distributions are reproducibly weird!

Distributions are reproducibly weird!

Distributions are reproducibly weird!

Find clonal families

Find clonal families

Did two sequences come from the same VDJ recombination?

Say we are given two sequences

Double roll \(\leftrightarrow\) Pair HMM

Double roll \(\leftrightarrow\) Pair HMM



Pick double roll hypothesis if it has higher likelihood of generating data.


What about BCRs?


(But we only know the sequences, not the annotations!)

Do two sequences come from a single rearrangement event?

Probability of generating observed sequence \(x\) from HMM:

\[ \mathbb P(x) = \sum_{\text{paths}\ \sigma} \mathbb P(x;\sigma), \]

Probability of generating two sequences \(x\) and \(y\) from the same path through the HMM (i.e. from the same rearrangement event):

\[ \mathbb P(x,y) = \sum_{\text{paths}\ \sigma} \mathbb P(x,y;\sigma), \]

\[ \text{Calculate: } \frac{\mathbb P(x, y)}{\mathbb P(x) \mathbb P(y)} = \frac{\mathbb P(\text{single rearrangement})}{\mathbb P(\text{independent rearrangements})} \]

Do sets of sequences come from a
single rearrangement event?

 

\[ \frac{\mathbb P(A \cup B)}{\mathbb P(A) \mathbb P(B)} = \frac{\mathbb P(A \cup B \ | \ \text{single rearrangement})}{\mathbb P(A,B \ | \ \text{independent rearrangements})} \]

 

Use this for agglomerative clustering; stop when the ratio < 1.

  • Munshaw, S., & Kepler, T. B. (2010). SoDA2: a Hidden Markov Model approach for identification of immunoglobulin rearrangements. Bioinformatics.
  • Murugan, Mora, Walczak, & Callan (2012). Statistical inference of the generation probability of T-cell receptors from sequence repertoires. PNAS.
  • Ralph & M. (2016). Consistency of VDJ Rearrangement and Substitution Parameters Enables Accurate B Cell Receptor Sequence Annotation. PLOS Computational Biology.
  • Ralph & M. (2016). Likelihood-based inference of B-cell clonal families.PLOS Computational Biology.
  • Elhanati, Sethna, Marcou, Callan, Mora, \& Walczak (2015). Inferring processes underlying B-cell repertoire diversity. Philosophical Transactions of the Royal Society of London.
  • Elhanati, Marcou, Mora, & Walczak (2016). repgenHMM: a dynamic programming tool to infer the rules of immune receptor generation from sequence data. Bioinformatics.